回归
参考来源于2020台湾大学李宏毅课程和PPT
问题的导入:预测宝可梦的CP值
根据已有的宝可梦进化前后的信息,来预测某只宝可梦进化后的cp值的大小
supervised
设定具体参数
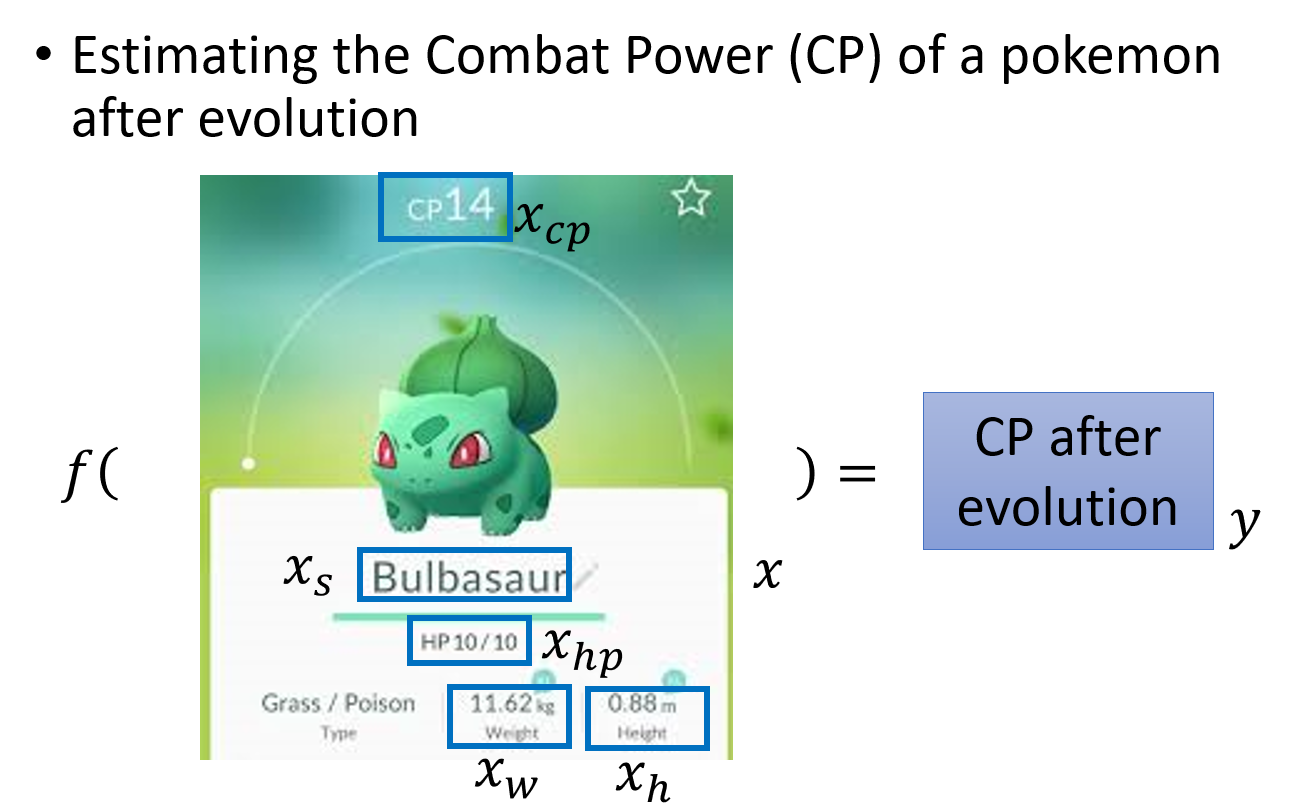
X X X: 表示一只宝可梦,用下标表示该宝可梦的某种属性
X c p X_{cp} Xcp:表示该宝可梦进化前的cp值
X s X_s Xs: 表示该宝可梦是属于哪一种物种,比如妙瓜种子、皮卡丘…
X h p X_{hp} Xhp:表示该宝可梦的hp值即生命值是多少
X w X_w Xw: 代表该宝可梦的重重量
X h X_h Xh: 代表该宝可梦的高度
f ( ) f() f(): 表示我们要找的function
y y y: 表示function的output,即宝可梦进化后的cp值,是一个scalar
Regression的具体过程
回顾一下machine Learning的三个步骤:
- 定义一个model即function set
- 定义一个goodness of function损失函数去评估该function的好坏
- 找一个最好的function
Step1:Model (function set)
如何选择一个function的模型呢?毕竟只有确定了模型才能调参。这里没有明确的思路,只能凭经验去一种种地试
Linear Model 线性模型
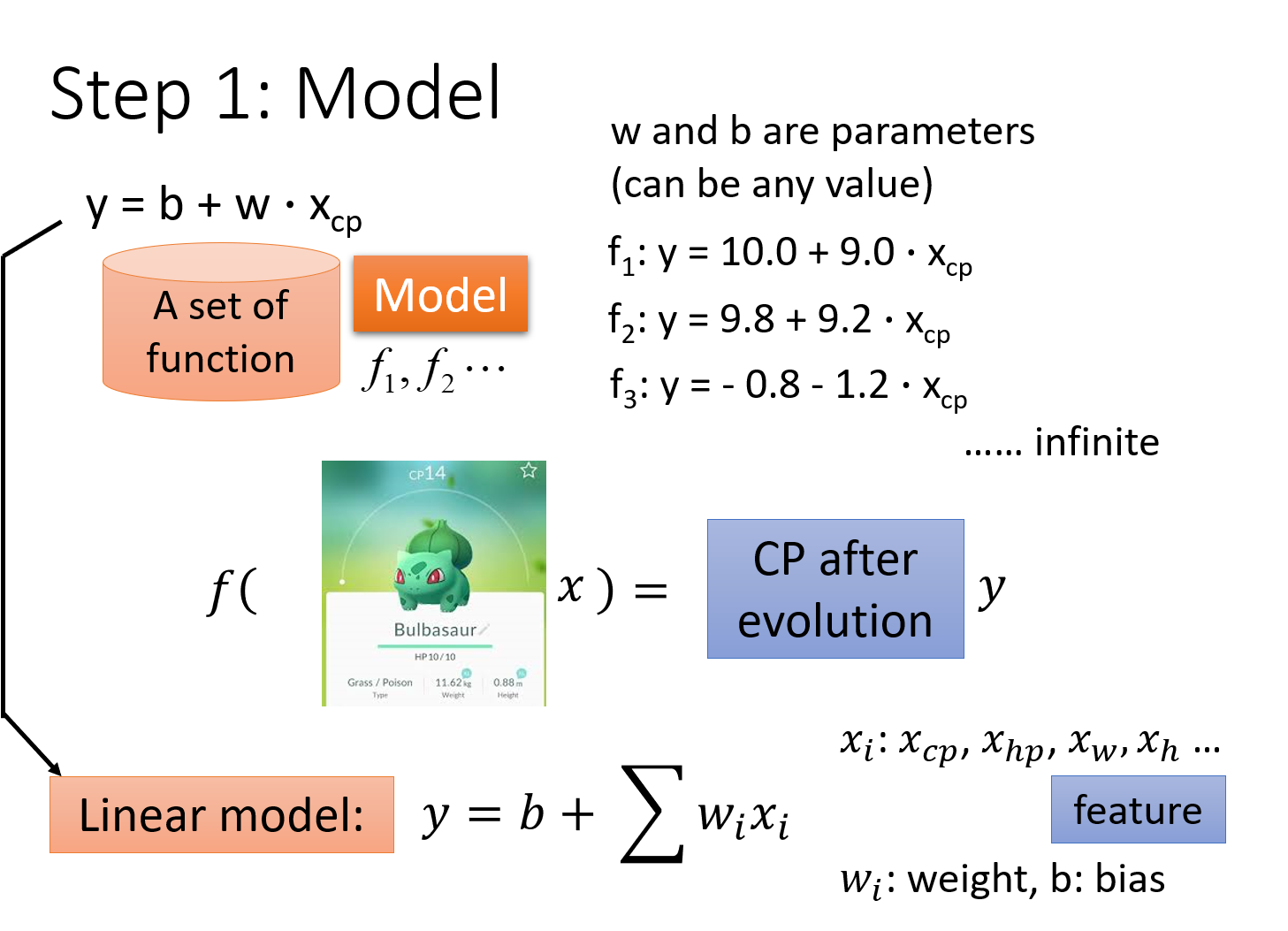
y = b + w ⋅ X c p y=b+w \cdot X_{cp} y=b+w⋅Xcp
y代表进化后的cp值, X c p X_{cp} Xcp代表进化前的cp值,w和b代表未知参数,可以是任何数值
根据不同的w和b,可以确定不同的无穷无尽的function,而 y = b + w ⋅ X c p y=b+w \cdot X_{cp} y=b+w⋅Xcp这个抽象出来的式子就叫做model,是以上这些具体化的function的集合,即function set
实际上这是一种Linear Model,但只考虑了宝可梦进化前的cp值,因而我们可以将其扩展为:
y = b + ∑ w i x i y=b+ \sum w_ix_i y=b+∑wixi
xi: an attribute of input X ( xi is also called feature,即特征值)
wi:weight of xi
b: bias
Step2:Goodness of Function
参数说明
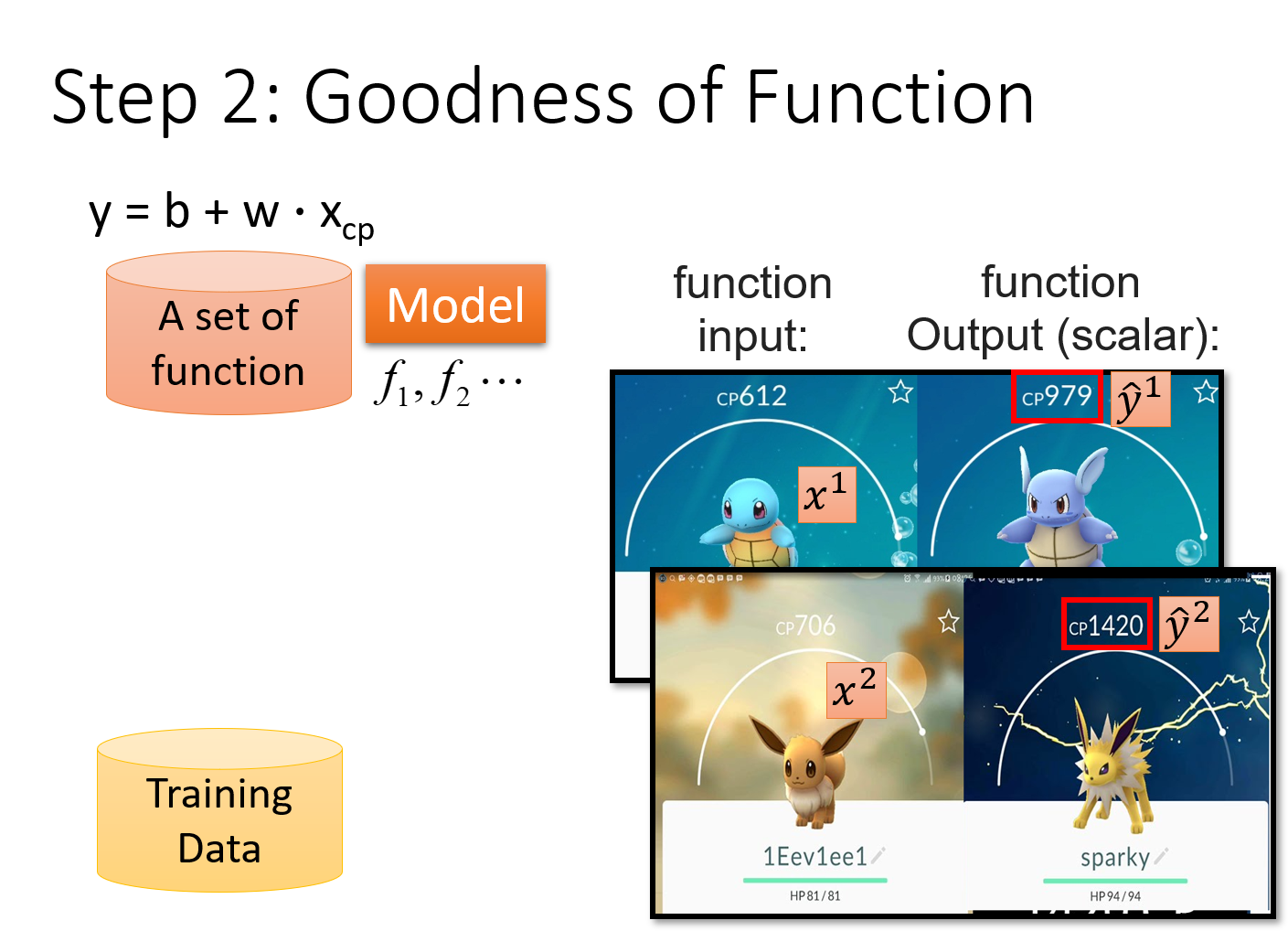
x i x^i xi:用上标来表示一个完整的object的编号, x i x^{i} xi表示第i只宝可梦(下标表示该object中的component)
y ^ i \widehat{y}^i y i:用 y ^ \widehat{y} y 表示一个实际观察到的object输出,上标为i表示是第i个object
注:由于regression的输出值是scalar,因此 y ^ \widehat{y} y 里面并没有component,只是一个简单的数值;但是未来如果考虑structured Learning的时候,我们output的object可能是有structured的,所以我们还是会需要用上标下标来表示一个完整的output的object和它包含的component
Loss function 损失函数
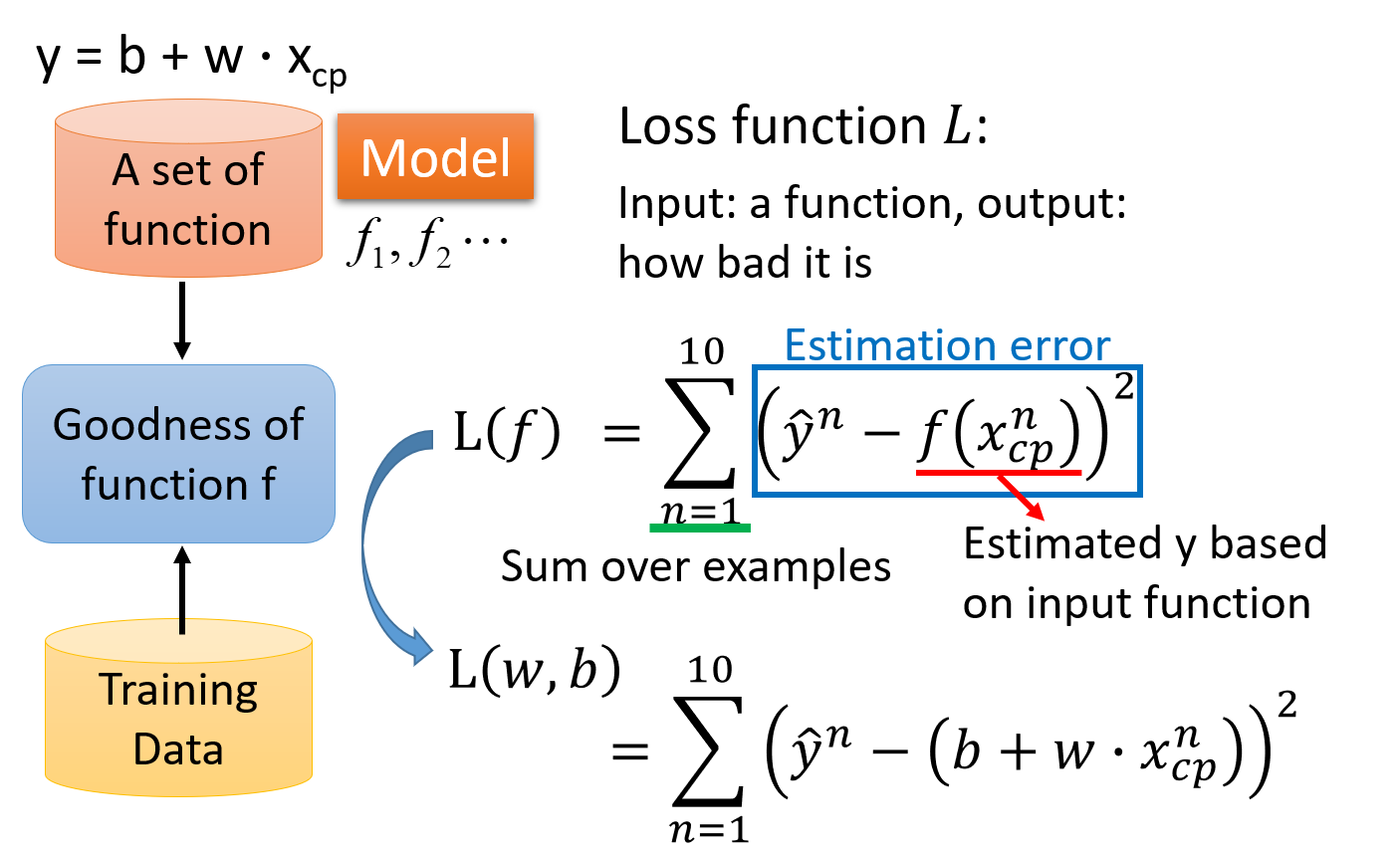
为了衡量function set中的某个function的好坏,我们需要一个评估函数,即Loss function,损失函数,简称L;loss function是一个function的function
L ( f ) = L ( w , b ) L(f)=L(w,b) L(f)=L(w,b)
input:a function;
output:how bad/good it is
由于 f : y = b + w ⋅ x c p f:y=b+w \cdot x_{cp} f:y=b+w⋅xcp,即f是由b和w决定的,因此input f就等价于input这个f里的b和w,因此Loss function实际上是在衡量一组参数的好坏
之前提到的model是由我们自主选择的,这里的loss function也是,最常用的方法就是采用类似于方差和的形式来衡量参数的好坏,即预测值与真值差的平方和;这里真正的数值减估测数值的平方,叫做估测误差,Estimation error,将10个估测误差合起来就是loss function
L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L(f)=L(w,b)=\sum_{n=1}^{10}(\widehat{y}^n-(b+w \cdot {x}^n_{cp}))^2 L(f)=L(w,b)=n=1∑10(y n−(b+w⋅xcpn))2
如果 L ( f ) L(f) L(f)越大,说明该function表现得越不好; L ( f ) L(f) L(f)越小,说明该function表现得越好
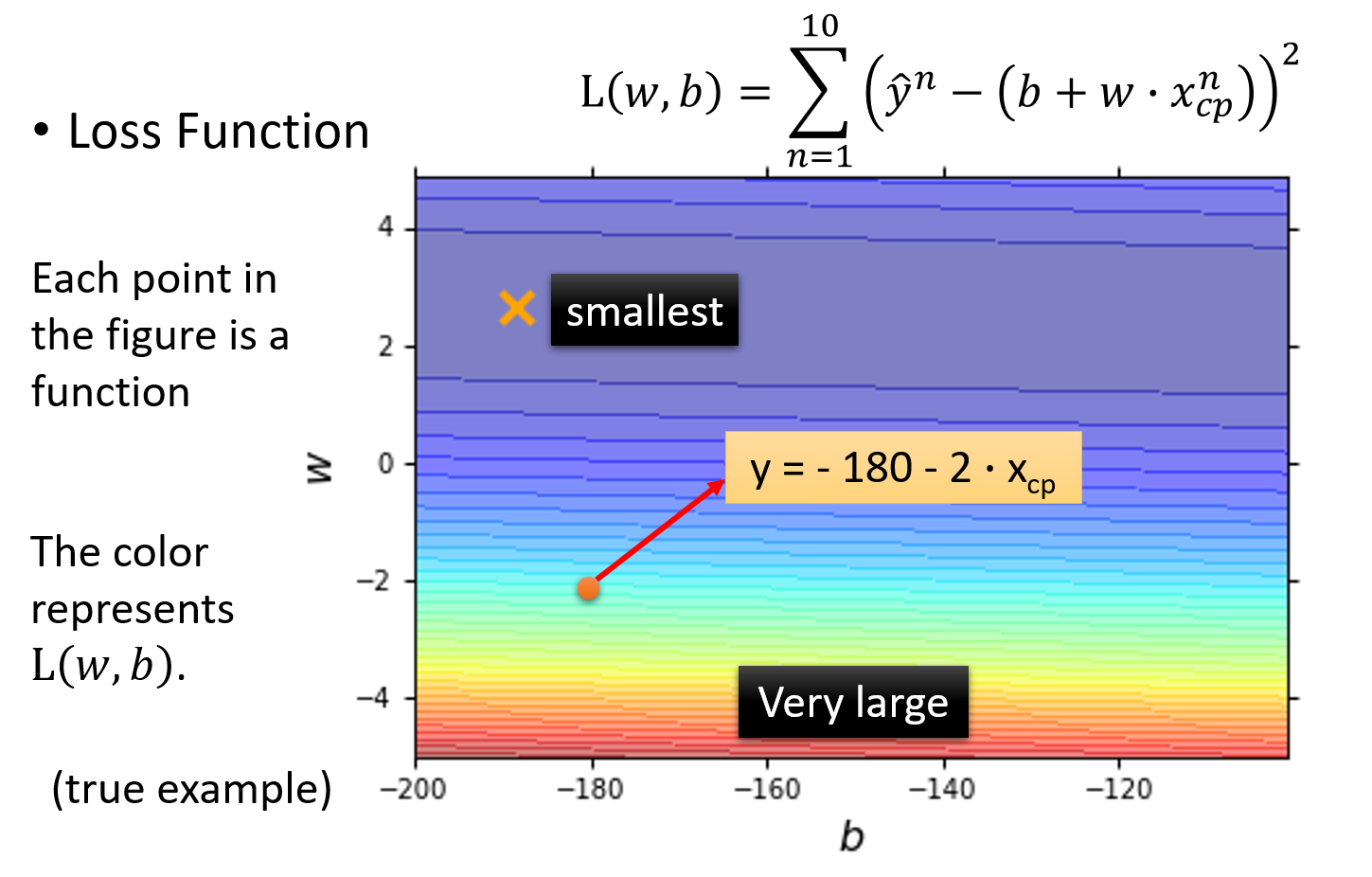
Loss function可视化
下图中是loss function的可视化,该图中的每一个点都代表一组(w,b),也就是对应着一个function;而该点的颜色对应着的loss function的结果L(w,b),它表示该点对应function的表现有多糟糕,颜色越偏红色代表Loss的数值越大,这个function的表现越不好,越偏蓝色代表Loss的数值越小,这个function的表现越好
比如图中用红色箭头标注的点就代表了b=-180 , w=-2对应的function,即 y = − 180 − 2 ⋅ x c p y=-180-2 \cdot x_{cp} y=−180−2⋅xcp,该点所在的颜色偏向于红色区域,因此这个function的loss比较大,表现并不好
Step3:Pick the Best Function
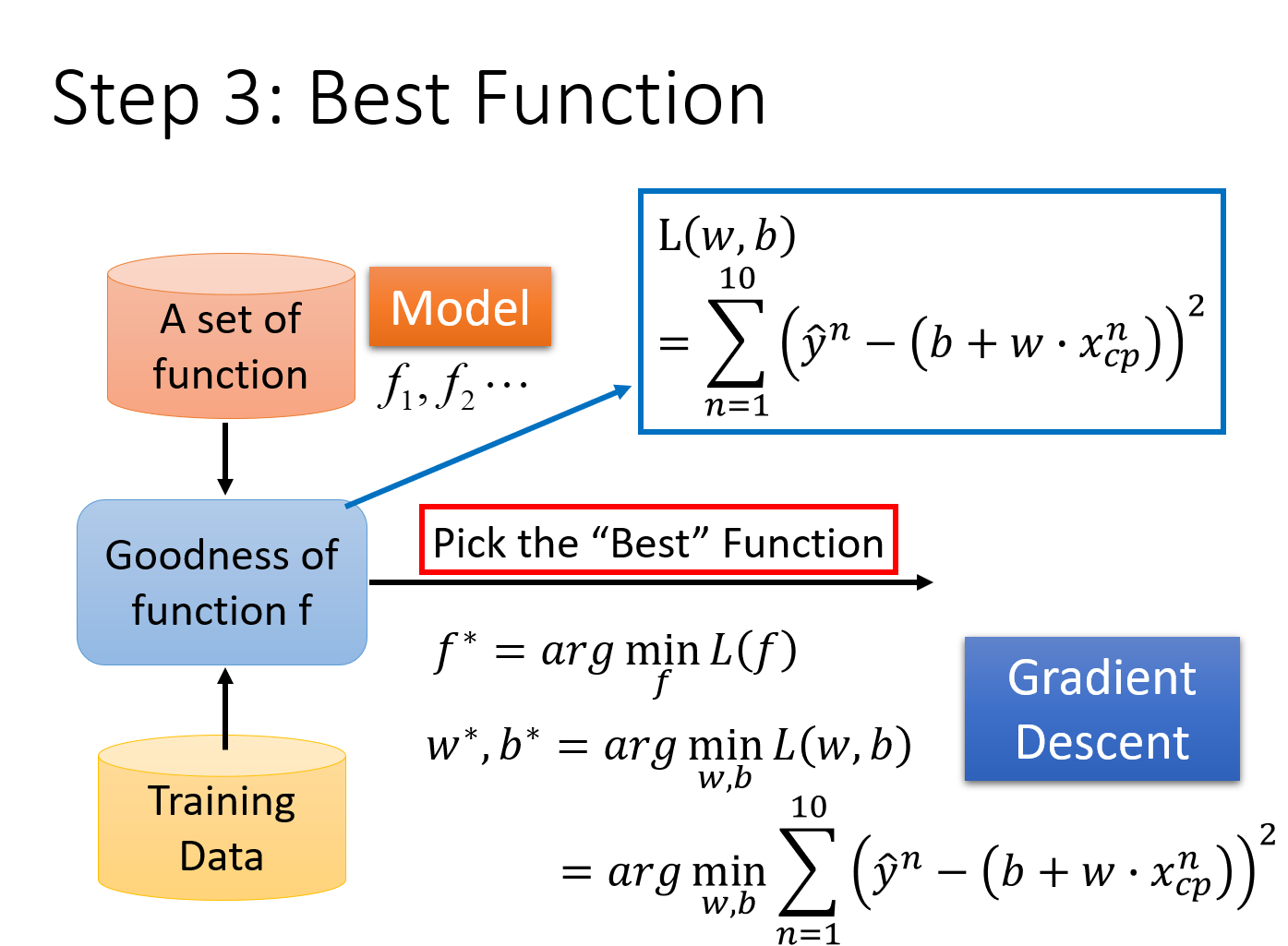
我们已经确定了loss function,他可以衡量我们的model里面每一个function的好坏,接下来我们要做的事情就是,从这个function set里面,挑选一个最好的function
挑选最好的function这一件事情,写成formulation/equation的样子如下:
f ∗ = a r g m i n f L ( f ) f^*={arg} \underset{f}{min} L(f) f∗=argfminL(f),或者是
w ∗ , b ∗ = a r g m i n w , b L ( w , b ) = a r g m i n w , b ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 w^*,b^*={arg}\ \underset{w,b}{min} L(w,b)={arg}\ \underset{w,b}{min} \sum\limits^{10}_{n=1}(\widehat{y}^n-(b+w \cdot x^n_{cp}))^2 w∗,b∗=arg w,bminL(w,b)=arg w,bminn=1∑10(y n−(b+w⋅xcpn))2
也就是那个使 L ( f ) = L ( w , b ) = L o s s L(f)=L(w,b)=Loss L(f)=L(w,b)=Loss最小的 f f f或 ( w , b ) (w,b) (w,b),就是我们要找的 f ∗ f^* f∗或 ( w ∗ , b ∗ ) (w^*,b^*) (w∗,b∗)(有点像极大似然估计的思想)
利用线性代数的知识,可以解得这个closed-form solution,但这里采用的是一种更为普遍的方法——gradient descent(梯度下降法)
Gradient Descent 梯度下降
上面的例子比较简单,用线性代数的知识就可以解;但是对于更普遍的问题来说,gradient descent的厉害之处在于,只要 L ( f ) L(f) L(f)是可微分的,gradient descent都可以拿来处理这个 f f f,找到表现比较好的parameters
单个参数的问题
以只带单个参数w的Loss Function L(w)为例,首先保证 L ( w ) L(w) L(w)是可微的
w ∗ = a r g m i n w L ( w ) w^*={arg}\ \underset{w}{min} L(w) w∗=arg wminL(w) 我们的目标就是找到这个使Loss最小的 w ∗ w^* w∗,实际上就是寻找切线L斜率为0的global minima最小值点(注意,存在一些local minima极小值点,其斜率也是0)
有一个暴力的方法是,穷举所有的w值,去找到使loss最小的 w ∗ w^* w∗,但是这样做是没有效率的;而gradient descent就是用来解决这个效率问题的
-
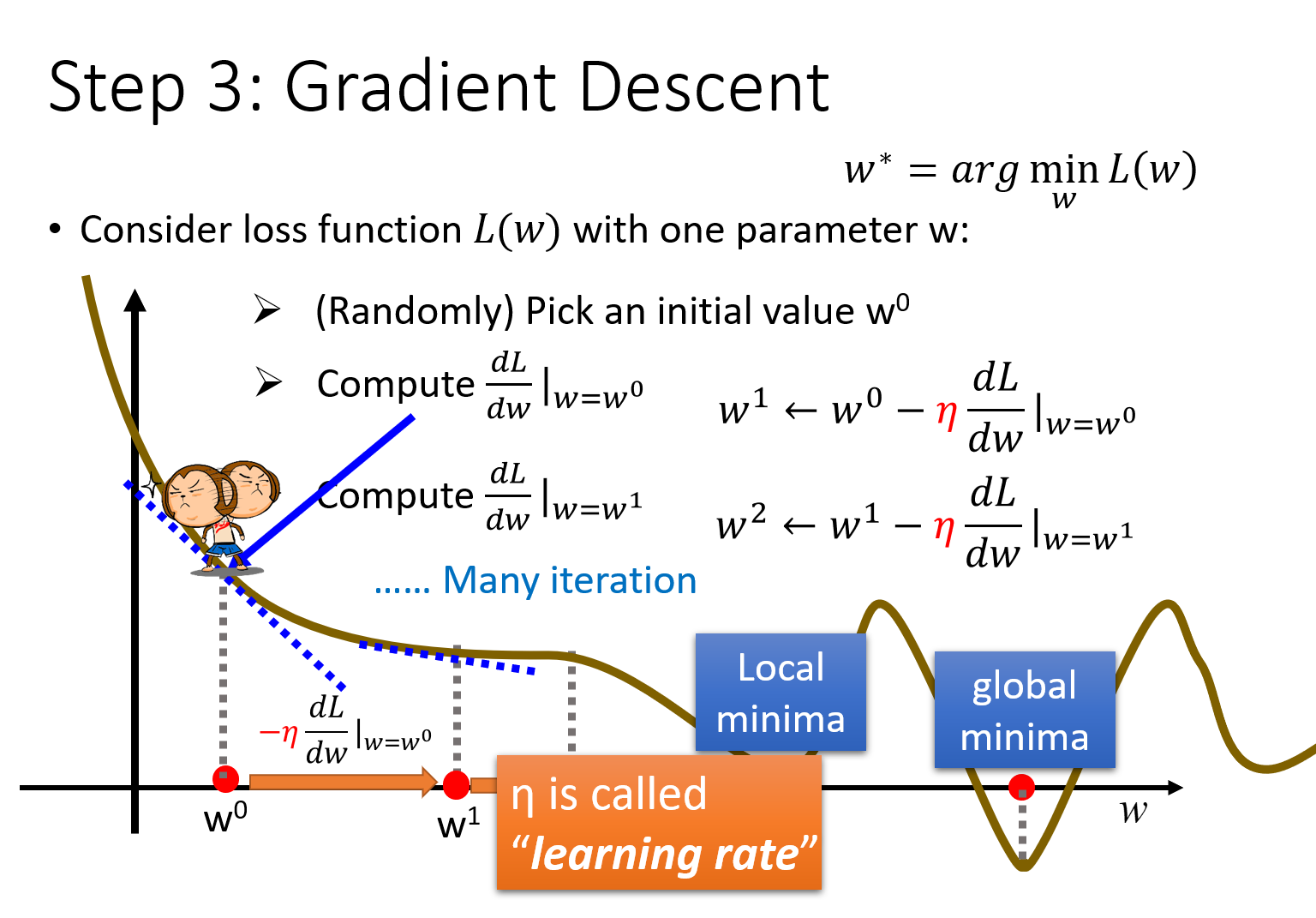
首先随机选取一个初始的点 w 0 w^0 w0 (当然也不一定要随机选取,如果有办法可以得到比较接近 w ∗ w^* w∗的表现得比较好的 w 0 w^0 w0当初始点,可以有效地提高查找 w ∗ w^* w∗的效率)
-
计算 L L L在 w = w 0 w=w^0 w=w0的位置的微分,即 d L d w ∣ w = w 0 \frac{dL}{dw}|_{w=w^0} dwdL∣w=w0,几何意义就是切线的斜率
-
如果切线斜率是negative负的,那么就应该使w变大,即往右踏一步;如果切线斜率是positive正的,那么就应该使w变小,即往左踏一步,每一步的步长step size就是w的改变量
w的改变量step size的大小取决于两件事
-
一是现在的微分值 d L d w \frac{dL}{dw} dwdL有多大,微分值越大代表现在在一个越陡峭的地方,那它要移动的距离就越大,反之就越小;
-
二是一个常数项 η η η,被称为learning rate,即学习率,它决定了每次踏出的step size不只取决于现在的斜率,还取决于一个事先就定好的数值,如果learning rate比较大,那每踏出一步的时候,参数w更新的幅度就比较大,反之参数更新的幅度就比较小
如果learning rate设置的大一些,那机器学习的速度就会比较快;但是learning rate如果太大,可能就会跳过最合适的global minima的点
-
-
因此每次参数更新的大小是 η d L d w η \frac{dL}{dw} ηdwdL,为了满足斜率为负时w变大,斜率为正时w变小,应当使原来的w减去更新的数值,即
w 1 = w 0 − η d L d w ∣ w = w 0 w 2 = w 1 − η d L d w ∣ w = w 1 w 3 = w 2 − η d L d w ∣ w = w 2 . . . w i + 1 = w i − η d L d w ∣ w = w i i f ( d L d w ∣ w = w i = = 0 ) t h e n s t o p ; w^1=w^0-η \frac{dL}{dw}|_{w=w^0} \\ w^2=w^1-η \frac{dL}{dw}|_{w=w^1} \\ w^3=w^2-η \frac{dL}{dw}|_{w=w^2} \\ ... \\ w^{i+1}=w^i-η \frac{dL}{dw}|_{w=w^i} \\ if\ \ (\frac{dL}{dw}|_{w=w^i}==0) \ \ then \ \ stop; w1=w0−ηdwdL∣w=w0w2=w1−ηdwdL∣w=w1w3=w2−ηdwdL∣w=w2...wi+1=wi−ηdwdL∣w=wiif (dwdL∣w=wi==0) then stop;
此时 w i w^i wi对应的斜率为0,我们找到了一个极小值local minima,这就出现了一个问题,当微分为0的时候,参数就会一直卡在这个点上没有办法再更新了,因此通过gradient descent找出来的solution其实并不是最佳解global minima但幸运的是,在linear regression上,是没有local minima的,因此可以使用这个方法
两个参数的问题
今天要解决的关于宝可梦的问题,是含有two parameters的问题,即 ( w ∗ , b ∗ ) = a r g m i n w , b L ( w , b ) (w^*,b^*)=arg\ \underset{w,b} {min} L(w,b) (








 本文通过预测宝可梦的CP值来介绍机器学习中的回归问题,详细讲解了线性模型、损失函数、梯度下降法,并通过实际例子探讨了模型复杂度、过拟合与正则化的关系。在梯度下降过程中,讨论了单参数和多参数的优化,并分析了不同模型在训练数据和测试数据上的误差表现,强调了模型选择的重要性。
本文通过预测宝可梦的CP值来介绍机器学习中的回归问题,详细讲解了线性模型、损失函数、梯度下降法,并通过实际例子探讨了模型复杂度、过拟合与正则化的关系。在梯度下降过程中,讨论了单参数和多参数的优化,并分析了不同模型在训练数据和测试数据上的误差表现,强调了模型选择的重要性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 932
932

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








