Bayesian Rose Trees 贝叶斯玫瑰树

Bayesian Rose Trees 贝叶斯玫瑰树

详细内容见论文原文，本文仅供交流学习使用，如有错误请指正。  

论文地址：Bayesian Rose Trees
Python 实例：贝叶斯层次聚类和贝叶斯玫瑰树

背景

  大多数层次聚类算法采用二叉树表示数据，其中叶子节点对应数据点，内部节点对应集群。但是在许多情况下，假设空间仅仅局限于二叉树是不可取的。首先，现实世界中许多的层次结构并不是二进制的。其次，将算法限制在二叉树上，往往会导致虚假的结构，从而使从业者解释树的时候产生误解。这些算法也不会返回解释数据最简单的结构，因为他们已经被排除在假设空间之外。
  下图展示了贝叶斯层次聚类（BHC）返回这种虚假结构的例子。

贝叶斯层次聚类（左）贝叶斯玫瑰树（右）

在这种情况下，级联表示三个大型集群，二叉树不能正确地表示数据中的大簇。理想情况下，树结构应该将每个级联折叠为一个节点，其中包含多个节点，表示子节点之间的区别。贝叶斯玫瑰树扩大了层次聚类算法的假设空间，将每个内部节点上具有任意分支结构的树也包含在内。因为分支结构有更多的选择，所以玫瑰树的空间要比二叉树大，搜索好的树也更加困难。

玫瑰树定义

  玫瑰树 $T$ 是递归定义的：对于数据点$x$，$T=x$ 或者 $T=T_1,...,T_{n_T}$ 其中$T_i$ 是不相交的数据点集合上的玫瑰树。在后者中，$T_i$ 是 $T$ 的子元素，$T$ 有 $n_T$个子元素。设叶节点 $(T)$ 是在 $T$ 的叶节点上的数据点集合。
  分区和分区结合体的概念是二叉树情况的直接推广。用 “ | ” 表示分区，例如 $ab|c$ 表示将集合 $a,b,c$ 划分成不相交的子集 $a,b$ 和 $c$。用玫瑰树 $T$ 表示某些数据点 $D$ 所有分区的结构化子集 $P(T)$。具体的可以递归定义如下：

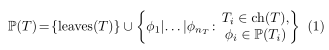
其中 $ch(T)$ 是 $T$ 的子节点，$leaves(T)$ 表示在 $T$ 的叶子节点上所有数据点聚集的分区。粗略说，每个分区从树根开始，将子叶保留在一个簇中或者划分到子树中。在每个子树上重复这个过程。最终结果是 $\varphi \in P(T)$ 由不重叠的簇组成，每个簇由T中的某一子树的所有叶组成。用 $fron{t}_T(\varphi )$ 来表示这些子树，用 $a{n}_T(\varphi )$ 来表示祖先集。

  作者将一棵玫瑰树 $T$ 解释为 $P(T)$ 中叶子节点 $D$ 的数据点的分区结合体：

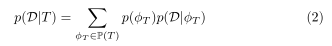
$p({\varphi }_T)$表示分区 ${\varphi }_T$ 的混合比例，$p(D|{\varphi }_T)$为数 $D$ 按 ${\varphi }_T$ 进行分区的概率。由于分区数量可能是指数级的，为了便于计算，作者定义了一个混合模型，使 $p(D|T)$ 可以使用对 $T$ 的动态规划来进行计算：

$f(D)$ 是数据 $D$ 在指数族下的边际概率，其中的参数在超参数 $\beta$ 的共轭先验下被边缘化，${\pi }_T$ 是混合比例。比较（2）（3）可得：

$D$ 在分区 ${\varphi }_T$ 下的概率就是指数族中 ${\varphi }_T$ 的数据点的每个簇 $D$` 的概率。${\pi }_T$ 表示 $T$ 下的叶子被保留在一个簇中而不是被递归分区过程细分的优先概率。${\pi }_T$ 定义如下：

$0\le \gamma \le 1$ 是模型超参数，控制数据的粗分区与细分区的相对比例。当限制于二叉树时，${\pi }_T=\gamma$。

  综上，玫瑰树下 $T$ 的 $D$ 的边际概率 $p(D|T)$ 是一个与 $T$ 保持一致的分区结合，其中 $D$ 在 $\varphi \in p(T)$ 的一个分区下的概率 ${\prod }_{D\in \varphi }f(D)$ 是 $\varphi$ 中簇的概率的乘积。

避免不必要级联

两棵玫瑰树

  考虑图中数据点 $D$（由a，b，c，d组成）上的两棵玫瑰树。假设a，b，c彼此相似，在其它方面有所区分，应该在一个簇中，但是与d不同。所以应该更倾向于玫瑰树 $R$ 。图中还显示了 $B$ 在 BHC-$\gamma$下的分区及其混合比例，以及R在BRT下的分区及其混合比例。因为数据点a，b，c属于一个簇，我们期望在分区下数据的边际似然（ $p(D|\varphi )={\prod }_{D\in \varphi }f(D)$ 是分区 $\varphi$ 的似然）存在以下不等式：

我们期望在可能的情况下模型更倾向于R而不是B，于是需要有:

将R和B下的边际似然扩展为每个分区下的似然的混合.如果我们设有a，b，c的子树R的混合比例 ${\pi }_{abc}$ 为 $1-{\pi }_{abc}=(1-\gamma {)}^2$ 利用个分区似然之间的不等式，可以保证（10）。于是 $B$ 中大量分区被丢弃重新分配至 $R$ 中的折叠分区。

贝叶斯玫瑰混合树的贪婪构造

  采用模型选择的方法来寻找给定数据的玫瑰树结构。理想情况下，我们希望找到一棵玫瑰树 $T^{\ast }$ 最大化数据 $D$ 的边际概率。

  因为存在成指数级数量的玫瑰树，于是采用以下贪婪聚集法构造玫瑰树。最初，每个数据点 $x_i$ 都被分配给它自己的玫瑰树： T i = { x i } T_i=\{x_i\} Ti​={xi​}。每一步选取两棵玫瑰树 $T_i$ 和 $T_j$，将它们合并为一棵树 $T_m$。不断重复这个过程，直到只剩下一棵树。
  为了允许每个节点拥有超过两个孩子，作者考虑了三种合并类型如下图：

  每一步算法选择一对树以及四种可能的合并操作（吸收存在两种可能）。选择的树对和合并操作是最大似然比的组合：

算法伪代码如下：

与 BHC-$\gamma$ 的分层结构比较

数据集来自Cree和McRae(2003)，由60个对象组成，每个对象都有100个二进制属性

  这幅图显示了BRT不仅发现比BHC-$\gamma$更简单、更容易解释层次结构，而且更可能解释数据。