CF1450C - Errich-Tac-Toe——构造

最新推荐文章于 2022-03-21 15:19:34 发布

偶耶XJX

最新推荐文章于 2022-03-21 15:19:34 发布

阅读量393

点赞数

分类专栏：信息竞赛解题文章标签： Codeforces 构造

本文链接：https://blog.csdn.net/weixin_43960287/article/details/118694546

版权

信息竞赛解题专栏收录该内容

195 篇文章 5 订阅

订阅专栏

C - Errich-Tac-Toe

题目描述

给定n*n大小的网格，每个格子内图形为.，O或X，O和X的总个数为k。

你需要在最多 $\lfloor\frac{k}{3}\rfloor$ 次操作（把O变为X或把X变为O）后，使得网格中每一行和每一列都不存在连续三个O或X。

数据范围与提示

$1\le n\le 300$ 。

前言

我连C题都不会。

思路

首先来想Easy Version：显然如果每两个斜排（行标加列标相等的为一个斜排）的X后面出现一个斜排的O，那么一定可以把行和列上所有可能的连续三个X都断开。

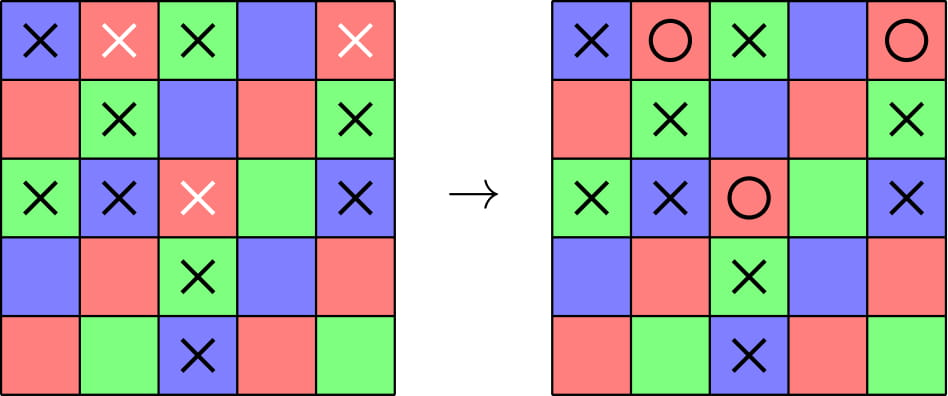
官解的图片

（骠的官方的图）红色的斜排上的X全变为O以断开三连的X。

我们设 $a_i$ 表示所有满足行标加列标的和取模3等于 $i$ 的X的个数，显然 $a_0+a_1+a_2=k$ ，所以 $\min(a_0,a_1,a_2)\le \lfloor\frac{k}{3}\rfloor$ ，选X的个数最小的方案涂O一定可以满足要求。

然后想想怎么扩展到Hard Version。

显然每三个斜排里面需要有一排全O来断开X，还需要有一排全X来断开O。

同理，我们设 $c_{ij}$ ， $i,j=0/1/2$ 表示%3为 $i$ 的斜排全部涂O，%3为 $j$ 的斜排全部涂X的情况下的操作次数，同时再设 $b_i$ 表示所有满足行标加列标的和取模3等于 $i$ 的O的个数，那么有 $c_{ij}=a_i+b_j$ ， $c_{01}+c_{02}+c_{10}+c_{12}+c_{20}+c_{21}=2k$ ，所以 $\min(c_{01},c_{02},c_{10},c_{12},c_{20},c_{21})=\lfloor\frac{2k}{6}\rfloor=\lfloor\frac{k}{3}\rfloor$ ，还是选操作最少的方案。

当然，有不少更复杂的乱搞做法也把正解的构造搞出来了，由于本质相同，故不提。

代码

我就只贴Hard Version的代码好了。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<string>
#include<map>
#include<ctime>
#define ll long long
#define MAXN 305
#define uns unsigned
#define MOD 998244353ll
#define INF 0x3f3f3f3f
#define lowbit(x) ((x)&(-(x)))
using namespace std;
inline ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+s-'0',s=getchar();
	return f?x:-x;
}
int n,n1[3],n2[3],zt[3];
char s[MAXN][MAXN];
signed main()
{
	for(int T=read();T--;){
		n=read();
		for(int i=0;i<3;i++)n1[i]=n2[i]=zt[i]=0;
		for(int i=1;i<=n;i++){
			scanf("%s",s[i]+1);
			for(int j=1;j<=n;j++){
				if(s[i][j]=='O')n1[(i+j)%3]++;
				else if(s[i][j]=='X')n2[(i+j)%3]++;
			}
		}
		int u=0,v=1;
		for(int i=0;i<3;i++)
			for(int j=0;j<3;j++)
				if(i!=j&&n2[i]+n1[j]<n2[u]+n1[v])u=i,v=j;
		zt[u]=1,zt[v]=2;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(s[i][j]=='X'&&zt[(i+j)%3]==1)s[i][j]='O';
				else if(s[i][j]=='O'&&zt[(i+j)%3]==2)s[i][j]='X';
				putchar(s[i][j]);
			}
			putchar('\n');
		}
	}
	return 0;
}