[ZJOI2022] 简单题——圆方树、树链剖分

[ZJOI2022] 简单题

题解

先说是满足环长相等的，然后又任改边权？我寻思这不是没性质了吗？

哦，正整数边权啊，那没事了。

由于原来的边权是正整数，为了使得环长能够通过改边权变得相等，原图的每个点双连通分量一定长成“杨桃”形：

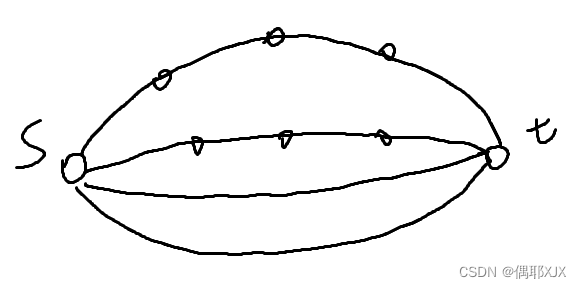
严格来说，每个点双内最多有两个点 $s$ 和 $t$ 度数大于2，其它点的度数都等于2（两个点的点双例外），相当于被 $s$ 和 $t$ 割成很多条链。

此时，点双内任意两点 $x,y$ 间的简单路径数量和长度和是可以快速求得的。
我们先做亿点预处理，求出每个点双内的 $s,t$、链数 $m$、每条链的长度 $lt[i]$，所有链的长度和 $sum$，以及每个点所在链的标号 $ne[x]$、每个点走自己那条链到 $s$ 的距离 $ds[x]$ 等，然后分情况讨论：

• $x=s,y=t$ 或 $x=t,y=s$：
  此时答案为 $(m,sum)$；（前一个是路径数量，后一个是路径长度和）
• $x$ 和 $y$ 的其中一个是 $s$ 或 $t$，另一个在链上：
  显然共有4种情况，求法都是一样的。我们以 $x=s$ 为例，此时路径要么直接走 $y$ 所在链到达 $y$，要么先走另一条链到 $t$，再走背面到 $y$，答案为 $(m,sum+(lt[ne[y]]-ds[y])\times (m-2))$；（这是化简后的结果）
• $x,y$ 在同一条链上：
  要么在链上直达，要么先走到 $s$ 或 $t$，再走另一条链，答案是 $(m,sum+(lt[ne[x]]-|ds[x]-ds[y]|)\times (m-2))$；
• $x,y$ 不在同一条链上：
  这个时候 $x$ 可以走 $s$，也可以走 $t$，而走到 $s$ 或 $t$ 过后就和第二种情况及其相似了，所以可以写出总共4种情况的答案的和：
  $$\begin{gathered} (2m-2,ds[x]+ds[y] \\ +(ds[x]+lt[ne[y]]-ds[y])\times (m-2)+sum-lt[ne[x]]-lt[ne[y]] \\ +lt[ne[x]]-ds[x]+lt[ne[y]]-ds[y] \\ +(ds[y]+lt[ne[x]]-ds[x])\times (m-2)+sum-lt[ne[x]]-lt[ne[y]]) \end{gathered}$$化简得到 $(2m-2,(lt[ne[x]]+lt[ne[y]])\times (m-3)+2sum)$。

适当使用unordered_map，预处理可以做到 $O(n)$，查询 $O(1)$。

然后对于不在一个点双内的点，我们可以建出广义圆方树，令圆点的点权为到它爷爷节点（同在父亲节点代表的点双内）的路径数和长度和，那么两点间的答案可由圆方树上路径上的圆点点权合并而来，只不过需要再特殊处理一下LCA。

用重链剖分可以比较省空间地做到 $O(\log n)$ 查询，只需要每个节点记录到链顶的答案的合并，然后对于中间的小段则做个逆变换除掉即可。

总复杂度是 $O(n\log n)$，O(n) 部分的常数比 log 大。

代码

#include<bits/stdc++.h>//JZM yyds!!
#define ll long long//God JZM!!
#define lll __int128//JZM RollInDark!!
#define uns unsigned
#define fi first
#define se second
#define IF (it->fi)
#define IS (it->se)
#define lowbit(x) ((x)&-(x))
#define END putchar('\n')
#define inline jzmyyds
#pragma GCC optimize("Ofast")
using namespace std;
const int MAXN=2e6+6;
const ll INF=1e18;
ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
int ptf[50],lpt;
void print(ll x,char c='\n'){
	if(x<0)putchar('-'),x=-x;
	ptf[lpt=1]=x%10;
	while(x>9)x/=10,ptf[++lpt]=x%10;
	while(lpt)putchar(ptf[lpt--]^48);
	if(c>0)putchar(c);
}

const ll MOD=998244353;
ll ksm(ll a,ll b,ll mo){
	ll res=1;if(a==1)return 1;
	for(;b;b>>=1,a=a*a%mo)if(b&1)res=res*a%mo;
	return res;
}
#define pii pair<int,int>
struct edge{
	int v,to,w;edge(){}
	edge(int V,int T,int W){v=V,to=T,w=W;}
}e[MAXN];
int EN,G[MAXN];
void addedge(int u,int v,int w){
	e[++EN]=edge(v,G[u],w),G[u]=EN;
	e[++EN]=edge(u,G[v],w),G[v]=EN;
}
pii del[MAXN];
int n,m,Q,dfn[MAXN],low[MAXN],TN,tot;
vector<int>D[MAXN];
void adge(int u,int v){
	D[u].push_back(v),D[v].push_back(u);
}

#define pll pair<ll,ll>
pll operator*(const pll&a,const pll&b){
	return pll(a.fi*b.fi%MOD,(a.fi*b.se+a.se*b.fi)%MOD);
}
pll operator/(const pll&a,const pll&b){
	ll iv=ksm(b.fi,MOD-2,MOD),f=a.fi*iv%MOD;
	return pll(f,(a.se-f*b.se%MOD+MOD)*iv%MOD);
}

struct{//点双
	int s,t,siz,m;ll sum;
	vector<int>p,ne;
	unordered_map<int,int>id;
	unordered_map<int,vector<pii> >G;
	vector<ll>ds,lt;
	void insp(int x){p.push_back(x),id[x]=233,siz++;}
	void inse(int u,int v,int w){
		if(u==v||!id.count(u)||!id.count(v))return;
		G[u].emplace_back(pii(v,w));
		G[v].emplace_back(pii(u,w));
	}
	void dfs(int x,int fa,int fd,int w){
		if(x==t){
			lt.emplace_back(ds[fd]+w);
			sum+=ds[fd]+w,m++;return;
		}int d=id[x];
		ne[d]=m,ds[d]=ds[fd]+w;
		for(auto&v:G[x])if(v.fi^fa)dfs(v.fi,x,d,v.se);
	}
	void build(){
		ne.resize(siz),ds.resize(siz);
		int mx=0;
		for(int i=0,x;i<siz;i++)
			x=p[i],id[x]=i,ne[i]=G[x].size(),mx=max(mx,ne[i]);
		s=t=m=0;
		for(int i=0;i<siz&&!t;i++)if(ne[i]==mx){
			if(!s)s=p[i];
			else t=p[i];
		}dfs(s,s,id[s],0);
	}
	pll cont(int x,int y){
		if(x==y||!id.count(x)||!id.count(y))return pll(1,0);
		int u=id[x],v=id[y];
		if(u>v)swap(x,y),swap(u,v);
		if(x==s){
			if(y==t)return pll(m,sum%MOD);
			return pll(m,(sum+(lt[ne[v]]-ds[v])%MOD*(m+MOD-2))%MOD);
		}
		if(x==t)return pll(m,(sum+ds[v]%MOD*(m+MOD-2))%MOD);
		if(y==s)return pll(m,(sum+(lt[ne[u]]-ds[u])%MOD*(m+MOD-2))%MOD);
		if(y==t)return pll(m,(sum+ds[u]%MOD*(m+MOD-2))%MOD);
		if(ne[u]==ne[v]){
			ll d=abs(ds[u]-ds[v]);
			return pll(m,(sum+(lt[ne[u]]-d)%MOD*(m+MOD-2))%MOD);
		}
		return pll((m-1)<<1,((lt[ne[u]]+lt[ne[v]])%MOD*(m+MOD-3)+(sum<<1))%MOD);
	}
}sc[MAXN];

int sk[MAXN],le,bl[MAXN];
void tarjan(int x,int fa){
	dfn[x]=low[x]=++TN,sk[++le]=x;
	for(int i=G[x],v;i;i=e[i].to){
		if((v=e[i].v)==fa)continue;
		if(dfn[v])low[x]=min(low[x],dfn[v]);
		else{
			tarjan(v,x),low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x]){
				tot++,sc[tot].insp(x),adge(x,n+tot);
				while(le>0){
					sc[tot].insp(sk[le]),bl[sk[le]]=tot,adge(sk[le--],n+tot);
					if(sk[le+1]==v)break;
				}
			}
		}
	}
}

int fa[MAXN],siz[MAXN],hs[MAXN],dep[MAXN],tp[MAXN];
pll a[MAXN],f[MAXN];
void dfs1(int x){
	siz[x]=1,hs[x]=0,a[x]=pll(1,0),dep[x]=dep[fa[x]]+1;
	for(int v:D[x])if(v^fa[x]){
		fa[v]=x,dfs1(v),siz[x]+=siz[v];
		if(siz[v]>siz[hs[x]])hs[x]=v;
	}
	if(x>n)for(int v:D[x])if(v^fa[x])a[v]=sc[x-n].cont(v,fa[x]);
}
void dfs2(int x){
	tp[x]=(x==hs[fa[x]]?tp[fa[x]]:x),f[x]=a[x];
	if(tp[x]^x)f[x]=f[x]*f[fa[x]];
	if(hs[x])dfs2(hs[x]);
	for(int v:D[x])if((v^fa[x])&&(v^hs[x]))dfs2(v);
}
ll query(int u,int v){
	int x=u,y=v;
	pll res=pll(1,0);
	while(tp[u]^tp[v]){
		if(dep[tp[u]]<dep[tp[v]])swap(u,v),swap(x,y);
		res=res*f[u],x=tp[u],u=fa[tp[u]];
	}if(dep[u]>dep[v])swap(u,v),swap(x,y);
	if(v^u)y=hs[u],res=res*f[v]/f[u];
	if(u>n)res=res*sc[u-n].cont(x,y)/a[x]/a[y];
	return res.se;
}
int main()
{
	freopen("simple.in","r",stdin);
	freopen("simple.out","w",stdout);
	n=read(),m=read(),Q=read();
	for(int i=1,u,v;i<=m;i++)
		u=read(),v=read(),addedge(u,v,read());
	tarjan(1,0);
	for(int i=1;i<=EN;i+=2){
		int u=e[i].v,v=e[i+1].v,w=e[i].w;
		if(bl[u]>0)sc[bl[u]].inse(u,v,w);
		if(bl[v]>0&&(bl[u]^bl[v]))sc[bl[v]].inse(u,v,w);
	}
	for(int i=1;i<=tot;i++)sc[i].build();
	dfs1(1),dfs2(1);
	while(Q--)print(query(read(),read()));
	return 0;
}