CF1261F Xor-Set （拆区间、扫描线）

DD(XYX)

于 2020-12-30 16:52:09 发布

阅读量141

点赞数 1

分类专栏：线段树

本文链接：https://blog.csdn.net/weixin_43960414/article/details/111657539

版权

线段树专栏收录该内容

53 篇文章 0 订阅

订阅专栏

题面

给出两个整数集合 $A, B$ ，
求所有使得存在 $a \in A, b \in B$ 且 $a \oplus b = c$ 的整数 $c$ 之和取模 $998244353$ 的值（所以说如果有多个 $a \oplus b$ 等于同一个 $c$ ，则该 $c$ 只计算一次贡献），
其中 $\oplus$ 表示按位异或，即 $x o r$ 。

对于 $A$ ，给出 $n_A$ ，
然后给出 $n_A$ 个区间 $l_i,r_i]$ ，表示对于所有满足 $l_i \le a \le r_i$ 的整数 $a$ 都有 $\in A$ （即 $[l_i,r_i] \in A$ ）。

对于 $B$ 以同样方式给出其中的元素。

$A, B$ 都是不重集，即每个整数至多在集合中出现一次（虽然对题意没有影响）。数据范围： $\le n_A,n_B \le 100,1 \le l_i,r_i \le 10^{18}$ 。

题解

~~这题好难啊做不来只好看题解了~~

首先肯定不能暴力两两异或，题解都是这么说的。

然后，可不可以区间与区间计算呢？可它是异或的嘛😕……

不过，我们发现还是有一些特殊的区间是可以两两计算的，

比如，形如 $L\,,\,L+2^k)$ （即 $L\,,\,L+2^k-1]$ ）的区间，其中满足 $L\;\&\;(2^k-1)==0$ ，或者也可以这样表示：
${ x \;|\; x \,\&\, (11...1111\,00...0)_2(k个0) == L, L\;\&\;(2^k-1)==0 \}$
（即前面固定，后面一段k位任意）

这样的两个区间计算结果怎样呢？

我们不妨设 $L_A,R_A]$ 长度更小，然后我们只讨论 60 个二进制位
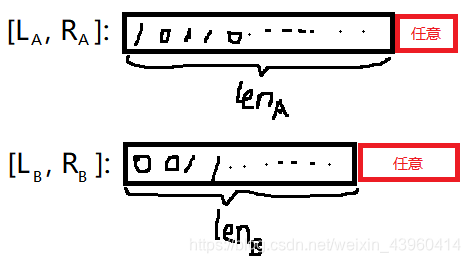
在这里插入图片描述
把它们异或起来，前面的 $len_B$ 位异或起来肯定是一个固定的值，
后面的 $60-len_B$ 位，由于 $L_B,R_B]$ 在这些位置是任意的(每一位不论取0或1最终的数都在这个区间中)，因此这些位置异或起来的答案也是任意的。
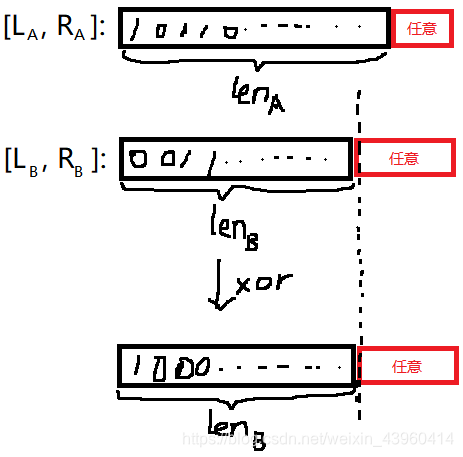
在这里插入图片描述
它们于是得到了一个连续的区间！！

所以我们考虑把 $A$ 的所有区间和 $B$ 的所有区间都拆成这样的特殊的区间，就可以计算了。

对于一个区间 $[L, R)$ ，我们可以把它拆成前面 $l o g$ 个区间：（注意开闭）
$[L,L+lowbit(L)\;)\;,\\ [L+lowbit(L),L+lowbit(L) + lowbit(L+lowbit(L))\;)\;,\\ ......$
加上后面 $l o g$ 个区间：
$......\\ [R-lowbit(R)-lowbit(R-lowbit(R)),R-lowbit(R)\;)\\ [R-lowbit(R),R\;)$

通过学习树状数组的经验，我们可以知道 $L$ 一直加 $l o w b i t (L)$ 、和 $R$ 一直减 $l o w b i t (R)$ 最终一定会相遇于一个数，所以证明了这 $2 l o g$ 个区间并起来是连续的、且恰好等于原区间 $[L, R)$ .

我们再看一下加lowbit的过程：
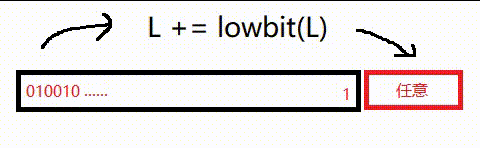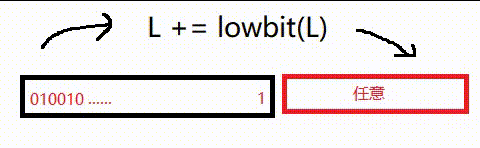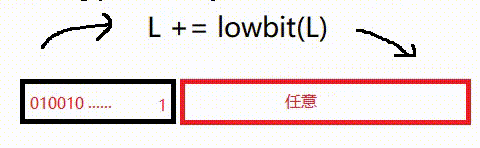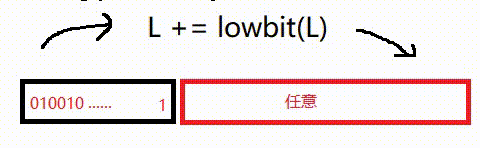
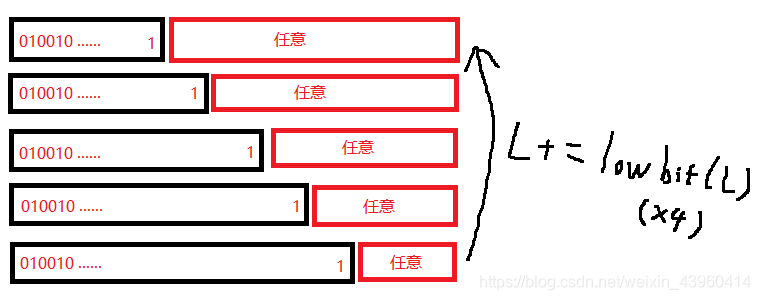
加lowbit的动态过程在这里插入图片描述
可以发现它开头的一段都没变，最多尾端的一个 0 变成了 1 ，

所以当B的一个新区间和A的一个原始区间 $[L, R)$ 计算时，
只需要分别和 $[L,L+lowbit(L)\;)$ 以及 $[R-lowbit(R),R\;)$ 计算，如果有的话，最多再加上一个和它一样长的区间。

然后再把 A，B 调转顺序跑一遍大的。

这样最终就只有 $n_A\!\!\cdot \!n_B\!\!\cdot \!log$ 个区间，
排个序，用扫描线，
按左端点排序，从左边扫，依次合并区间（区间并集），
若发现再合并上当前区间时会变得不连续，那么就把原先的区间的贡献计算了，然后变成空集和它合并，这应该很好理解吧 🙂

CODE

#include<queue>
#include<vector>
#include<cstdio>
#include<cstring> 
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 205
#define MAXM 4000005
#define LL long long
#define DB double
#define ENDL putchar('\n') 
#define MM(x) memset((x),0,sizeof((x)))
#define MAXI(x,y) ((x) = max((x),(y)))
#define MINI(x,y) ((x) = min((x),(y)))
#define lowbit(x) (-(x) & (x))
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return x * f;
}
const int MOD = 998244353;
const int inv2 = (MOD+1) / 2;
int n,m,i,j,s,o,k,cnc;
struct it{
	LL l,r;
	it(){l=r=0;}
	it(LL L,LL R){l=L;r=R;}
}A[MAXN],B[MAXN],a[MAXN<<1],b[MAXN<<1],c[MAXM];
bool cmp(it a,it b) {return a.l < b.l;}
void spli(it a,it *b,int &n) {
	n = 0;	
	LL ll = a.l,rr = a.r+1;
	for(LL i = ll;i+lowbit(i) <= rr;i += lowbit(i)) 
		b[++ n] = it(i,i+lowbit(i));
	for(LL i = rr;i-lowbit(i) >= ll;i -= lowbit(i)) 
		b[++ n] = it(i-lowbit(i),i);
	return sort(b + 1,b + 1 + n,cmp);
}
it merg(it a,it b) {
	LL x = max(a.r-a.l-1,b.r-b.l-1);
	it c; c.l = a.l ^ b.l; c.l = c.l - (c.l&x);
	c.r = c.l + x; return c;
}
int solve(LL l,LL r) {
	return (l + r) % MOD *1ll* ((r - l + 1) % MOD) % MOD *1ll* inv2 % MOD;
}
int main() {
	n = read();
	for(int i = 1;i <= n;i ++) {
		LL s = read(),o = read();A[i] = it(s,o);
	}
	m = read();
	for(int i = 1;i <= m;i ++) {
		LL s = read(),o = read();B[i] = it(s,o);
	}
	for(int i = 1;i <= n;i ++) {
		int la,lb;
		spli(A[i],a,la);
		for(int j = 1;j <= m;j ++) {
			spli(B[j],b,lb);
			for(int k = 1;k <= la;k ++) {
				if(a[k].r-a[k].l > b[1].r-b[1].l) c[++ cnc] = merg(a[k],b[1]);
				if(a[k].r-a[k].l > b[lb].r-b[lb].l) c[++ cnc] = merg(a[k],b[lb]);
				for(int l = 1;l <= lb;l ++) {
					if(a[k].r - a[k].l == b[l].r - b[l].l) {
						c[++ cnc] = merg(a[k],b[l]);
					}
				}
			}
			for(int k = 1;k <= lb;k ++) {
				if(b[k].r-b[k].l > a[1].r-a[1].l) c[++ cnc] = merg(b[k],a[1]);
				if(b[k].r-b[k].l > a[la].r-a[la].l) c[++ cnc] = merg(b[k],a[la]);
			}
		}
	}
	sort(c + 1,c + 1 + cnc,cmp);
	int ans = 0;
	LL ll = 0,rr = -1;
	for(int i = 1;i <= cnc;i ++) {
		if(c[i].l > rr) {
			(ans += solve(ll,rr)) %= MOD;
			ll = c[i].l; rr = c[i].r;
		}
		else rr = max(rr,c[i].r);
//		printf("[%lld,%lld]\n",c[i].l,c[i].r);
	}
	(ans += solve(ll,rr)) %= MOD;
	printf("%d\n",ans);
	return 0;
}