「2020.6.6多校省选模拟4」一道图论题（贪心，最大生成树）

题面

$$\begin{gathered} \text{最 简 单 题} \\ { \\ }_{{}_{\text{2000 ms 1024 MiB}}} \end{gathered}$$

你有两棵有根树$T_1,T_2$，这两棵树都有$n$个节点，并且$1$分别是这两棵树的根。这两棵树中，边都有边权，并且无向。

这两棵树的叶子个数相同，你需要把这两棵树的叶子进行匹配，也就是找到一个叶子之间的对应关系，$T_1$中的每个叶子唯一配对一个$T_2$中的叶子，然后将每对叶子缩成一个点，你可以认为在对应的叶子之间连上了一条边权为正无穷的边(注意这里不把$1$号点当作叶子)。

你想删除一些边，使得：

1. $T_1$和$T_2$的根节点不连通。
2. $T_1$和$T_2$的根所在的连通分量都是树。
3. $T_1$和$T_2$的根所在的连通分量的并集是全集，也就是每个点恰与$T_1$或$T_2$其中一个的根相连。

如果你最优地进行叶子匹配以及删边，问这些删除的边最小的边权和是多少。

输入格式

第一行一个整数$n$。

接下来$n-1$行，每行三个整数$u,v,w$表示$T_1$里面的一条边。

接下来$n-1$行，每行三个整数$u,v,w$表示$T_2$里面的一条边。

输出格式

一个整数表示答案

样例输入

5
1 2 1
1 5 3
2 3 4
2 4 6
1 2 8
1 3 7
2 4 2
2 5 5

样例输出

6

样例解释

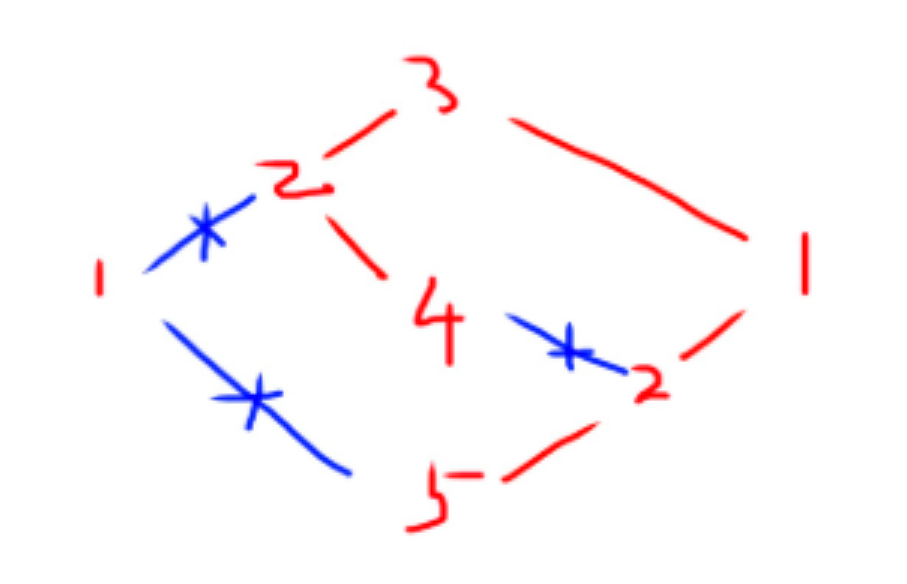
数据限制

$20\%$，$n\le 10$。

$50\%$，$n\le 200$。

$100\%$，$1\le n\le 10^5,1\le w\le 10^9$。

题解

如果我们已经确定了叶子的配对，该怎么做？

这时只要把两个合并到一起，就相当于删去一些边，得到最大生成树了。

我们改删边为加边，用 $\mathtt{k}\mathtt{r}\mathtt{u}\mathtt{s}\mathtt{k}\mathtt{a}\mathtt{l}$ 求最大生成树就完了。

现在我们不知道该怎么配对，怎么办呢。

先把两个根连起来是必要的，这样可以简化问题。

然后……暴力枚举是 $O(n!)$ 的，从暴力方向无法优化，因为配对后进行的最大生成树算法很复杂，是拟阵的最大权独立集。所以，基本上得确定了配对后，才可以得到算法结果的一些信息。

贪心配对？我们无法找到任何一种特征值，使得能够指导我们进行最优的配对。而且这个贪心跟最大生成树的贪心体系不同，毫无道理。

那么……看来我们是不能提前决定怎么配对的了。悲！

但是，我们求的并不是怎么配对啊！我们计算的是最大生成树。换句话说，我们求的是：对于任意的配对策略，求出的最大的生成树的值。可以换个角度：求的是最大的一个生成树的值，满足此时配对有解。

这绝对是非常合理的想法！因为对于最终的情况，去掉边的配对之后，留下来的边数量固定，说不定满足拟阵性质呢！

那么，我们可以暂时不配对（不连叶子之间的无穷大的边），直接开始跑最大生成树。

这时，由于我们的独立集定义不再是无环（生成树唯一需要满足的性质），而是还要加上最终有解性。

假设两棵树各有 $m$ 个叶子，我们判定有解当且仅当剩下的含叶子节点的连通块个数大于等于 m+1。

• 证明：先证必要性，如果连通块个数小于等于 $m$ ，接下来只能连最多 $m-1$ 条边，但是配对叶子得连 $m$ 条边，故必须大于等于 $m+1$ 个。
  再证充分性，由于连通块含叶子节点，而总共的叶子节点有 $2m$ 个，根据鸽笼原理，总有连通块的叶子节点个数 $\le 1$ ，也就是等于 $1$ 。此时有一半的 $T_1$ 叶子，有一半的 $T_2$ 叶子。
  如果刚好 $2m$ 个连通块，一定可以一一配对连边，这个不消说。否则，可以找一个叶子个数大于 1 的连通块连向另一个有可配对单个叶子节点的连通块。用反证法不难发现，只要有叶子个数大于 1 的连通块，就可以找到这样的连边。这样配对后，还有叶子节点插头的连通块会减少 1，叶子节点插头会减少 2，相当于令 $m^{\prime }=m-1$ ，分别存在 $m^{\prime }$ 个 $T_1$ 叶子插头和 $T_2$ 叶子插头时，含叶子节点的连通块个数大于等于 m’+1，还可以继续连边，直到最终把 $m$ 条边连完，可知有解。证毕。

那么我们就可以在合并并查集时判断并维护一下，做一个类 $\mathtt{k}\mathtt{r}\mathtt{u}\mathtt{s}\mathtt{k}\mathtt{a}\mathtt{l}$ 。

然后我们再证它满足拟阵性质：

• 遗传性：对于一个边集，无环且含叶连通块个数 $\ge m+1$，去掉其中的一些边，仍然无环，且含叶连通块个数只会增多。
• 交换性：对于两个边集 $A,B$ ，$|A|<|B|$ 。如果此时 $A$ 含叶连通块个数已经为 $m+1$ 了，那么导致 $|A|<|B|$ 的原因必然是：无叶连通块个数比 $B$ 多，那么由反证法可知，一定存在跨越某一无叶连通块和另一个连通块的边 $x$ 在 $B$ 中，此时 A ∪ { x } A\cup\{x\} A∪{x} 中含叶连通块个数还是 $m+1$ 个，而且无环。如果 $A$ 的含叶连通块个数大于 $m+1$ 的话，那么沿用图拟阵的性质，此时一定存在一条边 $x\in B$，满足 A ∪ { x } A\cup\{x\} A∪{x} 无环，而且加了一条边后，含叶连通块个数最多减一，仍满足要求。

于是这就是正解了，时间复杂度 $O(n\log n)$ 。

CODE

#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 200005
#define ENDL putchar('\n')
#define LL long long
#define DB double
#define lowbit(x) ((-x) & (x))
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return f * x;
}
void putuint(LL x) {
	if(!x) return ;
	putuint(x/10);putchar(x%10+'0');
	return ;
}
void putint(LL x) {
	if(!x) putchar('0');
	if(x < 0) putchar('-'),x = -x;
	putuint(x); return ;
}
const int MOD = 998244353;
int n,m,i,j,s,o,k;
struct it{
	int v;LL w;it(){v=w=0;}
	it(int V,LL W){v=V;w=W;}
};
vector<it> g[MAXN<<1];
struct ed{
	int u,v; LL w;ed(){u=v=w=0;}
	ed(int U,int V,LL W){u=U;v=V;w=W;}
}e[MAXN<<2];
bool cmp(ed a,ed b) {
	if(a.w < 0) a.w = (LL)1e18;
	if(b.w < 0) b.w = (LL)1e18;
	return a.w > b.w;
}
int cnt,ctl,cntl;
LL SUM = 0;
int fa[MAXN<<1];
bool lv[MAXN<<1];
void dfs1(int x,int ff) {
	int cn = 0;
	for(int i = 0;i < (int)g[x].size();i ++) {
		int y = g[x][i].v;
		if(y != ff) {
			dfs1(y,x);
			cn ++;
		}
	}
	if(!cn) {
		lv[x] = 1;
		if(x <= n) ctl ++;
		cntl ++;
	}
	return ;
}
int findf(int x) {return x==fa[x] ? x:(fa[x] = findf(fa[x]));}
bool unionSet(int a,int b) {
	int u = findf(a),v = findf(b);
	if(lv[u] && lv[v]) {
		if(cntl-1 > ctl) {
			fa[u] = v;
			cntl --;
		}
		else return 0;
	}
	else {
		fa[u] = v;
		lv[v] |= lv[u];
	}
	return 1;
}
int main() {
	n = read();
	for(int i = 1;i <= n*2;i ++) fa[i] = i;
	unionSet(1,n+1);
	for(int i = 1;i < n;i ++) {
		s = read();o = read();k = read();
		g[s].push_back(it(o,(LL)k));
		g[o].push_back(it(s,(LL)k));
		e[++ cnt] = ed(s,o,k);
		SUM += k;
	}
	for(int i = 1;i < n;i ++) {
		s = read()+n;o = read()+n;k = read();
		g[s].push_back(it(o,(LL)k));
		g[o].push_back(it(s,(LL)k));
		e[++ cnt] = ed(s,o,k);
		SUM += k;
	}
	dfs1(1,0);
	dfs1(n+1,0);
	sort(e + 1,e + 1 + cnt,cmp);
	for(int i = 1;i <= cnt;i ++) {
		s = e[i].u,o = e[i].v;
		LL ww = e[i].w;
		if(findf(s) != findf(o)) {
			bool rs = unionSet(s,o);
			if(rs) SUM -= ww;
		}
	}
	printf("%lld\n",SUM);
	return 0;
}