【模拟赛】图论题（Dijkstra，李超树）

最新推荐文章于 2024-03-22 22:30:26 发布

DD(XYX)

最新推荐文章于 2024-03-22 22:30:26 发布

阅读量117

点赞数

分类专栏：图论线段树文章标签：图论

本文链接：https://blog.csdn.net/weixin_43960414/article/details/122544896

版权

线段树同时被 2 个专栏收录

53 篇文章 0 订阅

订阅专栏

图论

48 篇文章 0 订阅

订阅专栏

题面

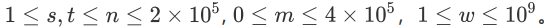
在这里插入图片描述

题解

首先，老套路，先做两遍 $\tt Dijkstra$ ，一遍从 $S$ 开始走正图，另一遍从 $T$ 开始走反图。

然后我们把从 $S$ 走到 $i$ 点的最短路记作 $L_i$ ，从 $i$ 走到 $T$ 的最短路记作 $R_i$ ，新建 $(a, b)$ 边的答案就是
$L_a+R_b+(a-b)^2\\ =L_a+R_b+a^2+b^2-2ab\\ =L_a+a^2+(-2b\cdot a+R_b+b^2)$

第三行括号里是一个关于 $a$ 的一次函数，因此我们可以把每个点作为 $b$ 产生的一次函数放到李超树上构建一个凸包，然后枚举 $a$ ，在凸包上的对应位置取得最小值。

时间复杂度 $O((n+m)\log n)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<stack>
#include<random>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 400005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
//#define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

int n,m,s,o,k;
int hd[MAXN],nx[MAXN<<1],v[MAXN<<1],w[MAXN<<1],cne;
int hd2[MAXN];
void ins(int x,int y,int z) {
	nx[++cne] = hd[x]; v[cne] = y; w[cne] = z; hd[x] = cne;
	nx[++cne] = hd2[y]; v[cne] = x; w[cne] = z; hd2[y] = cne;
}
LL dp1[MAXN],dp2[MAXN];
LL *dp;
int tr[MAXN<<1];
int mg(int a,int b) {
	if(!a || !b) return a+b;
	return dp[a] < dp[b] ? a:b;
}
void upd(int x,int y) {
	tr[n+x] = y;
	for(int s=(n+x)>>1;s;s>>=1) {
		tr[s] = mg(tr[s<<1],tr[s<<1|1]);
	}return ;
}
void dij(int S,int *hd,LL *DP) {
	dp = DP;
	memset(tr,0,sizeof(tr));
	for(int i = 0;i <= n;i ++) dp[i] = 1e18;
	dp[S] = 0; upd(S,S);
	for(int i = 1;i < n;i ++) {
		int t = tr[1];
		if(!t) break;
		for(int j = hd[t];j;j = nx[j]) {
			if(dp[t] + w[j] < dp[v[j]]) {
				dp[v[j]] = dp[t] + w[j];
				upd(v[j],v[j]);
			}
		}
		upd(t,0);
	}return ;
}
struct it{
	LL a,b;
	it(){a=0;b=1e18;}
	it(LL A,LL B){a=A;b=B;}
	LL F(int x) {return a*x+b;}
}tre[MAXN<<2];
void addtree(int a,int al,int ar,it y) {
	LL l1 = tre[a].F(al),r1 = tre[a].F(ar);
	LL l2 = y.F(al),r2 = y.F(ar);
	if(l1 <= l2 && r1 <= r2) return ;
	if(l2 <= l1 && r2 <= r1) {tre[a] = y;return ;}
	int md = (al + ar) >> 1;
	addtree(a<<1,al,md,y); addtree(a<<1|1,md+1,ar,y);
	return ;
}
LL findmin(int a,int x,int al,int ar) {
	if(al > x || ar < x) return 1e18;
	if(al == ar) return tre[a].F(x);
	int md = (al + ar) >> 1;
	return min(tre[a].F(x),min(findmin(a<<1,x,al,md),findmin(a<<1|1,x,md+1,ar)));
}
int main() {
	freopen("graph.in","r",stdin);
	freopen("graph.out","w",stdout);
	n = read();m = read();
	int S = read(),T = read();
	for(int i = 1;i <= m;i ++) {
		s = read();o = read();k = read();
		ins(s,o,k);
	}
	dij(S,hd,dp1); dij(T,hd2,dp2);
	LL ans = dp1[T];
	for(int i = 1;i <= n;i ++) {
		addtree(1,1,n,it(-2ll*i,i*1ll*i + dp2[i]));
	}
	for(int i = 1;i <= n;i ++) {
		ans = min(ans,i*1ll*i + dp1[i] + findmin(1,i,1,n));
	}
	AIput(ans,'\n');
	return 0;
}