【模拟赛】立体几何（图论，三元环计数，四元环计数）

最新推荐文章于 2024-09-15 22:57:23 发布

原创最新推荐文章于 2024-09-15 22:57:23 发布 · 640 阅读

2 ·

CC 4.0 BY-SA版权

数学同时被 3 个专栏收录

118 篇文章

订阅专栏

图论

48 篇文章

订阅专栏

搜索

14 篇文章

订阅专栏

本文详细探讨了一种求解最坏情况下的四点共面数的算法，涉及三维空间中线段平行、三点共线、中位线等概念。通过分类讨论，提出四种情况并给出解决方案，包括边中点、结点共面的计数方法。最终，通过数学计算和编程实现，得出解答问题的高效算法，总时间复杂度为O(mm)。

题面

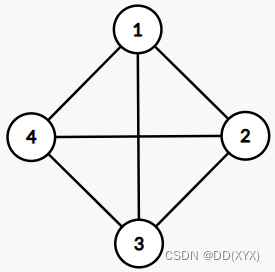
在这里插入图片描述

样例

样例图

在这里插入图片描述

题解

看到这个提示，我们应该大概能猜到用意了。

我们求的其实是最坏情况下的四点共面数，~~这个期望根本就™没用~~。

四点共面数好像挺复杂，我们分情况讨论吧：

我首先想到，如果两线段在三维空间中平行，那么四个端点一定共面。而中点恰好带来了平行的好条件：中位线。所以第一种情况：四元环的四条边中点——连成两个线段，分别与同一条对角线平行，所以两线段平行，四点共面；在样例中，可惜只有 3 种情况，目前离 69 还差得远。
然后我想到，如果存在三点共线，那么随便找一个第四点就能共面了，而三点共线只可能是一整条边。第二种情况：一条边中点&两端点 + 任意一点。这个情况就比较多了，我们只需要随便选 $m$ 条边之一，再从 $(n + m - 3)$ 个点中选一个第四点， $m⋅(n+m−3)m\cdot(n+m-3)$ 。样例中有 42 种情况。
上一条其实统计了所有“间”的情况（结点+中点+结点），通过有机化学的思路，我们其实早该想想“邻”的情况。这时，我们要保证不与“间”的情况重复，就只能是 “结点+结点+中点+中点” 。此时我们联想到 共用端点的两线段一定是共面的 ，于是，这种类别就对应了一个角。样例中每个点连了三条边，故总计 $4⋅C32=124\cdot C_{3}^2=12$ 种。
四个中点，一个中点，两个中点的情况都讨论了，我们来讨论三个中点的情况。三中点+一结点，只能是在三角形内了。第四种情况：三元环三边中点+三结点之一。样例中共有 12 种。

四个结点是不可能的。

总计 69，和样例一致了，不管了😡。

令三元环个数为 $c_3$ ，四元环个数为 $c_4$ ，答案就是
$c3\cdot 3+c4+m\cdot (n+m-3)+\sum_{x\in V}C_{deg(x)}^2$

求三元环个数，我们可以把边重定向，度数小的点连向度数大的点，这样每个点的出度就不超过 $m\sqrt m$ 。利用这个性质，我们在每个三元环的度数最少结点处统计贡献，先标记一次所有出点，再统计暴力走两步到达标记点的方案数。总时间复杂度 $O(mm)O(m\sqrt m)$ 。

求四元环个数，我们可以用类似的思路。我们在每个四元环度数最大结点的对点处统计贡献。对于起点 $x$ 枚举走两步到达的点，只不过第一步走原图无向边，第二步走定向图有向边。排除掉度数排名小于等于 $x$ 的点，设点 $i$ 被走到的次数为 $w_i$ ，那么将产生 $C_{w_i}^2$ 的贡献。总时间复杂度 $O(mm)O(m\sqrt m)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 500005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
//#define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

const int MOD = 998244353;
int n,m,s,o,k;
int U[MAXN],V[MAXN];
int hd[MAXN],nx[MAXN<<1],v[MAXN<<1],cne,ind[MAXN];
void ins(int x,int y) {
	nx[++ cne] = hd[x];v[cne] = y;hd[x] = cne;ind[y] ++;
}
vector<int> g[MAXN];
int f[MAXN];
bool cmp(int a,int b) {
	if(ind[a] != ind[b]) return ind[a] < ind[b];
	return a<b;
}
int main() {
    freopen("graph.in","r",stdin);
    freopen("graph.out","w",stdout);
    int T = read();
	while(T --) {
		n = read();m = read();
		cne = 0;
		for(int i = 1;i <= n;i ++) hd[i] = 0,ind[i] = 0,g[i].clear();
		for(int i = 1;i <= m;i ++) {
			U[i] = s = read();V[i] = o = read();
			ins(s,o); ins(o,s);
		}
		for(int i = 1;i <= m;i ++) {
			if(U[i] > V[i]) swap(U[i],V[i]);
			if(ind[U[i]] > ind[V[i]]) swap(U[i],V[i]);
			g[U[i]].push_back(V[i]);
		}
		LL c3 = 0,c4 = 0;
		for(int i = 1;i <= n;i ++) {
			for(int y:g[i]) f[y] = 1;
			for(int y:g[i]) {
				for(int z:g[y]) if(f[z]) c3 ++;
			}
			for(int y:g[i]) f[y] = 0;

			for(int j = hd[i];j;j = nx[j]) {
				for(auto y:g[v[j]]) {
					if(cmp(i,y)) c4 += f[y],f[y] ++;
				}
			}
			for(int j = hd[i];j;j = nx[j]) {
				for(auto y:g[v[j]]) {
					f[y] = 0;
				}
			}
		}
		LL ans = m*1ll*(n+m-3)%MOD;
		for(int i = 1;i <= n;i ++) {
			(ans += ind[i] *1ll* (ind[i] - 1)/2 % MOD) %= MOD;
		}
		ans = (c3*3ll + c4 + ans) % MOD;
		AIput(ans,'\n');
	}
	return 0;
}