LEU信号的图像预处理 （一）混合波形的分离与提取

本人是刚步入工作的菜鸟，文章中如果有专业术语表述不当或错误的地方希望大家批评指正。
本文讨论的是最近在做的铁路信号系统的LEU测试装置项目的一些图像问题。
LEU会向应答器发送一系列波形，以波形的形状来传递信号（01信号），本文的目的是通过对LEU发出的波形数据的计算，检验LEU的各项参数是否符合需求。
已将待测LEU信号的一部分用示波器导出的数据存放在网盘中，里面是按不同精度导出的数据(此数据的合格性、标准性有待检测)。链接：[https://pan.baidu.com/s/10ka7e96zhmMMFZW0860DmQ]
提取码：dus5
首先，直接使用Matlab绘图，所得出的图像与放大后的部分图像如图（它的X轴为时间，单位为s，Y轴为电压，单位为V，图像由多个离散的点连接所描出）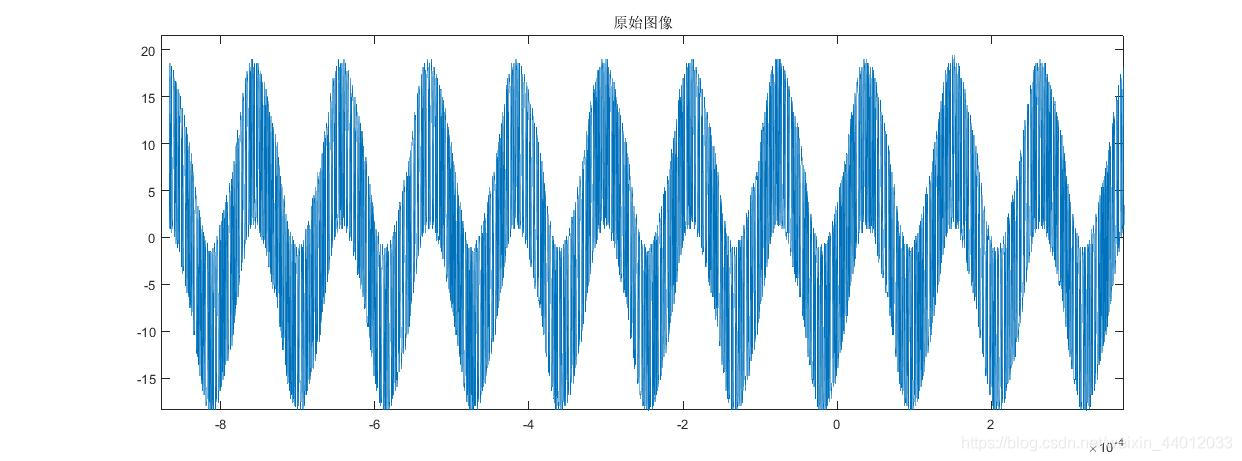


它是一个较小周期的波（称它为C1信号）与一个较大周期的波（称它为C6信号）的混合波。
目标任务如下：
1.连接170Ω阻性负载时，计算每个C6波形的峰值，验证其是否符合大于20V，小于23V的要求。
2.C6信号为正弦波，频率为8.82kHz±0.1kHz。
3、计算连接120Ω阻性负载时，C1的实际信号幅度，验证其是否满足每个信号的幅度在14V-18V之间
4.计算连接120Ω阻性负载时，每个C1信号的上升沿和下降沿（10%-90%）的时间，验证是否每个C1波形的该时间都大于100ns。
5.计算各不同阻性负载下的平均数据速率，方法为：计算LEU传递1500位数据所花的时间，进而求得这1500位上的平均数据速率。
6.计算连接120Ω阻性负载时，每个C1信号的周期与幅值，验证每个C1信号是否会进入阴影区域或将所有信号叠加，验证其是否能将标准眼图放在里面。
本文首先讨论此混合波形的分离与提取的几种方法，其他的问题的解决思路与方法，将逐渐在后面的文章中提供。

想要分析与计算这两种波形的信息与各项参数，首先要做到的就是分离这两种信号。
方法一：通过上下轮廓对C6信号进行提取
由于混合波形的上下轮廓（不考虑C1具体波形的情况下）可作为C6信号提取的依据，所以本文通过混合波形的上下轮廓来计算处于图像中央的C6的正弦波形。
区间覆盖法来“描”出它的轮廓：可以发现，混合波的上轮廓一直处于大于零的状态，建立多个在X轴，即时间轴上的小区间，每个小区间的宽控制在一个C1波的周期到两个C1波的周期之间（可以通过在图像上描点得到一个大概的值，此参数不要求高精度），每一个这样的区间实质上为时间轴上的两点，以此两点画平行于Y轴的直线，建立一个矩形，使得这个矩形刚好能把所在X区间的混合波“框住”，在此X区间里提取混合波数据点的在Y上的最大值最小值，建立每个区间独有的矩形，该矩形的两个相对的顶点为刚刚找出的最大值与最小值点，可以参考下图中红色圆圈标注的点。在实际计算中，将所有数据点按Y坐标的正负分成两部分。在X轴上方的部分按区间找出最大值然后连接，在X轴下方的部分按区间找出最小值然后连接。这样，就描出了C6的轮廓。调整区间的宽度使得寻找最大最小值点时不会进入C1的波形中，保证所提取的点皆为C1波形的一周期内的最大或最小值。
而在同一区间找出的最大值点与最小值点中间的点，可以近似认为是C6波形上的数据点（在下面会分别尝试将上轮廓、下轮廓或中间点作为C6波形上的点来做拟合）

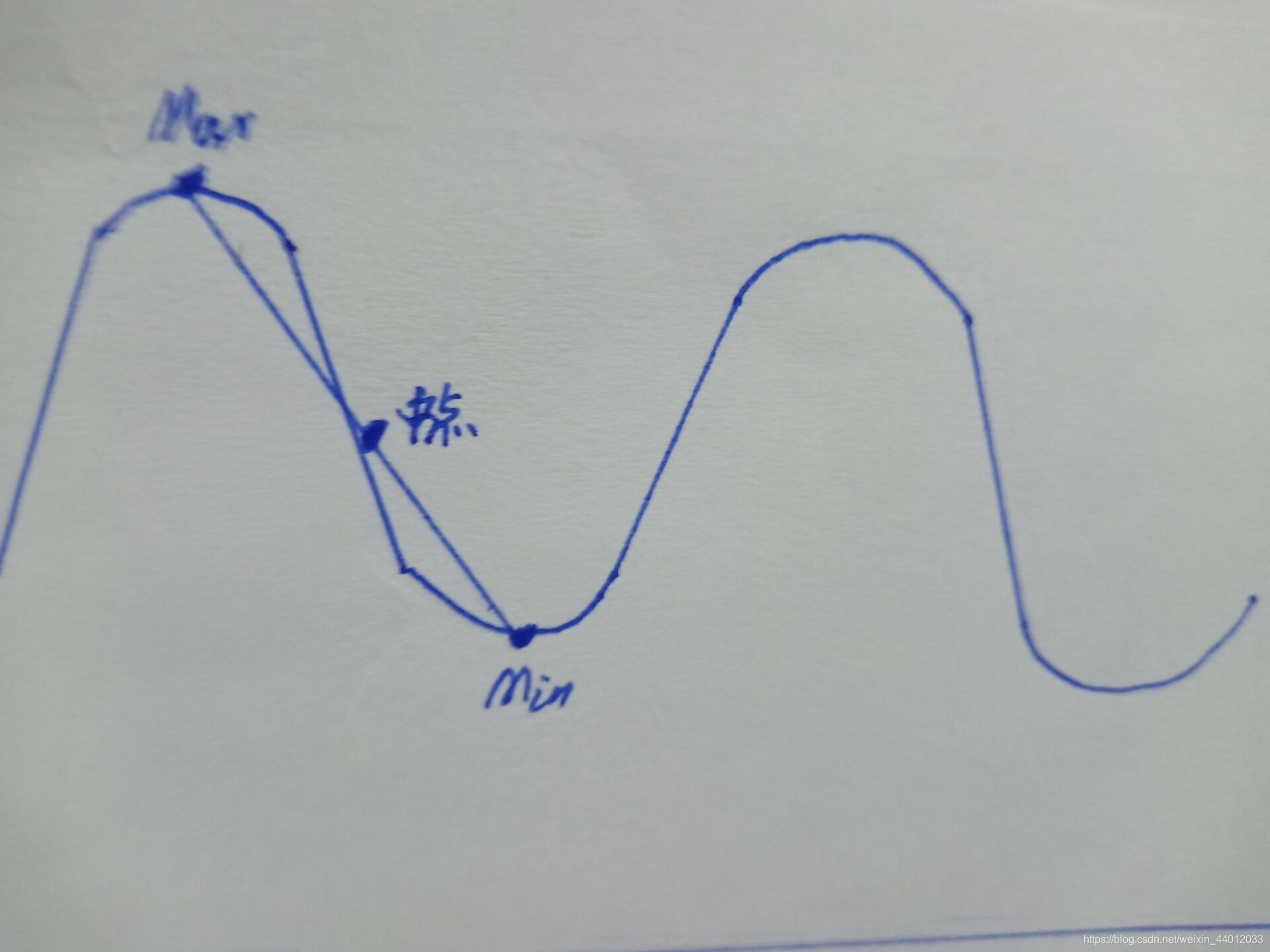
这样的话，用合适大小的区间覆盖整个信号，并将提取出的数据点进行绘图检验，如果最大最小值没能出现在每个C1波的上下顶点，则适当调大时间区间长度。得到混合波形的轮廓与C6实际波形的一部分坐标点，示意如下：

假设C6波为一个标准的正弦波，不妨设它的方程为：

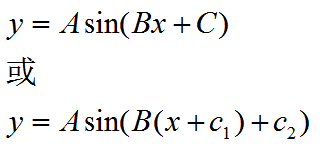
在正弦方程中，A代表波形的幅值，B代表波形的频率，C代表波形的相位。上文中已经计算上下轮廓点与中间值点，不妨分别计算所有上轮廓点的最大值和最小值，取两者之差，同理计算所有下轮廓的这两者之差。这两个差的平均值的二分之一作为A的近似值。
接下来计算公式中C的值，C实际上为x轴(时间轴的平移大小),首先，使用上述通过C6波形轮廓计算出的实际波形的部分坐标点，从实际数据点饿第一个点开始，寻找大约两个C1周期内的，纵坐标最高的坐标点，该坐标点对应正弦曲线在x=π/2时的坐标点。设该坐标点的x坐标为c1，则C6波形可写为：
至此，C6波形仅剩一个参数B未确定，以下描述B的计算方法
（1）设上述由上下轮廓计算得到的一组C6波形上的点（离散点）为：

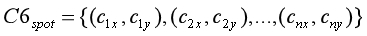
（2）设定一组向量，(在B的可能范围内均匀取点）如果CB的覆盖范围足够大，且覆盖精度较高，则可通过将CB中的每个元素替代方程中的B值，并计算将各个值带入后的波形与实际计算出的中心点的误差，然后取误差最小的作为实际B值
（3）由于C6的标准正弦近似方程为：

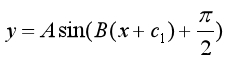
将向量CB中的每个值代入方程的B值，x为
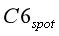各点的x坐标，即Cix，由此计算得到对应的y值CBiy
对于CB中每个值，计算对应误差，公式为：

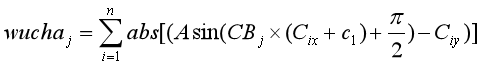
计算完成后，找出该向量的最小值，与其对应的CB中的近似B值则为寻找出的最优B值。拟合结果如下

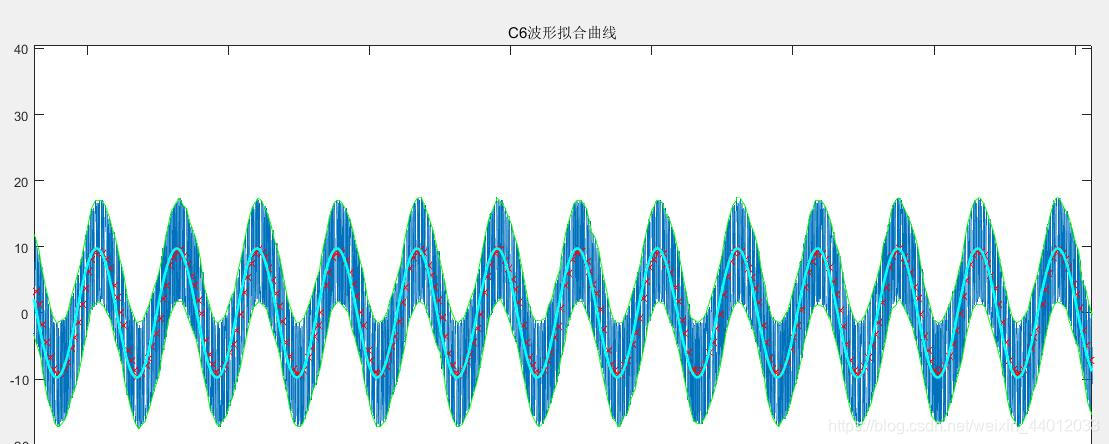
混合波形减去C6后的图形如下：

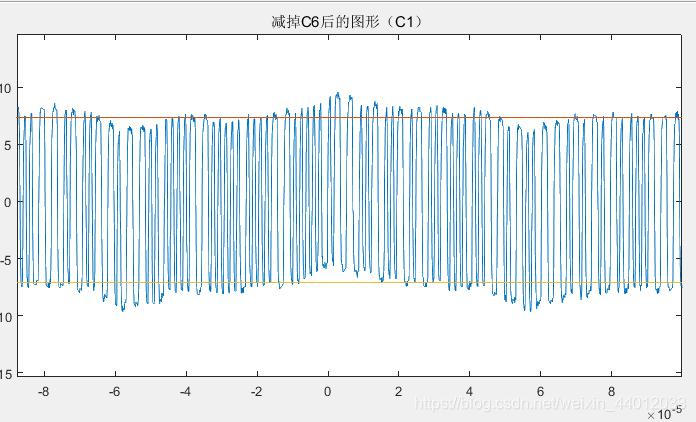
误差估计：通过此方法寻找出的B值的误差范围取决于拟合的精度，在计算中，B的误差小于0.1。由于此B值需要的计算量不大，所以仅设计了一般的遍历算法。
方法评估：使用上下轮廓法来计算，主要误差由轮廓点与上下轮廓中间点造成，B的计算结果与示波器显示的数据，误差在1%-2%。但对于一组中含有多个周期的数据，误差累计之后非常严重，下面尝试先计算周期，以周期算频率的方法，计算C6的波形方程。
**方法二：**以近似周期来计算C6的波形方程
大概方法可以如下图所示
首先，需要找出混合波形每个较大周期波形的最高点，如果可以找到每个峰值点，那每两个峰值点之间的时间上的差即为半周期，计算平均值之后，再由周期计算频率。
下面讨论寻找此类点的方法：
虽然对于混合波的每个“周期”来说，它的半周期上的最大值为想要求的峰值点，最小值为最低峰值点，但是对于多周期混合波来说，很难估计周期的值，如果使用"区间覆盖法"，区间的值误差较大，会和方法一一样掉入误区中。
在整个混合波型数据中，找出在Y轴上坐标最大的点，做一条过该点平行于X轴的直线，该直线的X坐标可限制在这组数据在X轴上的最小值到最大值的范围。这条直线可近似认为是上图七中的自上而下第三条直线。为什么要画出这条直线呢？是因为这样可以通过设定参数将混合波形最上面的一部分截取出来，比如我将参数设置为0.8，意义在于将刚刚画出的直线的纵坐标缩小至它的0.8倍，通过算法截取在这条直线上面的点，就会得到：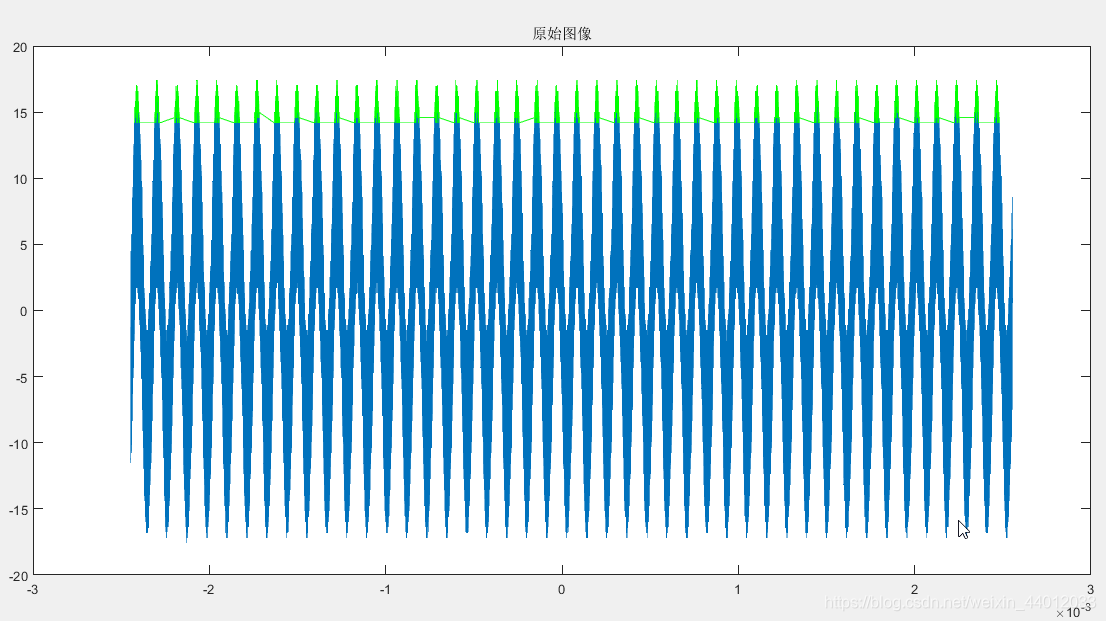
这样，就将在混合波性上求各峰值点的问题转化为求绿色部分点的各“组”点的最大值，这样它的特征更加明显，也更加容易计算。
之后，第一步就是将所有绿色点进行分离，使得每组点含且只含有一个峰值点。可以进行分离的原因是这组点有特征存在。由图可知，一组点和相邻的一组点，在边界上的点的距离远高于同一组点的距离，所以可以设置一个距离参数，如果这个参数小于相邻两组点之间的距离而大于同一组点中相邻两个点之间的距离。（此处的距离指两个数据点在X坐标上的差）
遍历求绿色部分点中后一个点与前一个点在X坐标上的差，当这组点后一个点与前一个点在X坐标上的差大于所设参数时，就意味着此时计算的两个点，分别属于不同峰值点的范围。

基于此，就可以将每个峰值点所在的范围划分出来，然后就很简单了，在每一个这样的范围内，寻找最大值点，找出所有这样的最大值点后，忽略第一个与最后一个点，求中间点中相邻两个点的X上的距离的平均值，就近似认为这个平均值为C6正弦波的半周期，由此求得C6波形方程的B值。如果想要计算结果更精确，可以使用同样的方法计算下峰值的相邻两点差的平均值，再与上述结果求平均。对于C6波形方程

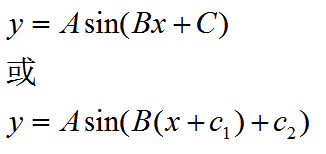
中的参数A的计算，暂时只有方法一中的所介绍的方法，精度由所定参数来决定，由于C1波形的不规范性，需要多次绘图检验划定区间。
需要注意的是，此方法中C的值需要改进，在使用方法二时发现，B的值精确程度明显提高，但C的值对最终结果产生了较大影响。所以使用遍历的方法求C的近似值：
由于C6的正弦方程中A,B的值已确定，所以可以通过方程来寻找C的近似值。其原理与方法一中求B值时相同，在此不做赘述。具体过程可查看算法。
如果参数B的误差可以接受，那么A与C的误差在一定范围内对C6的波形的影响还是可以接受的。对其中的一组数据，提取结果如下：


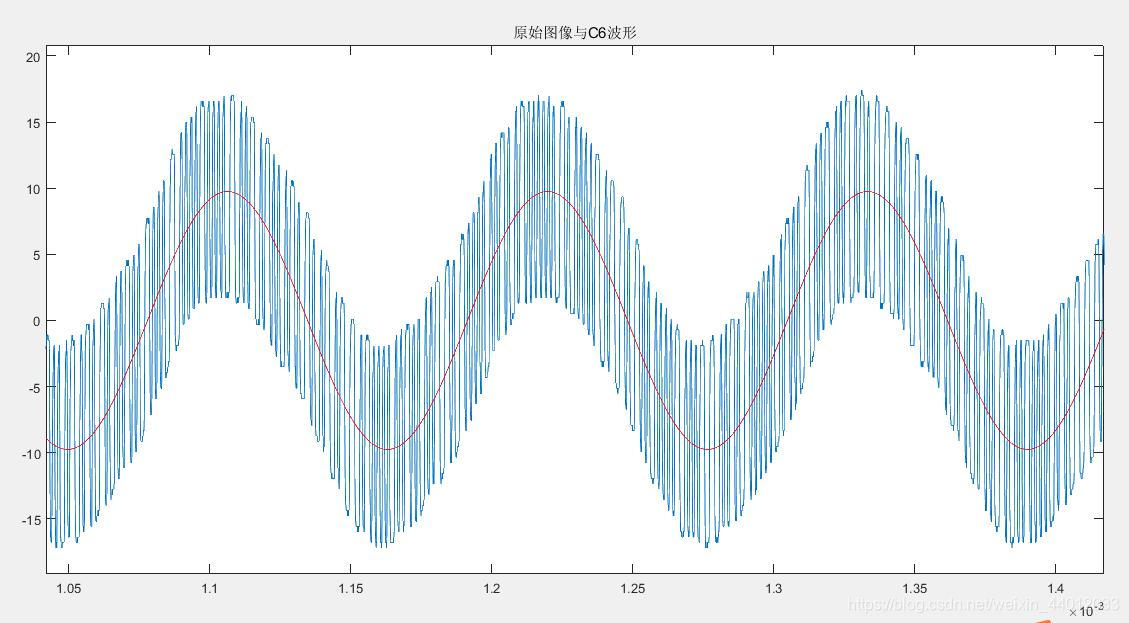
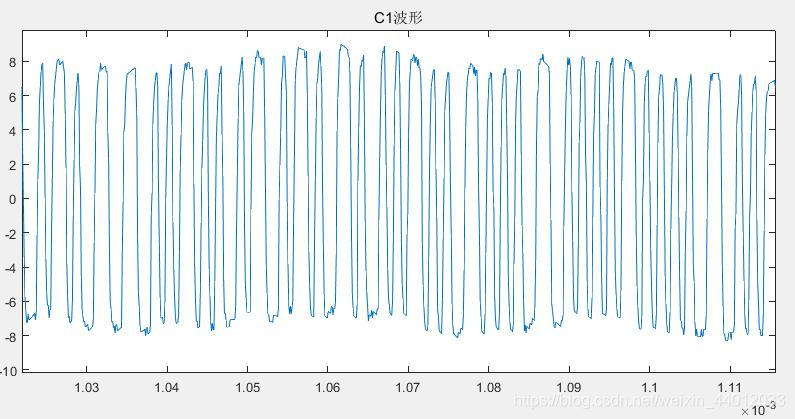
由上述两个方法可知，方法二对波形的提取更为准确。
下面为方法一与方法二的MATLAB代码实现：
方法一
*
脚本函数
data=xlsread(‘C:\Users\Administrator\Desktop\工作\信号文件\可使用\scope_31_NO_LBL.xls’);
x1=data(1:end,1);
y1=data(1:end,2);
BL_A=0.95;%参数一%A的缩减比例
kuadu=0.000005;
Yzhou=0.0002;
kuaduC1=0.000015;%计算C1上下轮廓（峰值）时所用到的小矩形在X轴上的宽
C1BO_zhouqi=0.0000011.2;
%%%%%%%%%%%%
[A,XYjunzhi,XYup,XYdown] =fc6_A(x1,y1,kuadu);%求A并返回上下轮廓和中心描点数据，方便进行绘图数据
[Mx,My] =fc6_C(x1,y1,Yzhou); %计算C时，求数据初始点附近大约一个周期内的（大小为30.-4）范围内的最大值，并求得该点坐标
[B,shijix,shijiy]=fc6_B(XYjunzhi,Mx,A,x1);%设置计算误差的函数，调整计算B，造成的偏差，并记录,找出最小偏差，以逼近C6
C=Mx(1);
disp(['C6峰值 ',num2str(A)])
pinlv=1/(2pi/B)0.001;
disp([‘C6频率为’,num2str(pinlv),‘KHz’])
disp(‘C6波形拟合方程为’)
disp([‘y=’,num2str(A),‘sin(’,num2str(B),’(x-’,num2str©,’+pi/2)’]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1)%绘图一：原始图像
plot(x1,y1)
hold on
sefx=x1;
sefy=Asin(B*(x1-C)+pi/2);
plot(sefx,sefy,‘r’)
title(‘原始图像与C6波形’)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2)
plot(x1,y1)%绘图一：原始图像
hold on
plot( XYup(:,1), XYup(:,2),‘g-’,XYdown(:,1), XYdown(:,2),‘g-’)%绘图二：大波形（C6）的轮廓
hold on
plot( XYjunzhi(:,1), XYjunzhi(:,2),‘rx’)%绘图二：大波形（C6）的中间点
title(‘描出轮廓与中间点’)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3)
spotsum=5000;
Xsefx=x1;
Ysefy=y1-Asin(B(x1-C)+pi/2);
plot(Xsefx,Ysefy)
title(‘C1波形’)

调用函数
function [A,XYjunzhi,XYup,XYdown] =fc6_A(x1,y1,kuadu)
%求A并返回上下轮廓和中心描点数据，方便进行绘图数据
XSTART=min(x1);
XEND=max(x1);
[LX,MX]=size(x1);
%裁剪，每个X的跨度为0.000005
qujian=XSTART:kuadu:XEND;
[Lq,Mq]=size(qujian);
XYup=zeros(1,2);%存储目标点的坐标(上)
XYdown=zeros(1,2);%存储目标点的坐标(下)
XYjunzhi=zeros(1,2);%存储目标点的坐标(下)
for xq=2:Mq-1
Y=zeros(1,2);%存储当前X区域内的点的纵坐标
for t=1:LX
if x1(t)>=qujian(xq-1)&&x1(t)<qujian(xq)
Y=[Y;x1(t),y1(t)];
end
end
Y=Y(2:end,:);
[Ymax,wup]=max(Y(:,2));
[Ymin,wdown]=min(Y(:,2));
XYup=[XYup;Y(wup,:)];
XYdown=[XYdown;Y(wdown,:)];
%Y(wup,:)%上面的一个数据点
%Y(wdown,:)%下面的一个数据点
junzhix=(Y(wup,1)+Y(wdown,1))/2;
junzhiy=(Y(wup,2)+Y(wdown,2))/2;
XYjunzhi=[XYjunzhi;junzhix,junzhiy];
end
XYup=XYup(2:end,:);
XYdown=XYdown(2:end,:);
XXYup=XYup(:,2);
XXYdown=XYdown(:,2);
%%%%%%%%%%%%%%%%%%%%
%设C6波为y=Asin(Bx+C)或y=Acos(Bx+C)，则
XYjunzhi=XYjunzhi(2:end,:);
A=(abs(max(XYdown(:,2))-min(XYdown(:,2)))+abs(max(XYup(:,2))-min(XYup(:,2))))/4;
end

function [B,shijix,shijiy]=fc6_B(XYjunzhi,Mx,A,x1)
% 注意BX为参数，对于周期变化较大的波，应注意调整该参数
[LMy,MMy]=size(XYjunzhi);
Sumresult=[];
format shortG
for bx=30000:1:60000%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%调控参数
Sum=0;
shijiy1=0;
for ii=1:LMy
shijiy1=Asin(bx(XYjunzhi(ii,1)-Mx(1))+pi/2);
Sum=Sum+abs(XYjunzhi(ii,2)-shijiy1);
end
Sumresult=[Sumresult;Sum;];
end
[Smin,Lmin]=min(Sumresult);
B=30000+(Lmin-1);%最优B值
%以下为绘图准备数据
shijix=x1(:,1);
shijiy=Asin(B(shijix-Mx(1))+pi/2);
end

function [Mx,My] =fc6_C(x1,y1,Yzhou)
%求C----Mx(1)
CY=[];
[LX,MX]=size(x1);
XSTART=min(x1);
for C=1:LX
if x1©<=XSTART+Yzhou
CY=[CY;x1©,y1©];
end
end
[CYmax,ww]=max(CY(:,2));
Mx=x1(ww:end);%用于计算拟合曲线的C
My=y1(ww:end);%用于拟合曲线描点的纵坐标，注意，已裁剪了一部分
end

方法二：
脚本函数
data=xlsread(‘C:\Users\Administrator\Desktop\工作\信号文件\可使用\scope_31_NO_LBL.xls’);
x1=data(1:end,1);
y1=data(1:end,2);
%%%%%%%%%%%%
BL_A=1.1;%参数一%A的缩减比例
kuadu=0.000005;%小矩形的宽（X坐标轴上的跨距），用于包裹并计算大图像的轮廓
Yzhou=0.0003;%参数三用于计算C6的拟合波形中的参数C
%%%%%%%%%%%%
[A,XYjunzhi,XYup,XYdown] =fc6_A(x1,y1,kuadu);%求A并返回上下轮廓和中心描点数据，方便进行绘图数据
B=fc6_B2(x1,y1);
C=fc6_C2(XYjunzhi,A,B);
%%%%%%%%%%%%到此，将C6信号，计算完毕
%%%%%%%%%%%%%%%%%%%%%%%%
disp(['C6峰值 ',num2str(A)])
pinlv=1/(2pi/B)0.001;
disp([‘C6频率为’,num2str(pinlv),‘KHz’])
disp(‘C6波形拟合方程为’)
disp([‘y=’,num2str(A),‘sin(’,num2str(B),’(x-’,num2str©,’+pi/2)’]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1)%绘图一：原始图像
plot(x1,y1)
hold on
sefx=x1;
sefy=Asin(B(x1-C)+pi/2);
plot(sefx,sefy,‘r’)
title(‘原始图像与C6波形’)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(2)
plot(x1,y1)%绘图一：原始图像
hold on
plot( XYup(:,1), XYup(:,2),‘g-’,XYdown(:,1), XYdown(:,2),‘g-’)%绘图二：大波形（C6）的轮廓
hold on
plot( XYjunzhi(:,1), XYjunzhi(:,2),‘rx’)%绘图二：大波形（C6）的中间点
title(‘描出轮廓与中间点’)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(3)
spotsum=5000;
Xsefx=x1;
Ysefy=y1-Asin(B(x1-C)+pi/2);
plot(Xsefx,Ysefy)
title(‘C1波形’)

调用函数
function [A,XYjunzhi,XYup,XYdown] =fc6_A(x1,y1,kuadu)
%求A并返回上下轮廓和中心描点数据，方便进行绘图数据
XSTART=min(x1);
XEND=max(x1);
[LX,MX]=size(x1);
%裁剪，每个X的跨度为0.000005
qujian=XSTART:kuadu:XEND;
[Lq,Mq]=size(qujian);
XYup=zeros(1,2);%存储目标点的坐标(上)
XYdown=zeros(1,2);%存储目标点的坐标(下)
XYjunzhi=zeros(1,2);%存储目标点的坐标(下)
for xq=2:Mq-1
Y=zeros(1,2);%存储当前X区域内的点的纵坐标
for t=1:LX
if x1(t)>=qujian(xq-1)&&x1(t)<qujian(xq)
Y=[Y;x1(t),y1(t)];
end
end
Y=Y(2:end,:);
[Ymax,wup]=max(Y(:,2));
[Ymin,wdown]=min(Y(:,2));
XYup=[XYup;Y(wup,:)];
XYdown=[XYdown;Y(wdown,:)];
%Y(wup,:)%上面的一个数据点
%Y(wdown,:)%下面的一个数据点
junzhix=(Y(wup,1)+Y(wdown,1))/2;
junzhiy=(Y(wup,2)+Y(wdown,2))/2;
XYjunzhi=[XYjunzhi;junzhix,junzhiy];
end
XYup=XYup(2:end,:);
XYdown=XYdown(2:end,:);
XXYup=XYup(:,2);
XXYdown=XYdown(:,2);
%%%%%%%%%%%%%%%%%%%%
%设C6波为y=Asin(Bx+C)或y=Acos(Bx+C)，则
XYjunzhi=XYjunzhi(2:end,:);
A=(abs(max(XYdown(:,2))-min(XYdown(:,2)))+abs(max(XYup(:,2))-min(XYup(:,2))))/4;
end

function B=fc6_B2(x1,y1)
%重新算一下B
C6zujv=0.00009;%用于检验两点是否属于同一组别
[LX,MX]=size(x1);
C6feng_up=max(y1)0.9;
%C6feng_down=min(y1)0.9;
Yup=[];
for t=1:LX
if y1(t)>=C6feng_up
Yup=[Yup;x1(t),y1(t)];
end
end
%检查并筛学出一组一组的点
[LYup,MYup]=size(Yup);
jieduandian=[];
for k=1:LYup-2
if Yup(k+1,1)-Yup(k,1)>C6zujv
jieduandian=[jieduandian;Yup(k,1);Yup(k+1,1);];
end
end
%舍弃第一个之后，寻找每两个点之间的最大值点
jieduandian=jieduandian(2:end);
[Lj,Mj]=size(jieduandian);
%jieduandiande1-2 3-4…范围内点的最大值
Ljieduan=floor(Lj/2);
resultJ=[];
for kt=1:Ljieduan
YX=[];%设定临时存储变量
for g=1:LYup
if Yup(g,1)<jieduandian(2kt)&&Yup(g,1)>jieduandian(2kt-1)
YX=[YX;Yup(g,:)];
end
end
if isempty(YX)==0
[mYX,LYX]=max(YX(:,2));
resultJ=[resultJ;YX(LYX,:);];
end
end
[LresultJ,MresultJ]=size(resultJ);
%计算resultJ两点之间的差
CtJ=[];
for gt=1:LresultJ-1
CtJ=[CtJ;resultJ(gt+1)-resultJ(gt)];
end
%CtJ
resultB=1/mean(CtJ)
B=2*pi/(1/resultB)
end

function C =fc6_C2(XYjunzhi,A,B)
Sumresult=[];
[LXjun,MXjun]=size(XYjunzhi);
for CcCc=0:0.0000001:0.001%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%调控参数
Sum=0;
shijiy1=0;
for ii=1:LXjun
shijiy1=Asin(B(XYjunzhi(ii,1)-CcCc)+pi/2);
Sum=Sum+abs(XYjunzhi(ii,2)-shijiy1);
end
Sumresult=[Sumresult;Sum;];
end
[Smin,Lmin]=min(Sumresult);
C=0.0000001*(Lmin-1);%最优C值
end