三支冲突分析介绍

七玄桐

已于 2024-04-09 23:18:17 修改

阅读量708

点赞数 3

文章标签：学习笔记

于 2024-04-09 23:12:19 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_44014836/article/details/137568002

版权

本文介绍了Pawlak的冲突分析模型，如何通过决策矩阵的二元关系形式表示对象对属性的态度，并详细解释了姚一豫教授的改写版本，包括支持集、反对集和中立集的划分，以及基于这些概念的二元关系和距离运算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Pawlak最早通过观察一组智能体对一组问题的意见，提出了冲突分析模型。U表示对象集，V表示属性集，R表示对象集和属性集之间的二元关系，这样一个刻画冲突分析的信息系统通过三元组（U，V，R）表示，其中，每个对象对属性的态度记为R（x，a）。实质上就是决策矩阵的二关关系形式表达。

Pawlak冲突分析模型中，R（x，a）取值为1，-1和0，分别代表支持反对和中立， $\phi_a(x,y)$ 表示对象x和y对属性a的一致性，取值范围也是1，-1和0，分别代表两者对属性a持一致态度，两者对属性a持相反态度，以及两者对属性a具有不同态度。然后定义了对象x和y之间的距离，表示x和y对所有属性计算态度一致性的算术平均，实质上就是决策矩阵中两行算距离。最后通过0.5阈值判断结果x和y是否冲突。

例子1

这张表就是Pawlak论文使用的示例，通过情况表很容易看出，针对i1这个属性，a2、a3和a5支持，a1反对，a4和a6中立。

姚一豫教授重新改写了冲突分析模型的定义，给出了三支冲突分析的定义如下。

定义在一个情况表中，对于所有的属性i，对象集可以划分为以下三个部分： $A_i^-={x\in A|r(x,i)=-1}, A_i^0={x\in A|r(x,i)=0}, A_i^+={x\in A|r(x,i)=1},$

分别代表属性的支持集，反对集和中立集。

例子2 重新分析例子1的表，那么可以得到关于属性i1的支持集，反对集和中立集 $A_{i_1}^-=\{a_1\},A_{i_1}^0=\{a_4,a_6\},A_{i_1}^+=\{a_2,a_3,a_5\}$ 。

进一步的，我们考虑属性的笛卡尔积形式。

定义基于两个对象的评价，可以定义三种二元关系来描述他们的关系：

$R_i^=={(x,y)\in A \times A|(r(x,i)-r(y,i)/2=0)}$

$R_i^\approx ={(x,y)\in A \times A|(r(x,i)-r(y,i)/2=0.5)}$

$R_i^\asymp ={(x,y)\in A \times A|(r(x,i)-r(y,i)/2=-1)}$

其中，定义了一种距离运算 $d(a,b)=0.5|a-b|$ ，||就是绝对值运算。这样我们就能很容易的算出所有的二元关系的结果如下表所示，比如]-1-(-1)|=0，以此类推。

关系 $R_i^=$ 描述了两个对象对属性的评价是一致或相等的，并且实质上是一个等价关系。关系 $R_i^\approx$ 描述了必须有且只有一个对象的评价是0，另一个对象评价是1或-1的情况，实质上是一个相容关系。关系 $R_i^\asymp$ 描述了两个对象对属性是完全不同的正负对立的评价。

上表可以转换成如下等式来描述，比如 $R_i^=$ 关系就包括了负负、00和正正三种情况，以此类推。

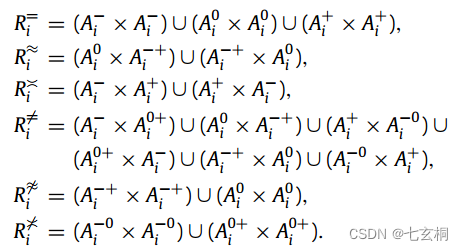
以上就是三支冲突分析的所有概念部分的介绍，具体细节请参考文献：Three-way conflict analysis: Reformulations and extensions of the Pawlak model。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。