LCA(最近公共祖先)+RMQ(区间最值)详解

最新推荐文章于 2022-11-24 09:59:51 发布

ReverieZH

最新推荐文章于 2022-11-24 09:59:51 发布

阅读量886

点赞数 3

分类专栏： ACM 文章标签： acm LCA RMQ

本文链接：https://blog.csdn.net/weixin_44035017/article/details/99480717

版权

ACM 专栏收录该内容

46 篇文章 3 订阅

订阅专栏

LCA(最近公共祖先)

在这里插入图片描述
首先区别祖先和父亲节点：比如4的父亲节点是2，祖先节点是2，1 。5的父亲节点是2，祖先节点是2，1

求解最近公共祖先，比如要求解4和3的最近公共祖先就是1。4和5的最近公共祖先就是2

求解最近公共祖先的方法有很多，比如最简单暴力的方法就是一个一个向上找
还有就是倍增优化，用欧拉序加上ST表。

暴力求解LCA



#include<bits/stdc++.h>
using namespace std;

const int maxn=10000+10;
vector<int> tree[maxn]; //用数组加上动态数组的方法存储输入数据
int fa[maxn];       //存结点的父亲节点
int deep[maxn];    //存节点的深度
bool find_root[maxn];  //存储当前结点有没有父亲节点
int root,n,q;

void dfs(int x){  //dfs建树
    for(int i=0;i<tree[x].size();i++){  //tree[x][0]是当前结点 tree[x][i]是当前节点的儿子节点
      int y=tree[x][i];  //取出儿子节点y
      deep[y]=deep[x]+1; //儿子节点y的深度等于父亲节点的深度加1
      fa[y]=x;   //y节点的父亲节点是X；
      dfs(y);  //然后继续递归dfs儿子节点
    }
}

void init(){  //预处理
    for(int i=1;i<=n;i++){  //找到根节点  根据find_root数组找，因为根节点没有父亲节点，所以是存的是false
      if(!find_root[i]){  
        root=i;
        break;
      }
    }
    deep[root]=1;  //初始化根节点的深度
    fa[root]=root;  //根节点的父亲节点是他本身
    dfs(root);  //根据根节点dfs建树
}

int lca(int x,int y){   //搜索  
   while (deep[x]>deep[y]) x=fa[x];   //首先要先将要查询的两个节点的深度弄成一样
   while (deep[x]<deep[y]) y=fa[y];
   while(x!=y){   //深度一样判断他们两是不是一样的，如果一样的说明就找到最近公共祖先了
     x=fa[x];
     y=fa[y];
   }
   return x;
}

int main(){
   scanf("%d %d",&n,&q);
   memset(find_root,false,sizeof(find_root));
   int u,v;
   for(int i=1;i<n;i++){
      scanf("%d %d",&u,&v);
      tree[u].push_back(v);
      find_root[v]=true;
   }
   init();
   while(q--){
       scanf("%d %d",&u,&v);
       printf("%d\n",lca(u,v));
   }
   return 0;
}

倍增优化

暴力求解lca存在的问题就是他一个一个的往上移就会存在时间复杂度很高的问题
所以就需要进行优化，这就用的倍增的思想
比如求9和3的公共最近祖先。可以让9跳着往上走，比如9先往上跳1就跳到节点7，9往上跳2就跳到节点5，9往上跳4就跳到节点1。然后让3往上走1就跳到了节点1。这样9就只跳了3次就找到了公共节点。时间复杂度低了很多
然后他这个跳多上步就是运用了二进制的思想，跳1就是2的0次方，跳2就是2的1次方，跳4就是2的2次方，以此类推
在这里插入图片描述
知道了怎么跳，我们就把他存起来，在查询的时候直接跳到那一步。
上图中，最左边那一列就是节点编号1到9(也是二维数组的行下标) ，最上面的0 1 2对应的就是2的多少次方，1 2 4就是跳的步数。存储的时候是没有0 1 2和 1 2 4那两行的。
然后数组anc[i][j]就表示的第i个节点跳2的j次方时的节点编号


#include<bits/stdc++.h>
using namespace std;
const int maxn=10000+5;
vector<int> tree[maxn];
int anc[maxn][25];  
int fa[maxn];
int deep[maxn];
bool find_root[maxn];

int root,n,q;

void dfs(int x){ //dfs建树
  anc[x][0]=fa[x];//走一步也就是他父亲结点的值
  for(int i=1;i<=22;i++){  //这里用22是因为计算机能储存的大小的限制，用22就能遍历跳完整个树
    anc[x][i]=anc[anc[x][i-1]][i-1];  //动态规划的方法
    //比如9跳4步(2的2次方)为1就等于5跳两步(2的1次方)的值，两个次方刚好相差1，就是i-1； 
  }
  for(int i=0;i<tree[x].size();i++){  
        int y=tree[x][i];   
        fa[y]=x;
        deep[y]=deep[x]+1;
        dfs(y);   
  }
}

void init(){
   for(int i=1;i<=n;i++){
      if(!find_root[i]){
        root=i;
        break;
      }
   }
   deep[root]=1;
   fa[root]=root;
   dfs(root);
}

int lca(int x,int y){   
    if(deep[x]<deep[y]) swap(x,y);  //默认x的深度更大
    for(int i=22;i>=0;i--){
       if(deep[y]<=deep[anc[x][i]]){  //x往前跳
           x=anc[x][i];
       }
    }
    if(x==y) return x;  
    for(int i=22;i>=0;i--){
       if(anc[x][i]!=anc[y][i]){  //一直跳到两个节点相等
          x=anc[x][i];
          y=anc[y][i];
       }
    }
    return anc[x][0];
}

int main(){
   scanf("%d %d",&n,&q);
   memset(find_root,false,sizeof(find_root));
   int u,v;
   for(int i=1;i<n;i++){
      scanf("%d %d",&u,&v);
      tree[u].push_back(v);
      find_root[v]=true;
   }
   init();
   while(q--){
     scanf("%d %d",&u,&v);
     printf("%d\n",lca(u,v));
   }
   return 0;
}

欧拉序+ST表

求解区间最值（RMQ）

1.ST表(
st表用于求解区间内的一个东西，比如求解区间最值
它是解决RMQ问题(区间最值问题)的一种强有力的工具
它可以做到O(nlogn)预处理，O(1)查询最值
ST表是利用的是倍增的思想

在这里插入图片描述
上面就是ST表比如我要求解5到9的区间最值，就只用求解5到1的区间最值是8，8到9的区间最值是9，然后比较8和9那个更大，显然是9。所以5到9的区间最值就是9
你会发现5到9区间的最值就是求解5到1区间和8到9区间的两个最值，然后5到1区间和8到9区间是有交集的这就保证整出两个有交集的子集就能整出这两个子集的区间最值去比较就行了
然后我用动态规划的方法去建立ST表
F[i,j]表示左端点为i，长度为2的j次方这样一个区间的最值，实际上就是区间【i，i+2^(j-1) 】
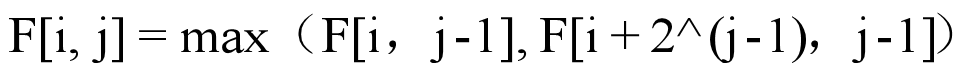
在这里插入图片描述
比如F[5,3]=max(F[5,2],F[9,2])
就代表max(5到12区间) =max(max(5到8),max(9到12))

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int maxn=1000000+10;
int num[maxn][25];
int a[maxn];
int n,q;

void ST(){
   int l=int(log((double)n)/log(2.0));  //区间长度用二进制去倍增，所以我的最大区间长度只需logn/log2 取整  比如区间长度为６　只需最大为２的２次方为４
   for(int j=1;j<=l;j++){  //枚举长度（也就是枚举次方）
     for(int i=1;i+(1<<(j-1))-1<=n;i++){  //枚举端点 1<<j表示2的J次方　
        num[i][j]=max(num[i][j-1],num[i+(1<<(j-1))][j-1]);　 //利用二进制拆成两个区间
      }
   }
}

int rmq(int l,int r){  //查询
   int k=int(log((double)(r-l+1))/log(2.0));　　
   return max(num[l][k],num[r-(1<<k)+1][k]);  //查询时利用二进制 用两个相交的子集整出各自子区间的最值然后比较
}
int main(){
   int x,y;
   scanf("%d %d",&n,&q);
   for(int i=1;i<=n;i++){
      scanf("%d",&a[i]);
      num[i][0]=a[i];
   }
   ST();
   while(q--){
      scanf("%d %d",&x,&y);
      printf("%d\n",rmq(x,y));
   }
return 0;   
}

欧拉序+ST表求解LCA

欧拉序（前序遍历得到的序列，叫dfs序，但数字可以重复出现，一进一出，叫欧拉序），会发现根结点总在中间，而根结点是该段序列深度最小的点
因此两个点的LCA，就是在该序列上两个点第一次出现的区间内深度最小的那个点

在这里插入图片描述

求区间最值得时候我们可以使用ST表去存子区间的最值，所以我们可以改进一下，将存储最值改成根据区间中深度最小来存储最近公共祖先不就可以了

那如何确立两个点查询时的区间呢，我们只需找到欧拉序里第一个出现此节点的下标即可。
然后存起来

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

const int maxn=10010;
vector<int> tree[maxn];
struct node{
  int deep;
  int m;  //节点编号
}a[maxn<<2],num[maxn<<2][25];
//a存的是欧拉序 num是st表

int first[maxn];   //存每个节点第一次出现的cnt
int deep[maxn];   //深度
bool find_root[maxn];

int root,n,q;
int cnt;  //下标

node calc(node a,node b){  //比较函数 返回深度更小的
   if(a.deep<b.deep) return a;
   return b;
}

void  dfs(int x){  //dfs初始化欧拉序
    first[x]=cnt;
    if(tree[x].size()==0){
       a[cnt].m=x;
       a[cnt++].deep=deep[x];
    }
    for(int i=0;i<tree[x].size();i++){
       int y=tree[x][i];
       deep[y]=deep[x]+1;
       a[cnt].m=x;
       a[cnt++].deep=deep[x];
       dfs(y);
    }
} 

void ST(){
      int l=int(log((double)cnt)/log(2.0));
      for(int j=1;j<=l;j++){
           for(int i=1;i+(1<<(j-1))-1<=cnt;i++){
              num[i][j]=calc(num[i][j-1],num[i+(1<<(j-1))][j-1]);  //含义和区间最值查询一样，不过这里存的是深度最小的节点
           }
      }
}

void init(){  //预处理
    for(int i=1;i<=n;i++){
       if(!find_root[i]){
         root=i;
         break;
       }
    }
    cnt=1;  //欧拉序的下标
    deep[root]=1;
    dfs(root);  
    for(int i=1;i<=cnt;i++){
       num[i][0]=a[i];
    }
    ST();  //建立ST表
}

int rmq(int l,int r){  //查询
  l=first[l];  //先根据节点找区间
  r=first[r];
  if(l>r) swap(l,r);
  int k=int(log((double)(r-1+1))/log(2.0));
  return calc(num[l][k],num[r-(1<<k)+1][k]).m;
}

int main(){
   int x,y;
   scanf("%d %d",&n,&q);
   memset(find_root,false,sizeof(find_root));
   for(int i=1;i<n;i++){
      scanf("%d %d",&x,&y);
      tree[x].push_back(y);
      find_root[y]=true;
   }
   init();
   while(q--){
      scanf("%d %d",&x,&y);
      printf("%d\n",rmq(x,y));
   }
}

ReverieZH

关注

3
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
LCA(最近公共祖先)+RMQ(区间最值)详解

LCA(最近公共祖先)首先区别祖先和父亲节点：比如4的父亲节点是2，祖先节点是2，1 。5的父亲节点是2，祖先节点是2，1求解最近公共祖先，比如要求解4和3的最近公共祖先就是1。4和5的最近公共祖先就是2求解最近公共祖先的方法有很多，比如最简单暴力的方法就是一个一个向上找还有就是倍增优化，用欧拉序加上ST表。暴力求解LCA#include<bits/stdc++.h&...
复制链接

扫一扫