Leetcode 207. Course Schedule + Leetcode 210. Course Schedule II（详细题解）

最新推荐文章于 2021-09-04 09:59:00 发布

rain_Man2018

最新推荐文章于 2021-09-04 09:59:00 发布

阅读量237

点赞数

分类专栏： leetcode 文章标签：拓扑排序 bfs

本文链接：https://blog.csdn.net/weixin_44038165/article/details/100726864

版权

leetcode 专栏收录该内容

17 篇文章

订阅专栏

Leetcode 207. Course Schedule

1：题意

你需要上n个课程，标记为0~n-1，有些课程有前导课，比如你要上课程0必须先上课程1，我们用一个整数对[0,1]来表示。
给出课程的总数和一系列的课程先导关系对，判断是否可能上完所有的课程！

2：输入输出

输入：2, [[1,0]]
输出：True
分析：共有2个课程，你需要先上课程0再上课程1，因此是可能的

输入：2, [[1,0],[0,1]]
输出: False
分析：共有2个课程，你需要先上课程0再上课程1，而且上课程1之前你必须先上课程0，因此这是不可能的。

3: 思路

引入拓扑排序的概念：
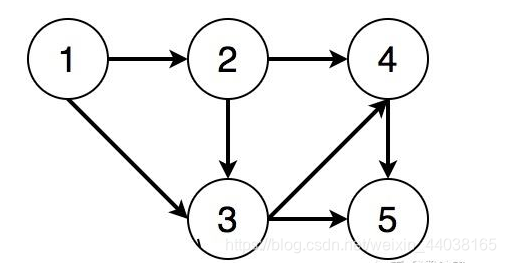
在这里插入图片描述
如上图所示：有5门课程，编号为1-5，选修课程5的时候必须先修课程3和4，选修课程4之前必须先修课程2和3，选修课程3之前必须选修课程1和2，选修课程2之前必须选修课程1，因此应该从课程1开始选课，然后才能顺利地把所有课程修完。

从上图可知，这个问题等价于判定一个有向图中是否存在环。如果存在环，就不存在拓扑序，也就是不可能上完所有的课程。

拓扑排序可以用广度优先搜索来实现。

因此算法的步骤是：
第一：数据预处理，将输入的[[1,2],[2,3]]这种二维数组转化为图中的邻接表
第二：记录每一个节点的入度（入度是其他节点过来的箭头指向本身的个数）
第三：寻找入度为0的点，这个点对应的课程就是最开始修的课程
第四：去掉入度为0的点，修改这个点指向其他节点的箭头个数，即修改其他节点的入度
第五：重复步骤三和步骤四，把图化简到null就输出True,否则输出False

四：算法实现（python）

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        graph = collections.defaultdict(list)  #建立邻接表 1:[0]表示先学课程1，再学课程0
        inDegree = [0] * numCourses # 记录每一门课的入度，表示先修课程的门数
        for pair in prerequisites:
            graph[pair[1]].append(pair[0])
            inDegree[pair[0]] += 1
        
        for i in range(numCourses):
            circle = False  # 记录是否有入度为0的点
            for j in range(numCourses): # 找到一个入度为0的点作为遍历的起始点
                if inDegree[j] == 0: 
                    circle = True
                    break
            if not circle: return False  # 所有节点的入度都大于0，说明有环
            inDegree[j] = -1 # 这个入度为0的节点访问过了，不会再重复访问了
            
            for v in graph[j]: # 去掉入度为0的点和，邻接节点的入度减1
                inDegree[v] -= 1
        
        return True

Leetcode 210. Course Schedule II

1：题意

你需要上n个课程，标记为0~n-1，有些课程有前导课，比如你要上课程0必须先上课程1，我们用一个整数对[0,1]来表示。
给出课程的总数和一系列的课程先导关系对，返回你修完所有课程的顺序，结果可能有多种，只需要返回其中的一种即可。

2：输入输出

Input: 2, [[1,0]]
Output: [0,1]

Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]

3：思路

从Leetcode 207. Course Schedule的思路上可知，在每次选择入度为0的点的时候只要记录一下这个点，然后返回先后顺序下找到的入度为0的点的列表就是本题的答案！

4：算法实现（python）

class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        graph = collections.defaultdict(list)
        indegree = [0] * numCourses
        res = []
        
        for pair in prerequisites:  # 建立邻接表
            graph[pair[1]].append(pair[0])
            indegree[pair[0]] += 1
        
        for i in range(numCourses):
            no_circle = False 
            for j in range(numCourses): # 寻找入度为0的节点
                if indegree[j] == 0:
                    no_circle = True
                    break
            if not no_circle: return []
            
            res.append(j) # 把入度为0的点记录下来
            indegree[j] = -1 # 把入度为0的点标记访问了
            
            for k in graph[j]:  # 修改入度为0的相邻节点的入度
                indegree[k] -= 1
        
        return res