图的遍历和从Shortest path tree 问题

本文章是关于CS61b课程的部分算法总结

图的定义：

图由一系列节点和边组成，每个边连接两个节点，由一条边连接的节点称为相邻结点。其中如果一个图满足以下条件：边不可以两端连接同一个结点（不能有节点连接自身）；不能有两根边连接两个相同节点（即两节点平行），则称为该图为simple graph（简单图）。（注：所有的树结构都是图）

另外，如下所示，图分为有向图和无向图。

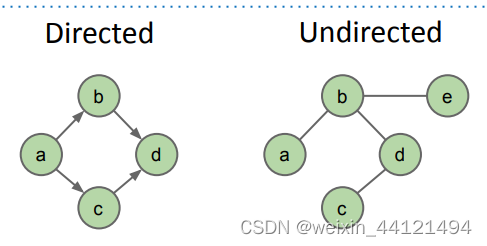
图的遍历

图的遍历是图最常见的一种算法，用于解决节点相连等问题。遍历主要分为深度优先遍历、广度优先遍历，

深度优先遍历（Depth-First Traversal）：

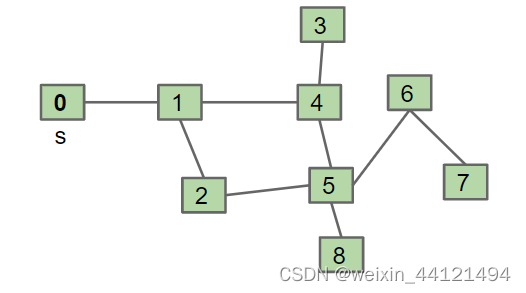
从一个图中某个顶点V出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和V有路径相通的顶点都被访问到。深度优先遍历针对一个邻居，总是优先遍历这个邻居的到最深处。如下图所示，如果从0开始遍历，如果一个节点有多个子节点，那么总是优先遍历数值较小的节点，那么下图使用DFT的遍历顺序如下：

0——1——2——5——4——3

到达3之后由于没有未被遍历的相邻节点了，所以向上找，找到5，然后继续遍历

6——7，同样的，再次向上，最后遍历8。遍历结束。

广度优先遍历（BreadthFirstTraversal）：

指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

如下图所示，如果从0开始遍历，如果一个节点有多个子节点，那么总是优先遍历数值较小的节点，那么下图按照BFT的访问顺序则为 

0——1——2——4——5——3——6——8——7

最短路径

对于边的权重不同可以为边添加weight数值，如下所示。如果对于这样的图，想要找从一点s到另一点t的权重最短的路径，称为最短路径问题（shortest path）。解决方法有Dijkstra’s 算法和 A*算法。

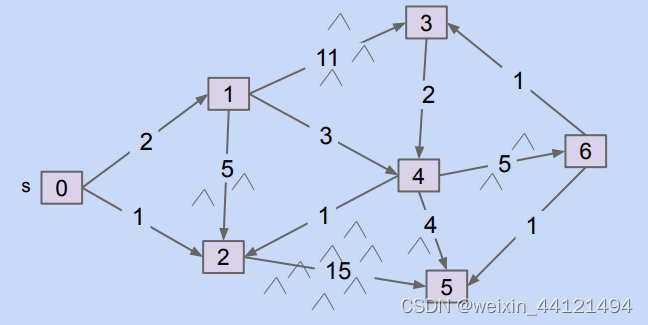
Dijkstra’s 算法：

从一个节点出发，道道其余所有节点的最短路径是一个树结构，称之为最短路径树。最短路径树种访问每个节点的路径都是唯一的，且是最短的。Dijkstra的算法如下：首先需要一个节点距离出发点的距离d数据，一个一个在最短路径树中的上一个节点数据，即为edgeTo

1、初始化所有节点距离远点的距离数据D，出发点s的距离为0，其余为正无穷。并将edgeTo 设为null。

2、从队列中取出最近的结点（第一次即S），计算该结点到其相邻结点的距离。

3、将该距离加上其与相邻节点间的距离则为相邻节点到原点的距离，比较该如果比已经有的数据更近，则更新该数据并重新排序。然后更新edgeTo的数据，将edgeto设为2中取出的节点。

4、重复上述过程直至所有节点都被访问到。

故上图的遍历结果如下：初始化后，从中取出S，距离为0，更新其相邻节点1，2的数据，更新后如下 

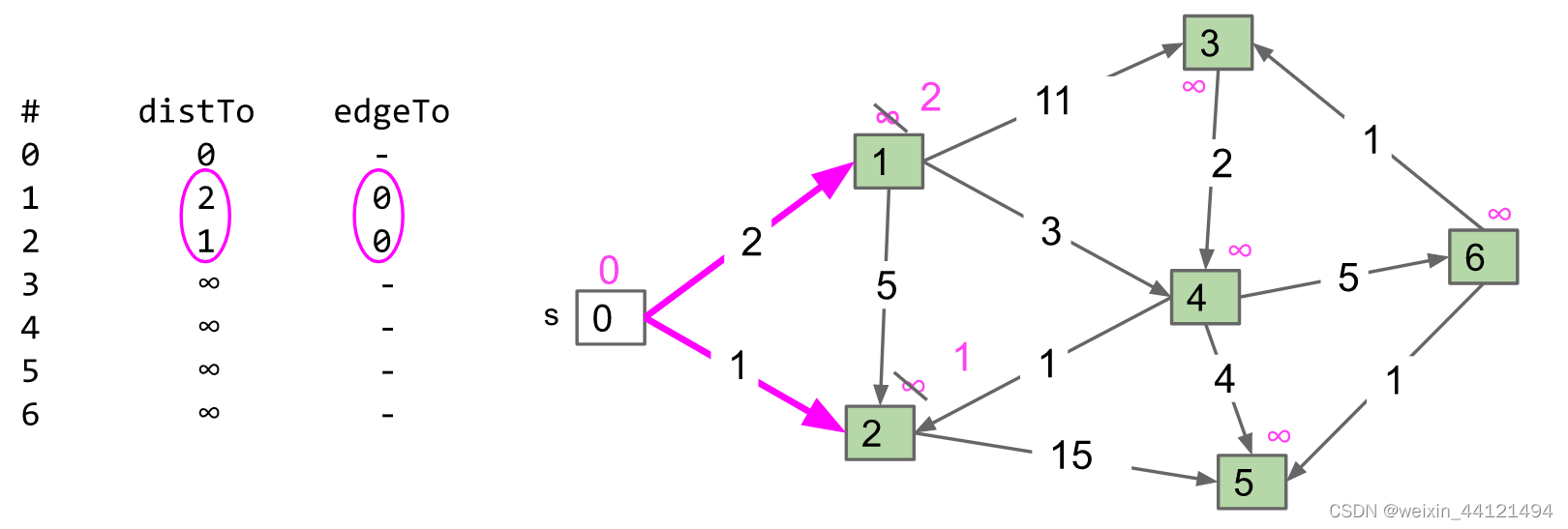
计算s到其下属结点的距离，到1的d 为2，到2的d为1，更新该数据，并排序；

现在距离最小的为1，结点2，计算2到期下属结点的距离并更新，2到5的距离为15，故更新5经到出发点的距离为1+15 = 16< 正无穷。 故更新5的数据，d = 16，edgeTo = 2并排序。

现在距离s最近的是结点1，距离为2，将其拿出并计算。其到下苏3，4，2的距离更新并计算。

1到2：2+5>1，不更新

1到3：2+11<无穷，更新，D = 2+11 = 13，edgeTo 改为1，同理4也更新，d = 2+3 = 5，edgeTo改为1.

现在距离s的最短结点为4，，距离为5，故更新到5，6的距离和edgeTo：

5没有下属结点，将6拿出，更新3，得到全部结点。获得shortest path tree。

全部遍历结束后的结果：

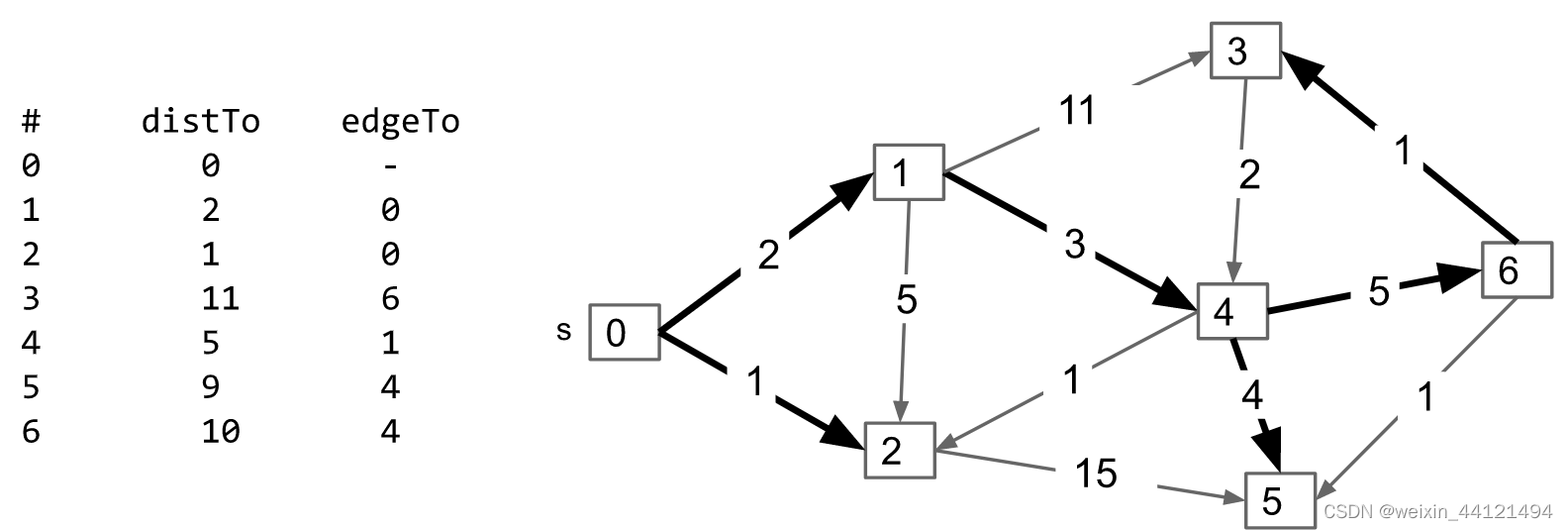
这样就根据Dijkstra算法得到了最短路径树，也就解决了开头提出的从一个节点到达其他节点的最短路径问题。

 A*算法

相比于Dijkstra算法，A*算法引入了评价函数估计函数H()的概念，该函数能够基于其他算法估计一个节点与目标节点之间的距离。其准确性不高。

下图中H即为节点v，距离goal之间的距离，和dijkstra类似的，将从0出发到达节点V的距离记为D，上一个节点记为edgeto，V到目标节点的距离记为H，按照H+D的大小进行排序，从最小距离开始遍历。

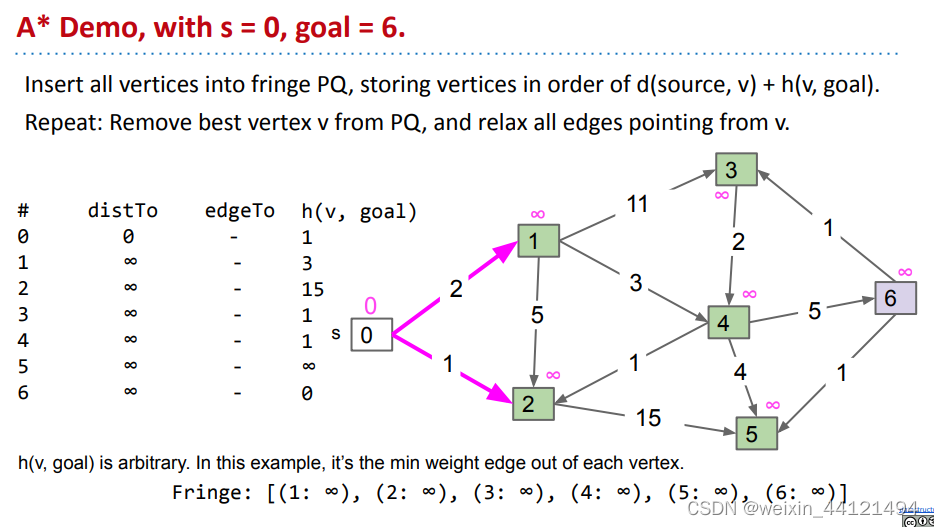
遍历结束后的更新状态为：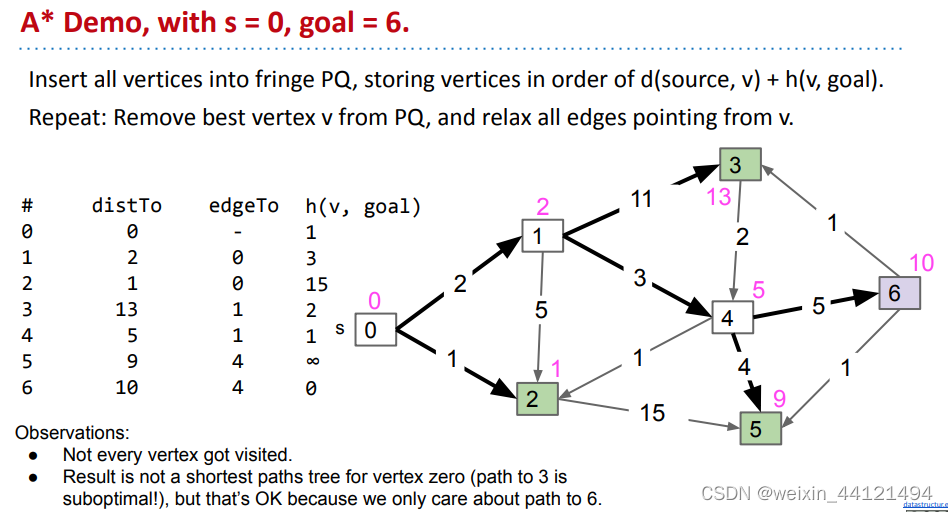

 由此就得到了从原点到达目标的最终最短路径。