1697 检查边长度限制的路径是否存在

题目描述：
给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。
给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。
请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

示例 1：

输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

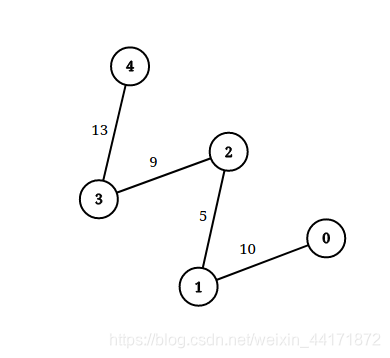
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

提示：
2 <= n <= 105
1 <= edgeList.length, queries.length <= 105
edgeList[i].length == 3
queries[j].length == 3
0 <= ui, vi, pj, qj <= n - 1
ui != vi
pj != qj
1 <= disi, limitj <= 109
两个点之间可能有 多条 边。

方法1：
主要思路：解题汇总链接
（1）使用了建图后，dfs和bfs的方法，但都超时，最后按照题解中大佬的思路，使用并查集；
（2）这里的并查集的使用，需要先根据边的权重对边进行升序排序，同时对查询的数组，根据结点的距离，也进行升序排序；
（3）在对查询的数组进行排序的时候，为了能够找到该查询原来的索引位置，这里对各个查询进行了索引的标识；
（4）在使用并查集进行边的插入时，需要先判读当前要插入的边的权重是否小于该次查询的两点之间的limit，若小于，则可以插入该边，并在循环中判断下一条边，直到当前边的长度大于等于limit；
（5）然后使用建立好的并查集关系判断查询的两点是否连通，若连通，说明满足要求，更新res；

class Solution {
public:
	//找出给定点的父节点
    int find_father(vector<int>&father,int child){
        int tmp=child;
        while(child!=father[child]){//找出父节点
            child=father[child];
        }
        while(tmp!=father[tmp]){//压缩路径
            int pre=tmp;
            tmp=father[tmp];
            father[pre]=child;
        }
        return child;//返回找到的父节点
    }
    //插入边
    void unite(vector<int>&father,int child,int parent){
        child=find_father(father,child);
        parent=find_father(father,parent);
        if(child==parent){//判断两个点直接是否已经连通了
            return;
        }
        //若之前不连通，则连通
        father[child]=parent;
    }
	//判断两个点是否连通
    bool is_connected(vector<int>&father,int child_1,int child_2){
        int father_1=find_father(father,child_1);
        int father_2=find_father(father,child_2);
        return father_1==father_2;
    }

    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
        sort(edgeList.begin(),edgeList.end(),[](const auto& lhs,const auto& rhs){//对边之间的关系进行升序排序
           return  lhs[2]<rhs[2];
        });
        for(int i=0;i<queries.size();++i){//将各次查询对应的索引位置存储
            queries[i].push_back(i);
        }
        sort(queries.begin(),queries.end(),[](auto&lhs,auto&rhs){//将查询数组按照limit进行升序排序
            return lhs[2]<rhs[2];
        });
        vector<int> father(n,0);//并查集关系的存储数组
        for(int i=1;i<n;++i){//各个结点的父节点初始化自己
            father[i]=i;
        }
        int pos=0;//插入各个边的索引
        vector<bool>res(queries.size(),false);//返回结果
        for(int i=0;i<queries.size();++i){//各次查询
            auto& q=queries[i];
            while(pos<edgeList.size()&&edgeList[pos][2]<q[2]){//判断当前边是否需要插入到并查集中
                unite(father,edgeList[pos][0],edgeList[pos][1]);//插入当前边
                ++pos;//判断下一条边
            }
            //判断当前查询的连通性
            res[q[3]]=is_connected(father,q[0],q[1]);
        }
        return res;
    }
};