UVA 11426

欧拉函数+GCD

题目大意 求下面这个

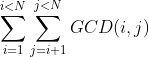
看了很多blog···感觉都讲的很不清楚（看不懂），肯定是我太弱了。

所以我决定自己写一篇，然后看看能不能在写的过程中弄清楚。

因为脑子可能没别人好用，看文字很难看出个所以然，所以我学习一般都需要例子来加以理解，我也认为这样可以让人更加清晰的理解我想表达什么。

如果有错误，不吝请教。

然后考虑一下数据范围···暴利绝对T的。

然后开始分析题目

既然不能暴利，那么能不能换一种思路？

假设f[n]=gcd(1,n)+gcd(2,n)+...gcd(n-1,n);

那么我们要求的ans[n]=f(2)+f(3)+f(4)+...+f(n);

所以我们只要把f[n]求出来就好了。

对gcd(x,n)进行分类，用a[i]表示gcd(x,n)=i的x的个数，意思就是从1~n-1中有多少个x0和x一样是gcd(x0,n)=i。

这里的m表示i的种类数目，没有别的含义。

举个例子F[6]=gcd(1,6)+gcd(2,6)+gcd(3,6)+gcd(4,6)+gcd(5,6);

但是这四个我们可以给他分类

不难发现gcd(1,6)==gcd(5,6)=1; //i=1的个数为欧拉函数φ(6);

gcd(2,6)==gcd(4,6)=2gcd(1,3)=1,gcd(2,3)=1;//此处i=2的个数也就是欧拉函数φ(3)

gcd(3,6)=3gcd(1,2)=1;//此处i=3的个数也就是欧拉函数φ(2);

然后利用数目乘以最后的i

F[6]=2*1+2*2+3*1=2+4+3=9;

那么gcd(x,n)=i,可以化简成gcd(x/i,n/i)=1.与n/i互质的个数也就是欧拉函数值φ(n/i);

通过欧拉函数找到了个数，那么这个公式不就出来了吗？

   i 表示这一类的权值，φ(n/i)则表示这一类的个数

所以最终的答案

 

题目链接:https://cn.vjudge.net/problem/UVA-11426 

AC代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long int
#define fin(a,n) for(int i=a;i<=n;i++)
#define fjn(a,n) for(int j=a;j<=n;j++)
#define fni(n,a) for(int i=n;i>=a;i--)
#define fnj(n,a) for(int j=n;j>=a;j--)
const int maxn=4e6+10;
bool vis[maxn];
int prime[maxn];
ll f[maxn];
int phi[maxn];
ll ans[maxn];
int cnt=0;
void euler()//欧拉筛欧拉函数
{   phi[1]=1;//注意，欧拉函数1要单独判断
	memset(vis,true,sizeof(vis));
	vis[1]=false;
	fin(2,maxn)
	{
		if(vis[i])
		{
			prime[++cnt]=i;
			phi[i]=i-1;//欧拉函数特性一
		}
		for(int j=1;j<=cnt&&prime[j]*i<=maxn;j++)
		{
			vis[i*prime[j]]=false;
			if(i%prime[j]==0)
			{
				phi[i*prime[j]]=phi[i]*prime[j];//欧拉函数是可积函数，特性二
				break;
			}
			phi[i*prime[j]]=phi[i]*phi[prime[j]];//欧拉函数特性三
		}
	}
}
int main()
{   ll n;
	euler();
	fin(1,maxn)
	{
		for(int j=i+i;j<=maxn;j+=i)
		f[j]+=i*phi[j/i];//找出F[n]
	}
	fin(1,maxn)ans[i]=ans[i-1]+f[i];//打表答案
	while(~scanf("%lld",&n))
	{   if(n==0)break;
		printf("%lld\n",ans[n]);
	}
	return 0;
 }