matlab使用教程(5)—矩阵定义和基本运算

        本博客介绍如何在 MATLAB 中创建矩阵和执行基本矩阵计算。

        MATLAB 环境使用矩阵来表示包含以二维网格排列的实数或复数的变量。更广泛而言，数组为向量、矩阵或更高维度的数值网格。MATLAB 中的所有数组都是矩形，在这种意义上沿任何维度的分量向量的长度均相同。矩阵中定义的数学运算是线性代数的主题。

1创建矩阵

        MATLAB 提供了许多函数，用于创建各种类型的矩阵。例如，您可以使用基于帕斯卡三角形的项创建一个对称矩阵：

A = pascal(3)

A =

1 1 1

1 2 3

1 3 6

        您也可以创建一个非对称幻方矩阵，它的行总和与列总和相等：

B = magic(3)

B =

8 1 6

3 5 7

4 9 2

        另一个示例是由随机整数构成的 3×2 矩形矩阵：在这种情况下，randi 的第一个输入描述整数可能值的范围，后面两个输入描述行和列的数量。

C = randi(10,3,2)

C =

9 10

10 7

2 1

        列向量为 m×1 矩阵，行向量为 1×n 矩阵，标量为 1×1 矩阵。要手动定义矩阵，请使用方括号 [ ] 来表示数组的开始和结束。在括号内，使用分号 ; 表示行的结尾。在标量（1×1 矩阵）的情况下，括号不是必需的。例如，以下语句生成一个列向量、一个行向量和一个标量：

 

u = [3; 1; 4]
v = [2 0 -1]
s = 7

u =

3

1

4

v =

2 0 -1

s =

7

2矩阵的加法和减法

        矩阵和数组的加减法是逐个元素执行的，或者说是按元素执行的。例如，A 加 B 之后再减去 A 又可以得到 B ：

X = A + B
Y = X - A

X =

9 2 7

4 7 10

5 12 8

Y =

8 1 6

3 5 7

4 9 2

        加法和减法要求两个矩阵具有兼容的维度。如果维度不兼容，将会导致错误：

X = A + C

Error using +

Matrix dimensions must agree.

3向量乘积和转置

        长度相同的行向量和列向量可以按任一顺序相乘。其结果是一个标量（称为内积）或一个矩阵（称为外积）：

u = [3; 1; 4];
v = [2 0 -1];
x = v*u

x =

2

X = u*v

X =

6 0 -3

2 0 -1

8 0 -4

        对于实矩阵，转置运算对 aij 和 a ji 进行交换。对于复矩阵，还要考虑是否用数组中复数项的复共轭来形成复共轭转置。MATLAB 使用撇号运算符 ( ' ) 执行复共轭转置，使用点撇号运算符 (.') 执行无共轭的转置。对于包含所有实数元素的矩阵，这两个运算符返回相同结果。示例矩阵 A = pascal(3) 是对称的，因此 A' 等于 A 。然而， B = magic(3) 不是对称的，因此 B' 的元素是 B 的元素沿主对角线反转之后的结果：

B = magic(3)

B =

8 1 6

3 5 7

4 9 2

X = B'

X =

8 3 4

1 5 9

6 7 2

        对于向量，转置会将行向量变为列向量（反之亦然）：

x = v'

x =

2

0

-1

        如果 x 和 y 均为实数列向量，则乘积 x*y 不确定，但以下两个乘积

x'*y和y'*x

        产生相同的标量结果。此参数使用很频繁，它有三个不同的名称内积、标量积或点积。甚至还有一个专门的点积函数，称为 dot。对于复数向量或矩阵 z ，参量 z' 不仅可转置该向量或矩阵，而且可将每个复数元素转换为其复共轭数。也就是说，每个复数元素的虚部的正负号将会发生更改。以如下复矩阵为例：

z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]

z =

1.0000 + 2.0000i 7.0000 - 3.0000i 3.0000 + 4.0000i

6.0000 - 2.0000i 0.0000 + 9.0000i 4.0000 + 7.0000i

        z 的复共轭转置为：

z'

ans =

1.0000 - 2.0000i 6.0000 + 2.0000i

7.0000 + 3.0000i 0.0000 - 9.0000i

3.0000 - 4.0000i 4.0000 - 7.0000i

        非共轭复数转置（其中每个元素的复数部分保留其符号）表示为 z.' ：

z.'

ans =

1.0000 + 2.0000i 6.0000 - 2.0000i

7.0000 - 3.0000i 0.0000 + 9.0000i

3.0000 + 4.0000i 4.0000 + 7.0000i

        对于复数向量，两个标量积 x'*y 和 y'*x 互为复共轭数，而复数向量与其自身的标量积 x'*x 为实数。

4矩阵乘法

        矩阵乘法是以这样一种方式定义的：反映底层线性变换的构成，并允许紧凑表示联立线性方程组。如果 A的列维度等于 B 的行维度，或者其中一个矩阵为标量，则可定义矩阵乘积 C = AB。如果 A 为 m×p 且 B为 p×n，则二者的乘积 C 为 m×n。该乘积实际上可以使用 MATLAB for 循环、 colon 表示法和向量点积进行定义：

A = pascal(3);
B = magic(3);
m = 3;
n = 3;
for i = 1:m
for j = 1:n
C(i,j) = A(i,:)*B(:,j);
end
end

        MATLAB 使用星号表示矩阵乘法，如 C = A*B 中所示。矩阵乘法不适用交换律；即 A*B 通常不等于B*A ：

X = A*B
Y = B*A

X =

15 15 15

26 38 26

41 70 39

Y =

15 28 47

15 34 60

15 28 43

        矩阵可以在右侧乘以列向量，在左侧乘以行向量：

u = [3; 1; 4];
x = A*u
v = [2 0 -1];
y = v*B

x =

8

17

30

y =

12 -7 10

        矩形矩阵乘法必须满足维度兼容性条件：由于 A 是 3×3 矩阵， C 是 3×2 矩阵，因此可将二者相乘得到 3 ×2 结果（共同的内部维度会消去）：

X = A*C

X =

24 17

47 42

79 77

        但是，乘法不能以相反的顺序执行：

Y = C*A

Error using *

Incorrect dimensions for matrix multiplication. Check that the number of columns

in the first matrix matches the number of rows in the second matrix. To perform

elementwise multiplication, use '.*'.

        您可以将任何内容与标量相乘：

s = 10;
w = s*y

w =

120 -70 100

        当您将数组与标量相乘时，标量将隐式扩展为与另一输入相同的大小。这通常称为标量扩展。

5单位矩阵

        普遍接受的数学表示法使用大写字母 I 来表示单位矩阵，即主对角线元素为 1 且其他位置元素为 0 的各种大小的矩阵。这些矩阵具有以下属性：无论维度是否兼容，AI = A 和 IA = A。原始版本的 MATLAB 不能将 I 用于此用途，因为它不会区分大小字母和小写字母，并且 i 已用作下标和复

数单位。因此，引入了英语双关语。函数

eye(m,n)

返回 m×n 矩形单位矩阵， eye(n) 返回 n×n 单位方阵。

6矩阵求逆

        如果矩阵 A 为非奇异方阵（非零行列式），则方程 AX = I 和 XA = I 具有相同的解 X。此解称为 A 的逆矩阵，表示为 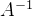。 inv 函数和表达式 A^-1 均可对矩阵求逆。

A = pascal(3)

A =

1 1 1

1 2 3

1 3 6

X = inv(A)

X =

3.0000 -3.0000 1.0000

-3.0000 5.0000 -2.0000

1.0000 -2.0000 1.0000

A*X

ans =

1.0000 0 0

0.0000 1.0000 -0.0000

-0.0000 0.0000 1.0000

        通过 det 计算的行列式表示由矩阵描述的线性变换的缩放因子。当行列式正好为零时，矩阵为奇异矩阵，因此不存在逆矩阵。

d = det(A)

d =

1

        有些矩阵接近奇异矩阵，虽然存在逆矩阵，但计算容易出现数值误差。cond 函数计算逆运算的条件数，它指示矩阵求逆结果的精度。条件数的范围是从 1 （数值稳定的矩阵）到 Inf （奇异矩阵）。

c = cond(A)

c =

61.9839

        很少需要为某个矩阵构造显式逆矩阵。当解算线性方程组 Ax = b 时，往往会错误使用 inv。从执行时间和数值精度方面而言，求解此方程的最佳方法是使用矩阵反斜杠运算符，即 x = A\b。有关详细信息，请参阅 mldivide 。

7向量范数和矩阵范数

        向量 x 的 p-范数，

        使用 norm(x,p) 进行计算。此运算是为 p > 1 的任意值定义的，但最常见的 p 值为 1、2 和 ∞。默认值为 p = 2，这与欧几里德长度或向量幅值对应：

v = [2 0 -1];
[norm(v,1) norm(v) norm(v,inf)]

ans =

3.0000 2.2361 2.0000

矩阵 A 的 p-范数，

        可以针对 p = 1、2 和 ∞ 通过 norm(A,p) 进行计算。同样，默认值也为 p = 2：

A = pascal(3);
[norm(A,1) norm(A) norm(A,inf)]

ans =

10.0000 7.8730 10.0000

        如果要计算矩阵的每行或每列的范数，可以使用 vecnorm ：

vecnorm(A)

ans =

1.7321 3.7417 6.7823

8使用线性代数方程函数的多线程计算

        对于许多线性代数函数和按元素的数值函数，MATLAB 软件支持多线程计算。这些函数将自动在多个线程上执行。要使函数或表达式在多个 CPU 上更快地执行，必须满足许多条件：

1 函数执行的运算可轻松划分为并发执行的多个部分。这些部分必须能够在进程之间几乎不通信的情况 下执行。它们应需要很少的序列运算。

2 数据大小足以使并发执行的任何优势在重要性方面超过对数据分区和管理各个执行线程所需的时间。 例如，仅当数组包含数千个或以上的元素时，大多数函数才会加速。

3 运算未与内存绑定；处理时间不受内存访问时间控制。一般而言，复杂函数比简单函数速度更快。 对于大型双精度数组（约 10,000 个元素），矩阵乘法 (X*Y) 和矩阵乘幂 (X^p) 运算符会大幅增加速度。矩阵分析函数 det 、 rcond 、 hess 和 expm 也会对大型双精度数组大幅增加速度。