查找算法【平衡二叉树】 - 平衡二叉树的删除

查找算法【平衡二叉树】 - 平衡二叉树的删除

在平衡二叉树中进行插入操作时只需从插入节点之父向上检查，发现不平衡便立即调整，调整一次平衡即可；而进行删除操作时需要一直从删除节点之父向上检查，发现不平衡便立即调整，然后继续向上检查，直到树根。

【算法步骤】

① 在平衡二叉树中查找x ，如果查找失败，则返回；如果查找成功，则执行删除操作（同二叉查找树的删除操作）。

② 从实际被删除节点之父g 出发（当被删除节点有左右子树时，令其直接前驱（或直接后继）代替其位置，删除其直接前驱，实际被删除节点为其直接前驱（或直接后继）），向上寻找最近的不平衡节点。逐层检查各代祖先节点，如果平衡，则更新其高度，继续向上寻找；如果不平衡，则判断失衡类型（沿着高度大的子树判断），并做相应的调整。

③ 继续向上检查，一直到树根。

【举个栗子】

例如，一棵二叉平衡树如下图所示，删除16。

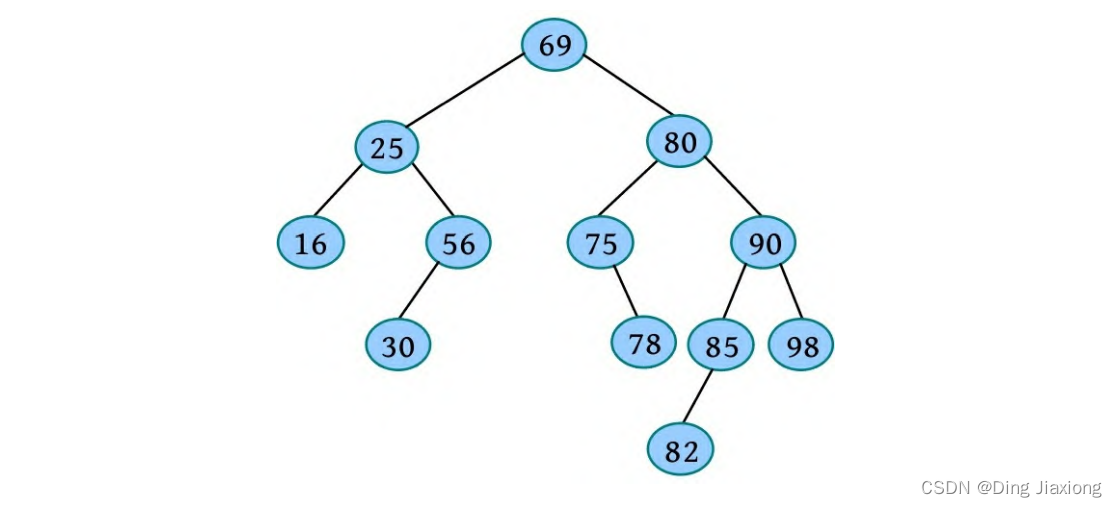
① 16为叶子，将其直接删除即可，如下图所示。

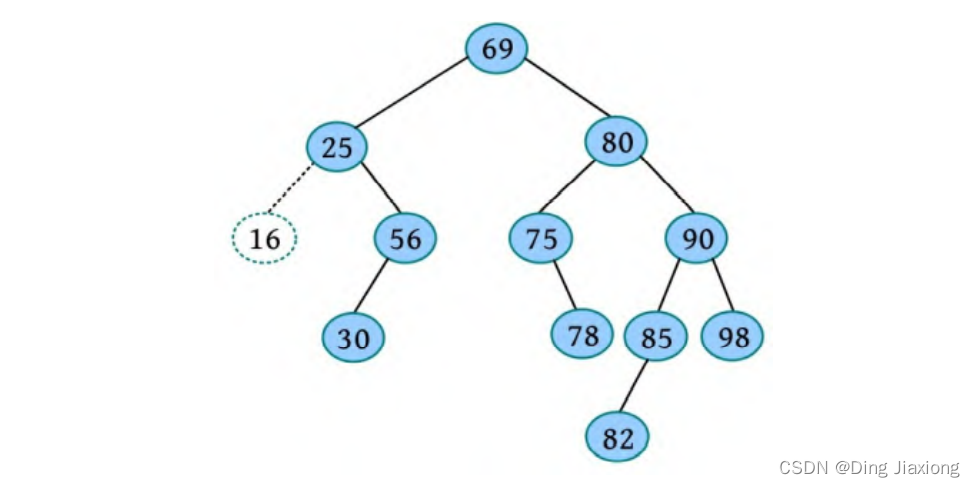
② 指针g 指向实际被删除节点16之父25，检查是否失衡，25节点失衡，用g 、u 、v 记录失衡三代节点（从失衡节点沿着高度大的子树向下找三代），判断为RL型，进行RL旋转调整平衡，如下图所示。

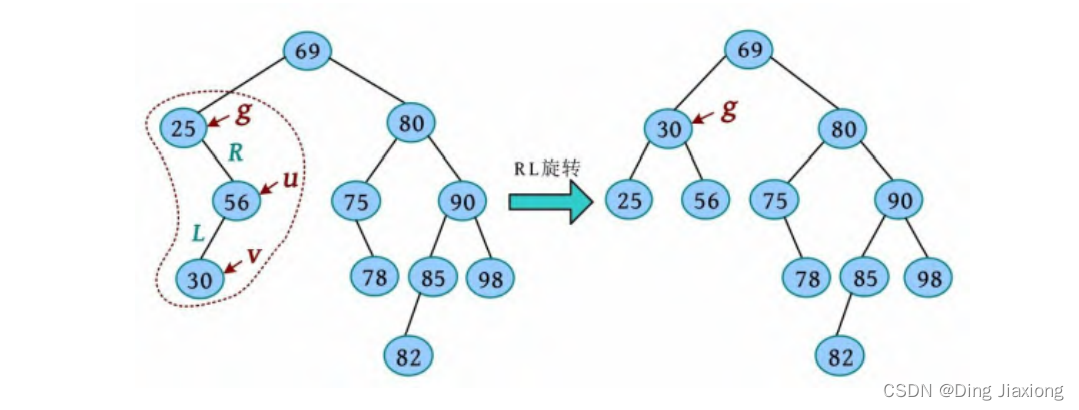
③ 继续向上检查，指针g 指向g 的双亲69，检查是否失衡，69节点失衡，用g 、u 、v 记录失衡三代节点，判断为RR型，进行RR旋转调整平衡，如下图所示。

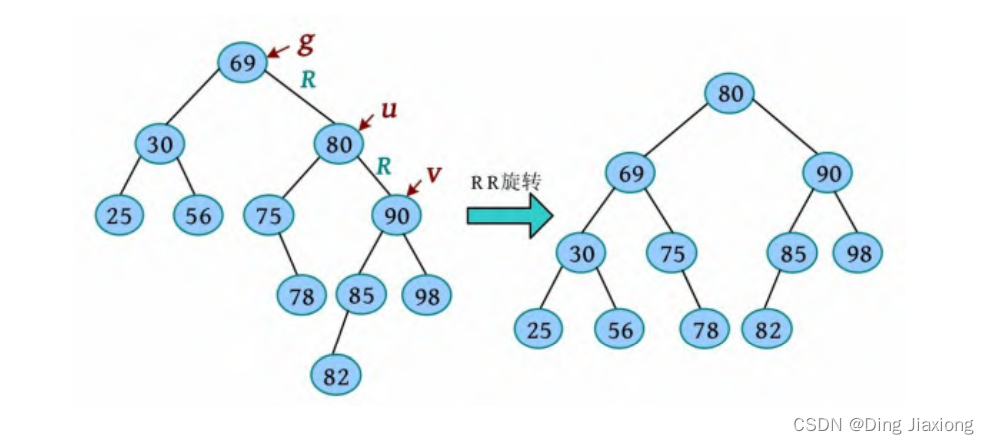
④ 已检查到根，结束。

【再一个栗子】

一棵平衡二叉树如下图所示，删除80。

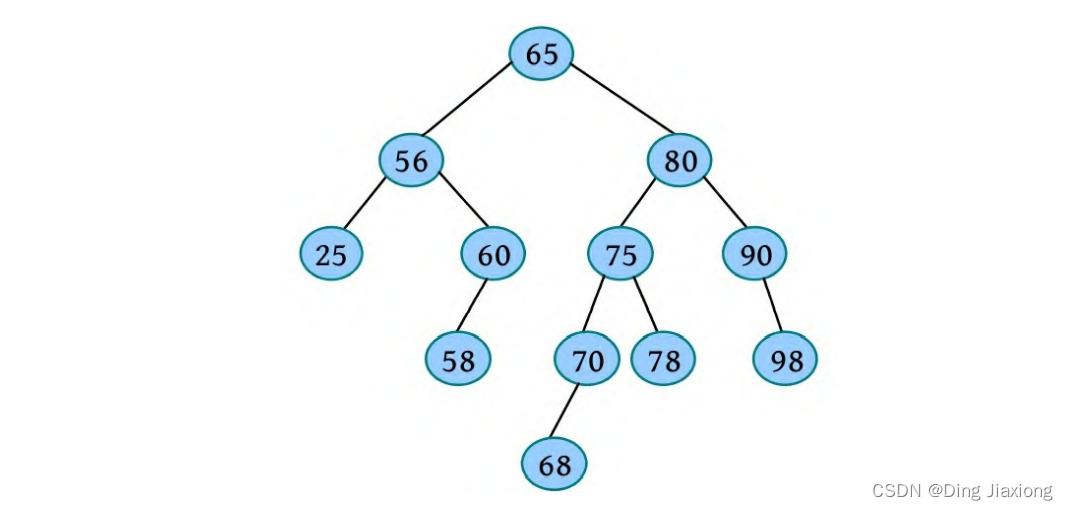
① 80的左右子树均非空，令其直接前驱78代替它，删除其直接前驱78，如下图所示。

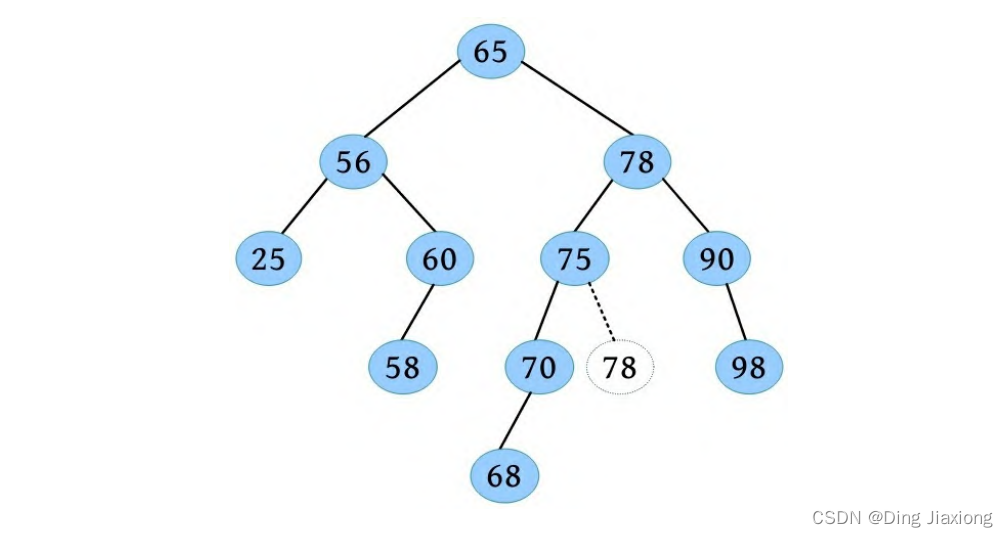
② 指针g 指向实际被删除节点78之父75，检查是否失衡，75节点失衡，用g 、u 、v 记录失衡三代节点，判断为LL型，进行LL旋转调整平衡，如下图所示。

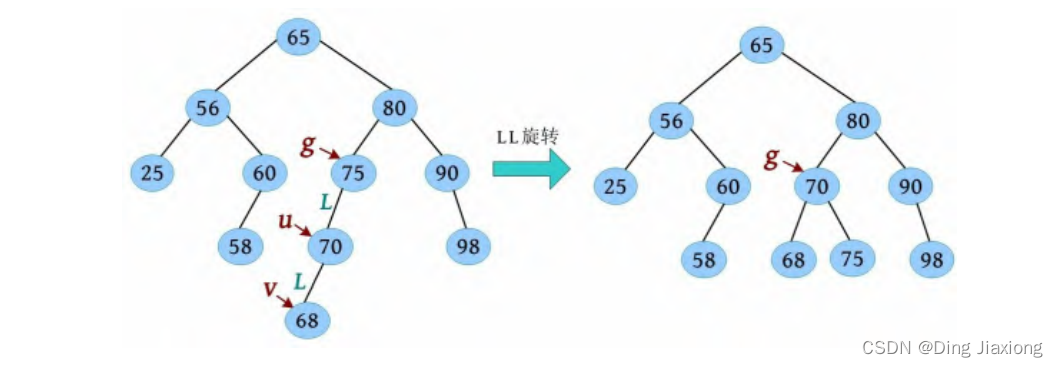
③ 指针g 指向g 的双亲80，检查是否失衡，一直检查到根，结束。

注意： 从实际被删除节点之父开始检查是否失衡，一直检查到根。

【算法实现】

AVLTree adjust(AVLTree &T){ //删除节点后，需要判断是否仍平衡，如果不平衡，则需要调整
	if(T == NULL){
		return NULL;
	}
	if(Height(T->lchild) - Height(T->rchild) == 2){ //沿着高度大的那条路径判断
		if(Height(T->lchild->lchild) >= Height(T->lchild->rchild)){
			T = LL_Rotation(T);
		}
		else{
			T = LR_Rotation(T);
		}
	}
	if(Height(T->rchild) - Height(T->lchild) == 2){ //沿着高度大的那条路径判断
		if(Height(T->rchild->rchild) >= Height(T->rchild->lchild)){
			T = RR_Rotation(T)；	
		}
		else{
			T = RL_Rotation(T);
		}
	}
	updateHeight(T);
	return T;
}

AVLTree Delete(AVLTree &T , int x){
	if(T == NULL){
		return NULL;
	}
	if(T->data == x){ //如果找到待删除节点
		if(T->rchild == NULL){ //如果该节点的右孩子为NULL，那么直接将其删除
			AVLTree temp = T;
			T = T->lchild;
			delete temp;		
		}
		else{ //否则，将其右子树的最左孩子作为这个节点，并且递归删除这个节点的值
			AVLTree temp;
			temp = T->rchild;
			while(temp->lchild){
				temp = temp->lchild;
			}		
			T->data = temp->data;
			T->rchild = Delete(T->rchild , T->data);
			updateHeight(T);
		}
		return T;
	}
	if(T->data > x){ //调整删除节点后可能涉及的节点
		T->lchild = Delete(T->lchild , x);
	}
	if(T->data < x){
		T->rchild = Delete(T->rchild , x);
	}
	updateHeight(T);
	T = adjust(T);
	return T;
}