动态规划问题的本质

网上关于动态规划的帖子有很多，但是很多讲了了半天都是让人云里雾里，没有抓到动态规划的
的本质。

其实动态规划的本质是数据结构，我们做数据结构的题，数据结构应该成为我们做题的主导思路，而不是根据题目苦思冥想数据结构应该如何构造。

就比如，DP问题就是一个DP表的填写，有的问题构造的DP表是一维的表，有的问题构造的DP表是二维的表。最终我们还是要回归到构造一个DP表来进行状态转移，所以我们可以一开始就考虑DP表的构造。

所以，动态规划问题就可以归结为DP表的构建问题了。

1.一维DP表的构建

题目:

给定不同面额的硬币 coins 和金额 amount，计算凑成总金额所需的最少的硬币个数

输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1

看到这个问题我们我们首先想到的是用一个一维数组来存储结果，这个一维数组可以用
vectorVecDp表示，这个数组里面存的值可以用来表示结果，这个数组的下标可以用来表示金额，比如：
VecDp[0]=0表示金额是0，最少硬币是0；
VecDp[1] = 1 表示金额是1，最少硬币是 1；
VecDp[2]= 1 表示金额是2，最少硬币是1；
VecDp[3] = 2 表示金额是3，最少硬币是 2；
VecDp[4]=2 表示金额是4，最少硬币是2；
VecDp[5] = 1 表示金额是5，最少硬币是 1；
VecDp[6]= 2 表示金额是6，最少硬币是2；
VecDp[7] = 2 表示金额是7，最少硬币是 2；
…
以此类推

那么这个所谓的状态转移方程怎么确定呢？有了上面的VecDp就非常简单了。
以VecDp[7]为例，VecDp[7]的前一个状态可能为VecDp[7-1]、VecDp[7-2]、VecDp[7-5]；
而VecDp[7]为什么最终是2呢？
那是因为
VecDp[6]+1=3
VecDp[5]+1 =2
VecDp[2]+1 =2
很明显2是里面最小的结果。
所以状态转移方程就非常容易得到了

min{VecDp[n-1]+1,VecDp[n-2]+1,VecDp[n-5]+1}

后面用代码表示出来这个状态转移方程就非常容易了；
下面是示例代码

#include<iostream>
#include<vector>
using namespace std;
int value[3]={1,2,5};
int main()
{
   vector<int>dp(12,0);
    for(int i=1;i<12;i++)
    {
        int min_a=1000;
        for(int j=0;j<3;j++)
        {
            if(value[j]<=i && dp[i-value[j]]+1<min_a)
                min_a = dp[i-value[j]]+1;
        }
        dp[i] = min_a;
    }
    for(int i=0;i<12;i++)
        cout<<dp[i]<<' ';
​
    return 0;
}

1.二维DP表的构建

题目：
背包问题：
有 n 个物品和一个承重为 m 的背包. 给定数组 W表示每个物品的重量和数组 V 表示每个物品的价值。问最多能装入背包的总价值是多大?

例如：

n=5，m = 10, W = [2, 2, 6, 5,4], V = [6, 3, 5, 4，6]

结果为：15

看到这个问题我们我们首先想到的是用一个二维数组来存储结果，这个二维数组可以用
vector<vector>VecDp表示,而这个二维数组的行列各表示什么呢？
我们可以把这个二维数据的行表示n,列表示m,表格如下：

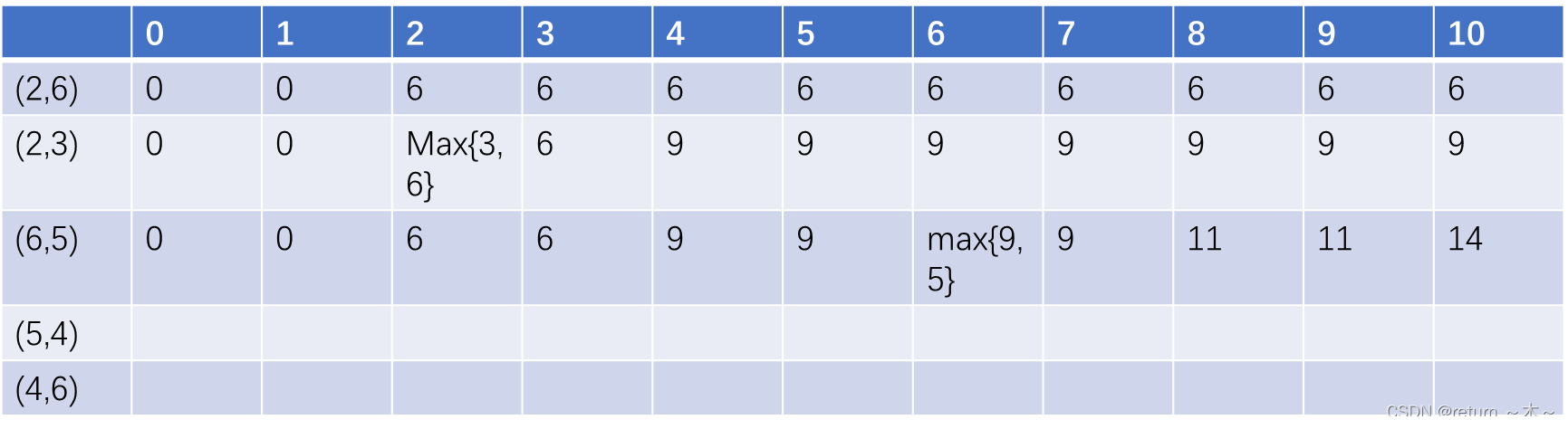
从上面的表格我们分析一下

VecDp[0][2]=0表示承重为2，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][3]=0表示承重为3，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][4]=0表示承重为4，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][5]=0表示承重为5，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][6]=0表示承重为6，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][7]=0表示承重为7，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][8]=0表示承重为8，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][9]=0表示承重为9，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[0][10]=0表示承重为10，背包里面只有（2，6）这个物品，最大总价值是6；
VecDp[1][2]=0表示承重为2，背包里面有（2，6）（2，3）这个两个物品，最大总价值是6；
VecDp[1][3]=0表示承重为3，背包里面有（2，6）（2，3）这个两个物品，最大总价值是6；
VecDp[1][4]=0表示承重为4，背包里面有（2，6）（2，3）这个两个物品，最大总价值是9；
VecDp[1][5]=0表示承重为5，背包里面有（2，6）（2，3）这个两个物品，最大总价值是9；
…
二维DP表构建好以后，那么状态转移方程怎么确定呢？有了上面的VecDp就非常简单了。
以VecDp[2][6]为例，VecDp[2][6]的前一个状态为VecDp[1][6]；那么VecDp[1][6]这个状态和谁进行比较呢？当然是和VecDp[1][0]+5进行比较啦，这个VecDp[1][0]表示把这个重为6的物品放入包之后，而5是个重为6的东西的价值。于是通过VecDp[2][6]我们得到状态转移方程

max{VecDp[i-1][j],VecDp[i][j-w[i]]+v[i]}

很明显这里里面有个限定条件是j>w[i],如果j<w[i]呢？那就更明显了，以VecDp[2][5]为例，直接和VecDp[1][5]一样，因为物体重为6，5装不下，所以直接转移到了VecDp[i-1][j];

后面用代码表示出来这个状态转移方程就非常容易了；
下面是示例代码

#include<iostream>
using namespace std;
#include<vector>
int main()
{
    int n=5,m=10;
    int w[5] = {2, 2, 6, 5,4};
    int v[5] = {6, 3, 5, 4,6};
    vector <vector<int>>dp(5, vector<int>(11, 0));
    for(int i=0;i<n;i++)
    {
        for(int j=1;j<m+1;j++)
        {
            //第一行没有上一行,所以如果能放得下,直接赋值.
            if(i==0)
            {
                if(j>=w[i])
                    dp[i][j]=v[i];
                continue;
            }
            //状态转移方程
            dp[i][j] = j>=w[i]? max(dp[i-1][j-w[i]]+v[i],dp[i-1][j]) : dp[i-1][j];
​
            //cout<<dp[i][j]<<" ";
        }
        //cout<<endl;
    }
​
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m+1;j++)
        {
            cout<<dp[i][j]<<" ";
        }
        cout<<endl;
    }
​
    return 0;
}