欧几里得空间是从二维和三维空间推广到有限n维空间的概念，它定义了内积、距离和角度。内积是向量长度与其夹角余弦的乘积，可以用来计算角度和距离。例如，两个向量的内积等于它们对应元素相乘的和，而两点间的距离是它们坐标差的平方和的平方根。这些基本概念构成了高维空间的几何基础。
欧几里得空间就是在对现实空间的规则抽象和推广（从n<=3推广到有限n维空间）。
欧几里得几何就是中学学的平面几何、立体几何，在欧几里得几何中，平行线任何位置的间距相等。而中学学的几何空间一般是2维，3维（所以，我们讨论余弦值、点间的距离、内积都是在低纬空间总结的），如果将这些低维空间所总结的规律推广到有限的n维空间，那这些符合定义的空间则被统称为欧几里得空间（欧式空间，Euclidean Space）。而欧几里得空间主要是定义了内积、距离、角（没错，就是初中的那些定义），理解了这些再去理解数学定义就很明确了。
计算两个向量的内积（对应点相乘再加总）：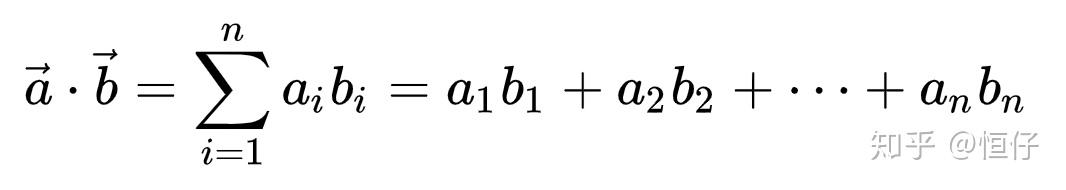
两个向量内积的计算内积的几何概念是两个向量的长度与它们夹角余弦的积，所以，内积可以表示成：
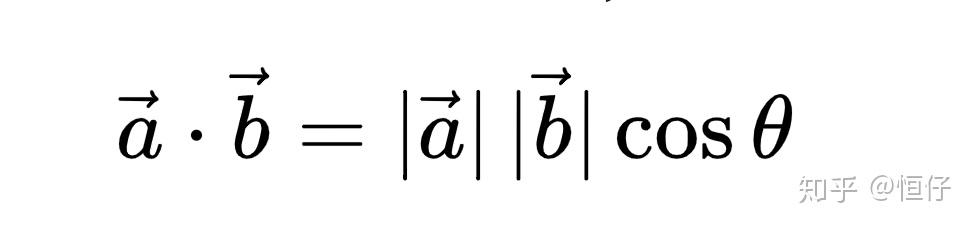初中公式：内积于是余弦值就是：
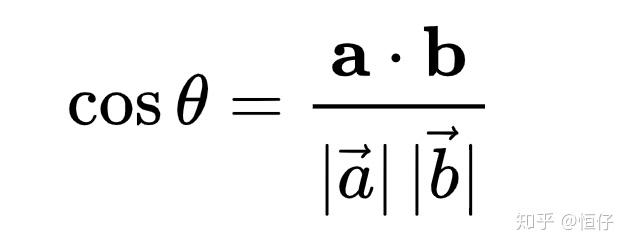初中定义：余弦值所以角的计算就是：
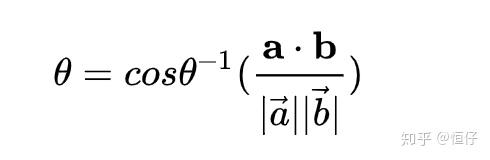角的定义计算两点x, y间的距离：
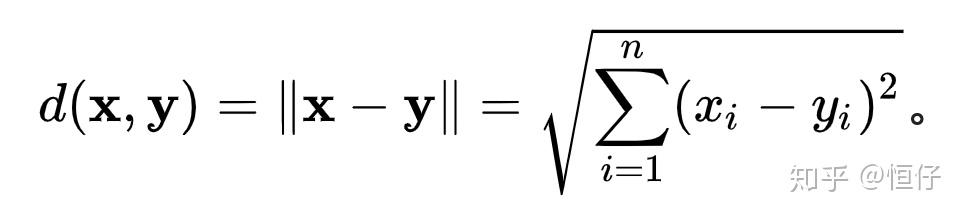点坐标之间对应相减平方加总开根号
引用来自链接：https://www.zhihu.com/question/27903807/answer/699570097
扫一扫
1514
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
