数据结构与算法之时间、空间复杂度

数据结构与算法之时间、空间复杂度
数据结构是指计算机存储、组织数据的方式，比如代码内使用数组、队列、链表、栈等来存储和操作数据就是数据结构。按存储顺序来看可分为线性和非线性，线性结构如线性表、数组、栈、队列，非线性结构如多维数组、树、图等。我的理解是把线性结构看成绳子一样，它的结构是连续的有规则可循，比如从左到右，从上到下，关系是一对一。非线性反之关系是多对一。树的结构有左子数和右子树，有两个后驱节点，图也是有多个后驱或前驱节点。如图所示


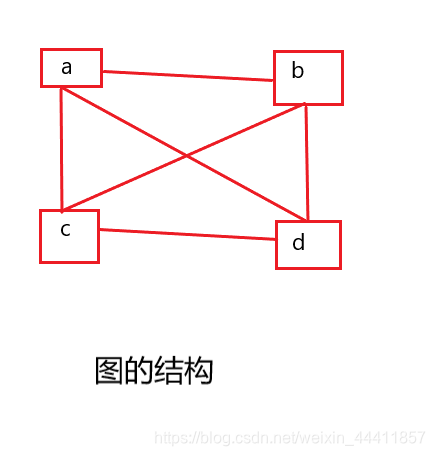
算法是想办法让计算机运行该程序的时候更节约时间和更节约硬盘占用，也就是让用户在老旧设备上操作体验和先进设备的体验是趋近的，不卡顿、人机交互友好，让用户觉得设备还能在战5年。其中一个重要概念是算法复杂度，分时间复杂度和空间复杂度。做复杂度分析的时候不考虑测试环境变化的影响，如我们不能指定用户运行我们程序的时候必须使用指定设备，所以复杂度分析要把客观因素抛开，即只看代码的运行情况。
时间复杂度：就是把执行每行代码所需时间看作是固定的（time），执行完所有代码所需时间。我们把时间复杂度用大O复杂度表示法来分析

//伪代码
int a（int n）{
	int sum=0;
	for（int i=0;i<=n;i++）{
		sum+=i;
	}
	printf("sum="+sum);
}

分析上面伪代码可以看出第二行执行时间是time，第三和第四行执行时间是2n*time；代码的执行时间（T（n））与代码（f（n））成正比，即T（n）=O（f（n））。上述代码的复杂度就是：T（n）=（1+2n）time；time趋近于某个常量，在分析复杂度时，常量和系数我们一般可以忽略，所以上述代码的时间复杂度可以趋近于看作是T（n）=n；

//还是伪代码
int a(int n){
	int sum=0;
	for(int i=0;i<=6;i++){
		sum+=i;
	}
	
	int sum_1=0;
	for(int j=0;j<=n;j++){
		sum_1+=j;
	}
	
	int sum_2=1;
	while(sum_2<=n){
		sum_2*=2
	}
	printf(sum+sum_1+sum_2);
}

上述代码就比较多了，但是复杂度分析的步骤也一样的，变量的声明是3time属于常量；第一个for循环也是常量27time；第二个循环是2ntime；while的时间复杂度是log2ntime（2是底数）；如果把代码sum_2*=2改为sum_2*=3,复杂度就是log3n*time（3是底数）；所以在探究复杂度的时候可以把底数去掉就是logn，综上所述，代码复杂度T（n）=（3+14+2n+logn）*time，通过计算得到复杂度是n。

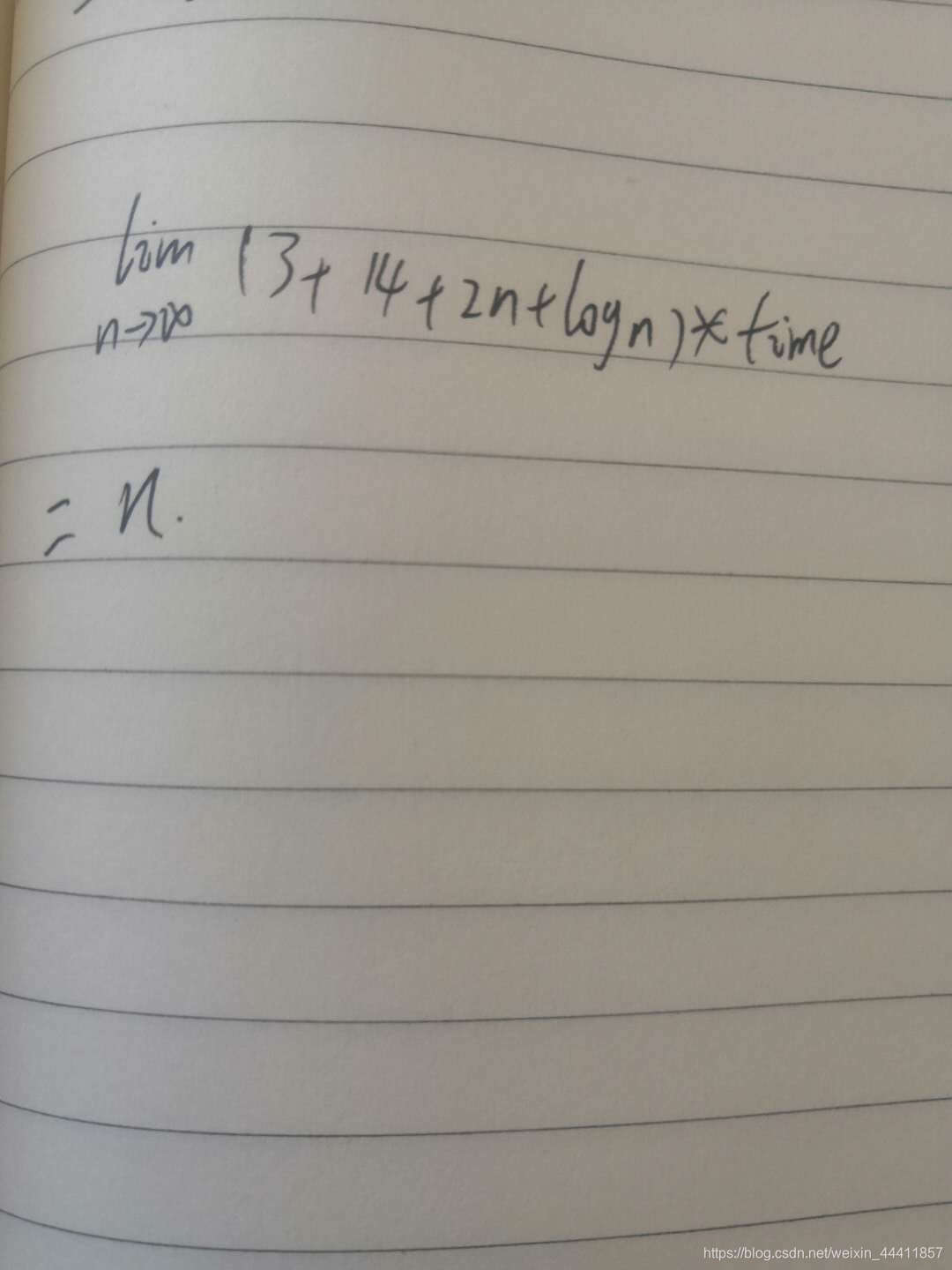
可以看出在代码里面我们只需要算出复杂度最高的代码块就可以了，一下列出几种常见的复杂度

空间复杂度分析于时间复杂度类似

//这是一个会被打死的伪代码
int a(int n){
	int sum=0;
	for(int i=0;i<n;i++){
		int b=1;
		sum+=b;
	}
	printf("sum="+sum);
}

上述代码sum申请一个空间，for循环里b申请了n个空间，所以空间复杂度就是n。写递归函数的时候就要特别注意空间复杂度的分析。
以上是复杂度的简单分析，在具体代码中还会涉及到最好情况复杂度、最坏情况复杂度、平均复杂度、均摊复杂度的分析

//伪代码
int d(int n){
	int[] a={1,2,3,4,6,8,5,7,9}
	for(int i=0;i<9;i++){
		if(a[i]=n){
			i=i+1;
			printf("该数在第"+i+"个");
			break;
		}
	}
}

第一种情况，n=1，for循环执行一遍就找到了,时间复杂度是1，这是最好时间复杂度；第二种情况，n=9，for循环执行n遍，时间复杂度就是n，这是最坏时间复杂度；更多的时候我们查找的数是在数组中间，这就涉及到平均复杂度和均摊复杂度可以自行百度查阅。
最后本文写的比较啰嗦，请各位读者海涵，有问题或者建议的可以在评论区指出，谢谢。