一起学算法系列之告别动态规划（一）

一起学算法系列之告别动态规划（一）

作者 : 玉龙小怪兽

前进的路伴随着成长。坚持，沉淀 , 分享 , 让自己和他人都有所收获

一、前言

不得不说几乎是程序员都知道或者了解数据结构与算法，大家都想掌握数据结构算法，尤其是同学想去比较好的厂， 奈何因为某些原因就没有继续学习它。比如，平时的业务开发用不到，没有坚持去下。似乎它就成了一座想越过却无法越过的大山。有必要去花很多的时间深入学习它吗 ？答案是肯定的，非常有必要。程序 = 数据结构 + 算法， 或许你现在从事的工作只需要简单的集合操作就可以完全90%的功能，请记住，这只是现在，不代表未来。

举个简单的例子， 如果有面值 1 ， 5 ， 10的硬币，请问现在要凑18元，218元，分别最少需要多少硬币？如果你没有了解动态规划算法 ，你会觉得该函数是真的不好写。拥抱数据结构与算法， 不单单是我刷了多少题（记住了多少题），而是用心真正的去理解它。只有这样， 我们才能站在算法的基础上，构建出更加优秀的代码。

二、动态规划的基础知识

动态规划:通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法 ,常适用于有重叠子问题和最优子结构性质的问题

动态规划的思想:大致上，若要解一个给定问题，我们需要拆解成若干个子问题并保存子问题的结果，再根据子问题的解推导出原问题的解.简单来说 ,就是当前的状态能通过上一个状态推导出来。

动态规划的核心解题步骤：

​ 1.确定并定义dp[i]代表的含义

​ 2.推导dp[i]的状态转移公式，确定上一个状态dp[i - 1] （不一定）与当前的状态dp[i]的关系

​ 3.初始化状态方程的值，根据dp[i]的状态转移公式，来确定需要初始化的值，从而根据初始化的值推 导出dp[i]的值，详细见下文

​ 4.根据初始化的值来确定遍历的开始与顺序

基本上每一道动态规划都会遵循以上的核心步骤 ， 核心的难点就在于如何确定状态方程，因为不同的题目， 状态方程是不同的。

下面 ， 就让我们通过练习一步一步的告别动态规划。

三、斐波那契数理解递推公式

题目：509. 斐波那契数

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1

F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给你 n ，请计算 F(n) 。

思路分析：

题目给出了斐波那契数的函数等式 f(n) = f(n - 1) + f(n - 2) ，其实这正是dp[i]的状态转移方程

牢记动态规划的解题步骤（重点）：

1.确定dp[i]的含义：

​ dp[i]表示：数值为i的斐波那契数的值为 dp[i]

2.dp[i]的状态转移方程

​ dp[i] = dp[i - 1] + dp[i - 2];

3.初始化值

​ 因为 dp[i - 1] 与 dp[i - 2] ， 可以确定 i >= 2开始 ,dp[i]才是有意义的，那么初始化呢?

​ dp[2 - 1] = dp[1] ：需要初始化

​ dp[2 - 2] = dp[0] : 需要初始化

所以需要初始化的是 dp[1] 和 dp[0] , dp[0] = 0 dp[1] = 1

4.完整代码

public int fib(int n) {
    if (n <= 1) return n;
    //定义dp[i]
    int[] dp = new int[n + 1];
    //初始化
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i -1] + dp[i -2];
    }
    return dp[n];
}

四、不同的路径理解如何初始化

题目：62. 不同路径

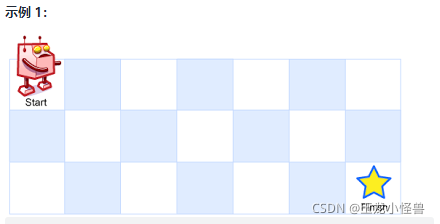
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

解题思路：

牢记动态规划的解题步骤（重点）：

1.确定dp的含义：

​ dp(i)(j)的含义表示：从（0,0）移动到(i，j)一共有dp(i)(j)种走法

2.dp(i)(j)的状态转移方程

​ 因为只能向右和向下走，所以dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1)，也就是只能通过上面一格或者左边一格到达指定位置。

3.初始化值

​ 因为dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1);所以当i >=1 , j >=1时，状态转移方程才有意义

所以初始化 dp(0)(j) 和 dp(i)(0) ，题目规定只能向下和向右移动，那么 dp(0)(j) 的走法只有1种 所以 dp(0)(j) = 1 ；同理 dp(i)(0) = 1；

4.完整代码

class Solution {
    public int uniquePaths(int m, int n) {
        //dp[i][j]: 到达网格 i j 时 , 共有 dp[i][j]种走法
        //dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        //初始化 dp[0][j]  dp[i][0] 
        int[][] dp = new int[m][n];
        //初始化数据
        for(int i = 0; i < m  ; i ++) {
            dp[i][0] = 1;
        }
        for(int i = 0; i < n ; i ++) {
            dp[0][i] = 1;
        }
        for(int i = 1; i < m  ; i ++) {
            for(int j = 1; j < n  ; j ++) {
                dp[i][j] = dp[i -1][j] + dp[i][j -1];
            }
        }
        return dp[m -1][n -1];
    }
}

五、总结

• 虽然只是两道非常基础的动态规划题 ， 但正是因为基础， 才把动态规划的思想体现出来，dp[i]如何去定义，dp[i]的初始化如何推导 ， 遍历的顺序如何求解。在做题的过程中，加入我们自己的思考，产生一些思想的碰撞，对也好，错也好，自己体味那种感觉是最好的，否则是很难坚持学习完整套数据结构与算法的。
• 本篇文章只是开始，下一篇继续带来动态规划的题解，一步一步告别动态规划。路很长，一起学好数据结构与算法 ，共勉！
• 文章基于个人的理解以及参考优秀的书籍，文章，如有错误，敬请指出！