人工智能作业 - A*算法程序求解八数码

A*算法

简介

A*搜寻算法俗称A星算法。A*算法是比较流行的启发式搜索算法之一，被广泛应用于路径优化领域。它的独特之处是检查最短路径中每个可能的节点时引入了全局信息，对当前节点距终点的距离做出估计，并作为评价该节点处于最短路线上的可能性的量度。

思路

A*算法通过函数 f(n) = g(n)+h(n) 来计算每个节点的优先级。
f(n)是节点n的综合优先级。
g(n) 是节点n距离起点的代价。
h(n)是节点n距离终点的预计代价，这也就是A算法的启发函数。关于启发函数我们在下面详细讲解。
A算法在运算过程中，每次从优先队列中选取f(n)值最小（优先级最高）的节点作为下一个待遍历的节点。另外，A*算法使用两个集合来表示待遍历的节点open_set，与已经遍历过的节点close_set。

A*伪代码

初始化open_set和close_set；
将起点加入open_set中，并设置优先级为0（优先级最高）；
如果open_set不为空，则从open_set中选取优先级最高的节点n：
    如果节点n为终点，则：
        从终点开始逐步追踪parent节点，一直达到起点；
        返回找到的结果路径，算法结束；
    如果节点n不是终点，则：
        将节点n从open_set中删除，并加入close_set中；
        遍历节点n所有的邻近节点：
            如果邻近节点m在close_set中，则：
                跳过，选取下一个邻近节点
            如果邻近节点m也不在open_set中，则：
                设置节点m的parent为节点n
                计算节点m的优先级
                将节点m加入open_set中

八数码问题

题目描述

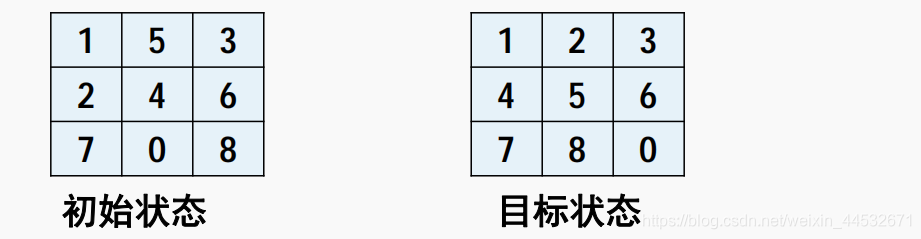
➢在一个３×３的九宫中有1-8这８个数字以及一个空格随机摆放在其中的格子里。将该九宫格调整到目标状态。
➢规则：每次只能将与空格（上、下、左、右）相邻的一个数字移动到空格中。试编程实现这一问题的求解。
➢备注：为了程序中表示方便，用0代替空格。
➢初始状态和目标状态：均由用户通过键盘手工输入或者从文件读入（不可以写死在程序里面）。
➢实验结果需要包含以下初始状态和目标状态的结果（check your answer:至少需要移动15步）。

注意事项

➢每个节点n需要记录父节点信息以及g(n)的值（已走过的步数）。
➢从当前状态到目标状态的代价估计h(n)可以从下面选一个（或者自拟）
h1(n):与目标相比, 错位的数字数目;
h2(n):曼哈顿距离总和（ D(i,j)=|X1-X2|+|Y1-Y2| ）;
若是能对两种代价函数进行实验比较（同一初始状态下，两种代价函数导致的搜索步数的差异，需对多个初始状态进行实验），则更好。
➢每个状态的子状态最多四个（上、下、左、右移动），但要根据空格所处的实际位置确定当前状态具体有哪几个子状态。

实验过程

解决思路

伪代码

输入数据

先检查是否一定有解。

直接A*算法求解。

输出结果

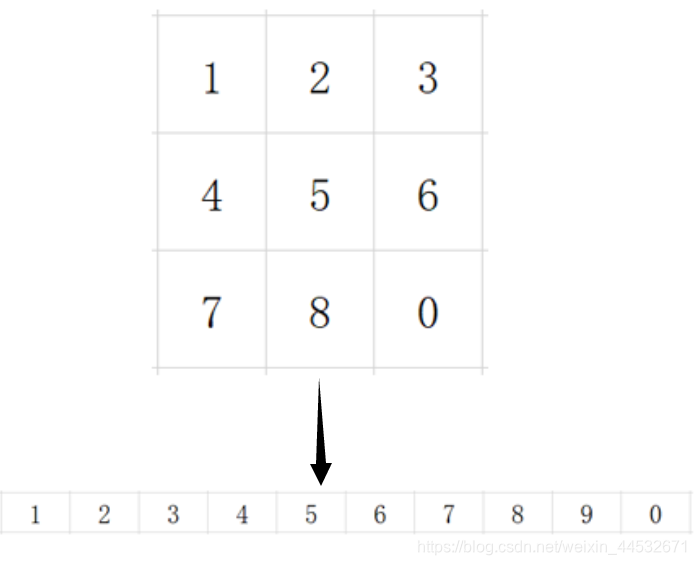
二维压缩为一维

需要注意的是，要把二维数组直接推平记录到字符串中，这样一来容易检查是否有解，而且更方便用open_set和close_set记录状态。
这样的话0号在二维数组中上下左右移动 就转换为 字符串中 与往前第三个字符互换位置，往0后第三个字符互换位置，相邻的互换位置

检查是否有解

若两个状态的逆序数奇偶性相同，则可相互到达，否则不可相互到达。
逆序数概念：

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。也就是说，对于n个不同的元素，先规定各元素之间有一个标准次序（例如n个 不同的自然数，可规定从小到大为标准次序），于是在这n个元素的任一排列中，当某两个元素的实际先后次序与标准次序不同时，就说有1个逆序。一个排列中所有逆序总数叫做这个排列的逆序数。

其他

set的使用
set里面会自动排序（从小到大）。重载结构体的小于号后，直接获取set第一个值就是当下优先级最高的。
记录路径的方法
没想到比较好的记录路径的方法，索性直接把路径存在每个状态结构体中。0上，1下，2左，3右

代码实现

#include<iostream>
#include<string>
#include<set>
#include<stack>
#include<map>
using namespace std; 
bool check(string tem) {
   
   
	//目标状态的逆序数是0，所以如果该状态的逆序对是奇数，无解，返回1；
	string  s = "";
	int cnt = 0;
	for (auto i : tem) {
   
   
		if (i != '0')
			s += i;
	} 
	int len = s.size();
	for (int i = 1; i < len; i++) {
   
   
		for (int j = 0; j < i; j++) {
   
   
			if (s[i] < s