【R语言】回归分析案例：北京市商品房价格影响因素分析

这一案例是王汉生老师《应用商务统计分析》方差分析章节的案例，主要对离散型变量进行了处理。
这里将连续型变量也加进来，进行协方差分析，建立完整的模型。

首先对房价进行对数变换，解决异方差问题：
进行描述性统计分析，各连续型变量之间的相关关系如下：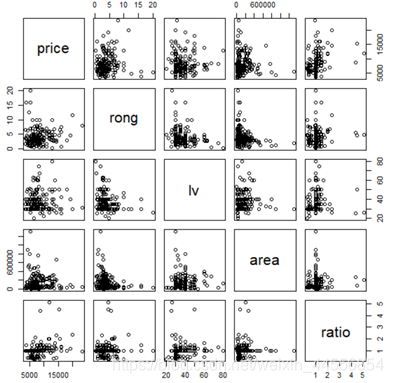
名义变量的EDA一般做箱型图。

模型按照全模型-变量处理（分箱等）-变量选择-回归诊断等步骤建立。

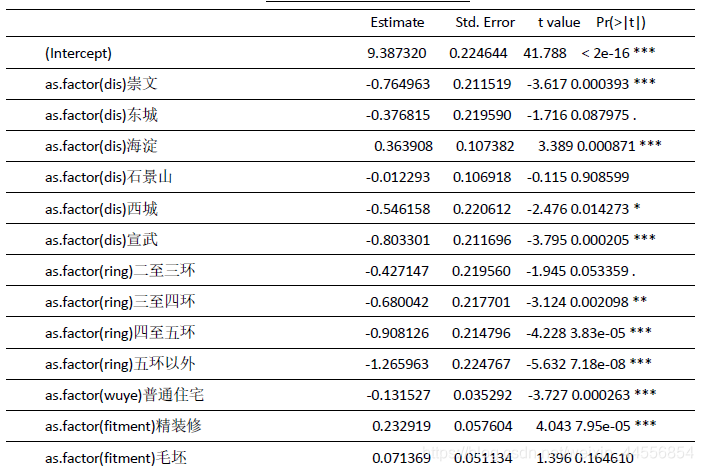
最终模型残差图：

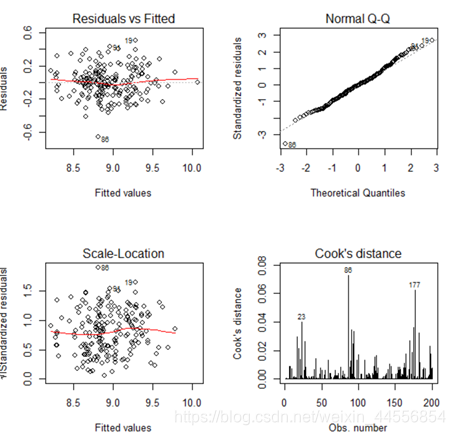
通过模型分析结果可知，影响北京市商品房平均销售价格的主要因素有：
属性变量：所在辖区、所在环线、物业类别、装修状况、容积率大小（新引入）；连续变量：绿化率、停车位住户比
属性变量的具体影响在此处分析略去。
连续型变量的影响主要为：
 绿化率：绿化率的影响十分显著，由系数估计值为正，说明对房价有正向影响，绿化率越高的楼盘房价越高；
 停车位住户比：有较显著的影响，停车位住户比越高，价格越高；
同时，原本为连续型变量的容积率经过离散化变为属性变量后：
 容积率大小：容积率分组有较显著的影响，高容积率的小区商品房价格更贵；
 容积率与环线之间存在着交互效应。

rm(list=ls())										#清空当前工作空间
setwd("D:/回归分析")
a=read.csv("real.csv",header=T)		#读入csv格式的数据，赋值为a
View(a)
attach(a)
names(a)

##描述性统计

#未做处理的响应变量分布情况
par(mfrow=c(1,1))
hist(price)
summary(price)        #查看响应变量的描述统计量
#连续型变量描述性统计
windows()
pairs(a[,c(6:10)])    #所有连续型变量间的散点图
par(mfrow=c(2,2))	
plot(rong,price)      #每个连续型因变量与响应变量间的散点图
plot(lv,price)
plot(area,price)
plot(ratio,price)
summary(a[,c(6:10)])  #查看连续型变量的描述统计量
cor(a[,c(6:10)])      #查看连续型变量的相关系数
#属性变量描述性统计
windows()
par(mfrow=c