论文阅读 (85)：Residual Attention-Aided U-Net GAN and Multi-Instance Multilabel Classifier for Automatic

0 概述

0.1 题目

2022：用于重叠LPI雷达信号自动波形识别的残差注意力U-Net GAN和多示例多标签分类器 (Residual attention-aided U-Net GAN and multi-instance multi-label classifier for automatic waveform recognition of overlapping LPI radar signals)

0.2 摘要

低拦截概率 (Low probability of intercept, LPI) 雷达信号自动波形识别 (Automatic waveform recognition) 是电子侦察领域的一项重要任务，随着频谱环境的复杂化，其所面临的挑战也日益增长。本文提出了一个重叠LPI波形识别处理框架，其整合了残差注意力U-Net对抗生成网络 (Generative adversarial network, GAN)。该框架包含五个模块，在训练集仅仅是单类型信号的情况下，也能获得很好的识别性能：

1. 训练信号被转换为时频图；
2. 使用具有残差学习的残差注意力U-Net GAN (RAUGAN) ，以噪声图像作为输入，并在高质量图像的监督下重建信号图像；
3. 具有非对称卷积的实例生成模型生成实例表示，该结果作为后续的残差注意力MIML分类器 (RAMIML) 的输入；
4. 自适应阈值校准模块生成合适的阈值，以获取最终决策；
5. RAUGAN和RAMIML分别在自己的损失函数下优化。

0.3 引用

@article{Pan:2022:43774395,
author		=	{Ze Si Pan and Sha Fei Wang and Yun Jie Li},
title		=	{Residual attention-aided {U-Net} {GAN} and multi-instance multilabel classifier for automatic waveform recognition of overlapping {LPI} radar signals},
journal		=	{{IEEE} Transactions on Aerospace and Electronic Systems},
pages		=	{4377--4395},
year		=	{2022},
volume		=	{58},
number		=	{5},
doi			=	{10.1109/TAES.2022.3160978}
}

1 引入

低拦截概率 (Low probability of intercept, LPI) 雷达广泛应用于LPI雷达和雷达嵌入式通信等领域，其目标是防止敌对接收器拦截，以及感知传输信号。实际的电磁环境中存在大量的LPI发射器，由电子侦察系统拦截的多个信号可能在时域和频域上重叠。由此衍生了名为重叠LPI波形识别 (Overlapping LPI waveform recognition, OLWR) 的特定自动调制识别 (Automatic modulation recognition, AMR) 任务。

特征提取和分类是AMR相关任务中不可或缺的两个部分。特征提取的目的是实现数据降维，并获取具有辨别特性的高效特征表征。强分类器的准则是使用合适算法构建超平面，以区分候选类别。因此，为了改进OLWR任务的处理框架，应当重点关注以上两个部分。

信号的质量是特征提取部分的一个关键，由于低信噪比 (Signal-to-noise ratio, SNR) 环境的存在，前景信号将被模糊并被噪声覆盖。相当数量的研究人员研究了这个问题，其中降噪和信号重构是消除噪声影响以及保护前景信号特征的两个常用方法。这些工作中，例如奇异值分解、经验模式分解，以及小波变换等，通常使用信号不同领域中的子空间算法和先验信息，迭代地将确定信信号与噪声区分开。这些方法能够很大程度上提升信号的质量。然而，它们可能丢失感知质量的细节并遭受伪影的困扰。此外，弱扩展性是它们在实际应用中的另一个潜在风险。

深度学习 (DL) 方面衍生了很多新颖的信号重建算法。对抗生成网络 (GAN) 也被广泛研究，其基本准则在于两个共存网络之间的对抗：生成器使用随机噪声作为输入，并在鉴别器的监督下输出合成样本。Goodfellow首次引入GAN，其学习训练数据的基本分布，以生成难以区别于输入数据的新的真实数据样本。事实上，GAN是用于图像重构的前沿算法，获取了前所未有的真是图像。在超分辨率领域，Ledig等人通过结合对抗损失与内容损失，提出了超分辨率GAN (SRGAN)。尽管残差学习被用于缓解梯度问题，该方法依然存在生成能力的不稳定性问题。基于U-net的方法被提出用于提升表征能力，并广泛应用于语义分割以及目标检测。此外，U-net也被引入到了图像传输。pix2pix框架提供了一个关于有监督image-to-image传输问题的通用解决方案，其核心便在于使用U-net结构替换了生成器。Armanious等人应用U-net将low-dose CT图转译到high-dose CT图。而在我们的知识范围内，鲜有用于雷达信号重构的GAN方法。

多分类学习 (MCL)、多标签学习 (MLL)、多示例学习 (MIL)，以及多示例多标签学习 (MIML) 是用于OLWR分类器设计的常用算法。MCL是MLL和MIL的退化版本，其在处理信号分类时仅有一个标签。因此，OLWR的泛化不可避免地使其难以求解：

1. MCL方法将重叠信号视作一种新类型，而标签集的数量随着候选标签数量的增长呈指数级变换；
2. MLL方法能够标记每一个分量信号，并将相应的标签分配到输出向量。然而，其将重叠信号视作单独的一个实例，这将忽略不同内容的语义信息；
3. MIL引入包学习的概念，其聚焦局部语义信息，从实例级别到包级别进行细粒度预测。MIL主要的局限是，当处理重叠信号时，其仅会被标记为单独的一个分量。

MIML结合了这些方法的优势，在其理论中，一个图像表示为关于实例的包并于多个标签关联。MIML的目标是寻找局部区域与标签的关系，以分类无标记图像。Feng等人提出了以卷积神经网络 (CNN) 为基底的DeepMIML网络。Song等人则引入了多模态CNN，提出了MMCNN-MIML，其利用了标签之间的相关性，并将组的文本上下文与视觉实例结合，以辅助分类。

早期的重叠信号识别通常使用统计特征，但是其通用性和抗干扰性远远达不到要求。如今，基于DL的结构普遍用于提取特征。Liu等人提出了一个反复选择策略，其通过重复利用CNN来分割时频图和分类所选区域。Si和Qu等人均将CNN作为基础架构，并分别使用sigmoid函数和深度Q-learning网络来辅助MLL分类器。Ren等人利用注意力ResNeXt，并将每个重叠信号看作是一个新类来结合重叠信号的多领域特征，包括时间、频率、自相关，以及时频域。MIML-DCNN首次在OLWR中引入MIML，其可以在SNR为-6dB取得83%的总体性能。该框架使用VGG16作为骨架，以提取特征，并使用深度MIML分类器来预测分量类型。表1从不同角度比较了这些用于OLWR任务的主流方法。为了提升MIML方法的性能，可以从以下两个角度出发：

1. 生成去噪模型，例如GAN用于实现低SNR下的波形识别；
2. 注意力机制和残差结构辅助的特征表征与分类模块可以使模型关注突出区域，并捕捉重要的内容信息。

本文提出了一个用于OLWR任务的波形识别框架RAUnetGAN-MIML：

1. 利用平滑伪Wingner-Ville分布 (SPWVD) 将截获到的重叠信号转换为时频图 (TFI)；
2. 非对称卷积实例生成模块生成多种类型的实例；
3. 残差注意力MIML (RAMIML) 结合自适应阈值校准模块实现分类。

本文的主要贡献如下：

1. 提出了一个用于OLWR任务的RAUnetGAN-MIML框架。注意力机制同时引入到了RAUGAN和RAMIML分类器中。显著的表征能力与多样化实例表征结果，以提升识别性能；
2. 基于MIML原理，分类器基于单类型信号训练，可以在低SNR情况下获取不错的结果；
3. 设计了新颖的损失函数，集RAUGAN的损失函数中集合了均值绝对误差 (MAE) 和均方误差 (MSE)，而RAMIML的损失函数中集合了交叉熵和lasso正则。该损失函数可以捕捉高频内容，并辅助稀疏MIML问题的求解。

2 信号模型和OLWR任务说明

2.1 信号模型

假设电子环境中有几个独立的发射器，所有的发射器将在相似的载波频率下传输信号。因此，被动侦察系统截获的信号可能在时域和频域上重叠。考虑到截获的重叠信号受到加性高斯白噪声 (Additive white Gaussian noise, AWGN) 的干扰，重叠信号的接受复包络的一般表达为：
$$\begin{array}{rl}{y}_{\text{overlaping}}& =\sum _{i=1}^K{S}_i(nT)+\omega (nT)\\ & =\sum _{i=1}^K{h}_i{A}_i{e}^{j(2\pi \Delta f_i(nT)+{\varphi }_i+{\theta }_i)}+\omega (nT),\end{array}\text{\hspace{1em}(1)}$$其中$T$表示采样间隔、$S_i(nT)$是来自第$i$个发射器的离散时间复信号，以及$\omega (nT)$表示具有零均值和方差${\delta }^2$的复AWGN。此外，$h_i$表示来自第$i$个发射机的信道系数、$A_i$是非零常数信号包络、$\Delta f_i(nT)$表示载波频率，${\varphi }_i$和${\theta }_i$则分别表示第$i$个发射器和接受天线之间的相位抖动和相位偏移。表2展示了本文的常用符号。

本文将研究SNR和功率比 (PR) 的影响，其定义如下：
$$\text{SNR[dB]}=10{\log }_{10}\frac{{\sum }_{i=1}^K|h_i{A}_i{|}^2}{{\delta }^2}.\text{\hspace{1em}(2)}$$$$\text{PR(dB)}=20{\log }_{10}\frac{A_i}{A_n}.\text{\hspace{1em}(3)}$$此外，在复杂的电磁环境中，每个发射器以相互独立的方式发射信号。因此，由来自每个发射源的信号组成的新重叠信号的模式是随机的。在这种情况下，重新信号的组合数量指数于标签的数量：
$$N_{\text{overlapping}}=\sum _{q=1}^K{C}_K^q,\text{\hspace{1em}(4)}$$其中$C_K^q$表示$K$中的$q$个组合，以及$q$表示分量信号类型的数量。

2.2 OLWR在MIML上的定义

在实际应用中，多语义对象通常标记有多个标签，且能够被表示为多个虚拟表征，这被看作是多个实例组成的包。例如，景观分类中的每个图像可能有多个作为实例的区域，依次被分配为海洋或者沙滩等标签，这些标签同样反馈在图像级别上。

这种关于复杂对象的结构可以应用到OLWR任务上。令$S$表示实例空间，$W$表示类标签集合。训练集 { S j , W j } j = 1 J \{S^j,W^j\}_{j=1}^J {Sj,Wj}j=1J​包含$J$个包，每个包$S^j$包含$h$个实例 { I 1 j , I 2 j , … , I h j } \{I_1^j,I_2^j,\dots,I_h^j\} {I1j​,I2j​,…,Ihj​}。$W_j$是候选标签 { w 1 j , w 2 j , … , w l j } \{w_1^j,w_2^j,\dots,w_l^j\} {w1j​,w2j​,…,wlj​}的集合，与$S^j$关联，其中$l$是候选单标签$W^j$的数量。当S^j被分配到第$l$个标签时，$w_l^j=1$，否则为$-1$。所需的目标函数为$f_{\text{MIML}}:2^S\to 2^W$，其输出一个标签向量，有 f MIML ( S ) ∈ { 0 , 1 } l f_\text{MIML}(S)\in\{0,1\}^l fMIML​(S)∈{0,1}l。

3 方法

3.1 OLWR框架

图1展示了RAUnetGAN-MIML的流程图。训练过程分为五个步骤：

1. 通过时频分析 (TFA) 获取TFI；
2. RAUGAN进行高质量图像重构；
3. ResNet34生成多样化实例表征；
4. RAMIML用于脉冲内调制识别；
5. 阈值校准和标签预测。
   

3.2 TFA

TFA是特征提取的一个预处理步骤，其将截获的信号转换为TFI，用于后继分类的使用。Winger-Vile分布 (WVD) 是常用的TFA方法，其利用自相关来获得抗噪声和高时频分辨率的健壮性：
$${\text{WVD}}_x(t,f)={\int }_{-\infty }^{+\infty }y(t+\frac{\tau }{2})y^{\ast }(t-\frac{\tau }{2})e^{j2\pi f\tau }d\tau ,\text{\hspace{1em}(5)}$$其中$t$是时间戳、$f$是角频率，$\tau$是时滞。噪声重叠信号$y(t)=x(t)+n(t)$的的WVD表示为：
WVD y ( t , f ) = WVD x + n ( t , f ) = WVD x + WVD n + 2 R e { WVD x n } , (6) \tag{6} \begin{aligned} \text{WVD}_y(t,f)=&\text{WVD}_{x+n}(t,f)\\ =&\text{WVD}_x+\text{WVD}_n+2Re\{\text{WVD}_{xn}\}, \end{aligned} WVDy​(t,f)==​WVDx+n​(t,f)WVDx​+WVDn​+2Re{WVDxn​},​(6)其中${\text{WVD}}_x$和${\text{WVD}}_n$分别表示纯净信号和附加噪声的自相关项。 2 R e { WVD x n } 2Re\{\text{WVD}_{xn}\} 2Re{WVDxn​}表示可能干扰WVD图像质量并隐藏LPI雷达波形特性的二次交叉项。

SPWVD用于缓解WVD中交叉项的影响，其广泛应用于Cohen类别转换。SPWVD转换定义为：
$${\text{SPWVD}}_x(t,f)={\int }_{-\infty }^{+\infty }h(\tau ){\int }_{-\infty }^{+\infty }g(s-t)\cdot x(s+\frac{\tau }{2})x^{\ast }(s-\frac{\tau }{2})e^{j2\pi f\tau }dsd\tau ,\text{\hspace{1em}(7)}$$其中$g(s-t)$和$h(\tau )$分别是时域和频域上的窗口函数。

得益于时域和频域上的平滑分布，SPWVD可以通过调制窗函数的长度来抑制交叉项干扰，并在每个分量的瞬时频率保持自动项抑制。随后，为了应对后继处理，每一个TFI被调整大小为$256\times 256\times 3$，其中$256$表示高和宽，$3$表示通道数。

3.3 残差注意力U-net GAN

GAN提供了一个生成看似合理的的高感知质量图像的方法。具有高概率包含真实图像的区域通过GAN从搜索空间的区域重构，因此生成的图像很接近于原始图像。我们使用高SNR (高分辨率, HS) 的有监督TFI作为输入，并使用U-net作为生成器，以重构低SNR (低分辨率, LS) TFI。这个过程通常可以描述为共享相似结构但外观不同的两个域之间的回归任务。在加性高斯白噪声AWGN的作用下，$I^{\text{LS}}$是HS版本$I^{\text{HS}}$的LS版本。注意$I^{\text{HS}}$仅在训练阶段可用。

对抗生成网络的目标函数使用min-max优化等式解释：
$$\underset{G}{\min }\underset{D}{\max }{L}_{\text{GAN}},\text{\hspace{1em}(8)}$$其中$L_{\text{GAN}}$是对抗损失：
$$L_{\text{GAN}}={\mathbb{E}}_{I^{\text{HS}}\sim P_{\text{train}}(I^{\text{HS}})}[\log D(I^{\text{HS}})]+{\mathbb{E}}_{I^{\text{LS}}\sim P_{\text{train}}(I^{\text{LS}})}[\log (1-D(G(I^{\text{HS}})))].\text{\hspace{1em}(9)}$$对立网络的目标函数是依赖的，收敛则通过Nash均衡来实现。公式的核心点是生成器$G$通过模拟输入数据来愚弄鉴别器$D$，而$D$需要识别真实或者人造图像。在这种情况下，训练好的$G$能够习得接近真实的图像，$D$将难以判断。

在RAUGAN中，最终的目标是训练一个生成函数，其通过评估HS图像来输出LS图像。图2展示了$G$的结构。

为了从生成样本中辨别出真实HS TFI，我们训练了一个鉴别器网络：

1. 在通道维拼接LS和HS TFI；
2. 五个连续的卷积核大小为$3\times 3$的卷积被使用。除第一层外，每个后接leaky ReLU和批量归一化；
3. 输出的特征图传递给两个稠密层和一个sigmoid函数，以为高置信度图像分配接近1的输出值。

因此，鉴别器可以判断TFI是否是HS。

在噪声和干扰的作用下，卷积CNN可能不能关注到特征图中的有效区域。对此，跳跃连接和注意力机制被用于U-net结构，以辅助其捕获特征图中的突出信息及抑制不相关背景特征。跳跃连接可以拼接高阶和低级特征，这有利于补充更确切的局部信息。注意力机制用于捕捉高级别语义信息并突出特征，亦可以缓解无用背景信息的干预。特别地，RAUGAN提取低级别特征的局部信息和高级别特征的全局信息，因为深层的感受野更大。深层作为浅层的注意力查询来学习其分布，这可以引导浅层特征图选择重要的位置细节并保留与前景目标相关的激活区域。

注意力机制如图2，首先获得深层特征图上与浅层特征图相同大小的采用，然后进行按元素拼接以进行特征融合。通过激活函数后，通过按元素乘法和注意力权重调整获得输出。注意力机制可以制定为：
$$W_a={\eta }_2(\phi (({\eta }_1(x^d+x^s))+b_{\phi })),\text{\hspace{1em}(10)}$$其中$W_a$是注意力系数，${\eta }_1$和${\eta }_2$分别是ReLU和sigmoid函数。对于输入特征图，线性变换$\phi$使用$1$-$1$过滤核的卷积层来计算，其中$b_{\phi }$表示偏差。$x^d$和$x^s$表示深层和浅层特征图。

为了生成真假结合的图像，损失函数是很重要的。单独使用对抗损失，并不能很好地重构LS图像。特别地，TFI通常只占据图像中的一小部分。通过计算像素值，目标信息大约只有$10$-$15\%$，这意味着整个图像中的感兴趣区域 (ROI) 是相当稀疏的。此外，与所需的真实图像不同，由于TFI的稀疏性和语义相关性不同于常见的风景图像，输出的图像可能改变全局特征。按像素重构损失用于缓解这个问题。按像素MSE损失定义如下：
$$l_{\text{MSE}}=\frac{1}{H_i{W}_i{D}_i}\sum _{x=1}^{H_i}\sum _{y=1}^{W_i}{\left({\phi }_i\left(I_{x,y}^{HS}\right)-{\phi }_i\left(G\left(I_{x,y}^{LS}\right)\right)\right)}^2,\text{\hspace{1em}(11)}$$其中$H_i$、$W_i$，以及$D_i$分别表示第$i$个卷积快上特征的高、宽，以及深度。${\phi }_i$表示中间层的输出。

尽管如此，这些种类的损失可能会导致模糊的结果，表明全局结构是以丢失细节和造成扭曲为代价的。已有方法已经证明结合额外的损失到目标函数是一种高效的途径。因此，一个固定的内容损失 (Content loss) 被用于捕捉高频内容，其也将保留图像的高峰值信噪比 (PSNR)。内容损失结合了MAE，能够惩罚不同频率分量表征的差异。MAE用于确保合成图像与信号图像的稀疏一致性。$I^{HS}$和KaTeX parse error: Expected 'EOF', got '&' at position 2: I&̲{LS}之间的内容损失表示为：
$$l_{\text{Content}}=\frac{1}{H_i{W}_i{D}_i}\sum _{x=1}^{H_i}\sum _{y=1}^{W_i}\Vert {\phi }_i\left(I_{x,y}^{HS}\right)-{\phi }_i\left(G\left(I_{x,y}^{LS}\right)\right){\Vert }_1.\text{\hspace{1em}(12)}$$因此，最终生成器的损失函数为：
$$\begin{array}{rl}{L}_{\text{gen}}=& l_{\text{MSE}}+l_{\text{Content}}\\ =& {\lambda }_1\frac{1}{H_i{W}_i{D}_i}\sum _{x=1}^{H_i}\sum _{y=1}^{W_i}{\left({\phi }_i\left(I_{x,y}^{HS}\right)-{\phi }_i\left(G\left(I_{x,y}^{LS}\right)\right)\right)}^2\\ +& {\lambda }_2\frac{1}{H_i{W}_i{D}_i}\sum _{x=1}^{H_i}\sum _{y=1}^{W_i}\Vert {\phi }_i\left(I_{x,y}^{HS}\right)-{\phi }_i\left(G\left(I_{x,y}^{LS}\right)\right){\Vert }_1,\end{array}\text{\hspace{1em}(13)}$$其中${\lambda }_1$和${\lambda }_2$是用于网络优化的非负调控参数。参数的选择将在本节末尾说明。

3.4 实例生成模块

本小节生成多样化的实例表征，其有用性已被已有方法证明。一般来说，CNN在多标签图像上的应用面临两大限制：

1. 雷达训练数据集的规模不足以支持训练一个端到端网络；
2. 标准CNN将输入特征作为一个整体，通常忽略多语义信息，且将其编码为一个1-D向量，这使得图像级别的多标签数据的识别很困难。

本文通过平行放置三个卷积核，设计了一个用于提升实例表征多样性的实例生成模块，其中过滤器的大小分别为$1\times 3,3\times 3,3\times 1$。非对称卷积丰富了特征空间并加强了方形卷积核的中心骨架部分。AlexNet、VGGNet、ResNet等常用于特征提取，其中ResNet能够避免随着网络深度的增加而出现的梯度消失和爆炸。因此，我们选择ResNet34作为深层特征提取的骨架，其最后三个卷积层及随后的池化层与全连接层被省略。具体来说，我们替换了后续卷积层中的非对称卷积滤波器，并用信号数据集更新参数。

对于输入特征图$I\in {\mathbb{R}}^{H\times W\times C}$，这里有三个卷积核$K_{\ast }|in{\mathbb{R}}^{U\times V\times C}$，其中$K_{\ast }$表示如之前所述的三个不同的卷积核。这样做是为了生成具有相同分辨率的输出。然后将三个卷积层的输出相加：
$$\begin{array}{rl}O& =O_{K_1}+O_{K_2}+O_{K_3}\\ & =I\times K_1+I\times K_2+I\times K_3,\end{array}\text{\hspace{1em}(14)}$$其中$I$是输入矩阵，$O_{K_1}$、$O_{K_2}$，以及$O_{K_3}$是不同卷积层的输出。一个批量归一化层用于避免过拟合，并加速收敛，因此，公式14可以重写为：
$$\begin{array}{rl}O& =O_{K_1}+O_{K_2}+O_{K_3}\\ & =\sum _{i=1}^3\left[(I\times K_i-{\mu }_i)\frac{{\gamma }_i}{{\sigma }_i}+{\beta }_i\right]\\ & =I\times \sum _{i=1}^3\left[\left(K_i\times \frac{{\eta }_i}{{\sigma }_i}\right)-\frac{{\mu }_i{\gamma }_i}{{\sigma }_i}+{\beta }_i\right]\\ & =I\times \sum _{i=1}^3\left(K_i\times \frac{{\gamma }_i}{{\sigma }_i}\right)+b,\\ b& =-\sum _{i=1}^3\left[\frac{{\mu }_i{\gamma }_i}{{\sigma }_i}+{\beta }_i\right],\end{array}\text{\hspace{1em}(15–16)}$$其中${\mu }_i$和${\sigma }_i$分别表示按通道的平均值和批量归一化的标准差。${\gamma }_i$和${\beta }_i$表示习得的规模因子和偏差项，其中$b$表示偏差项的计算和。

如图3所示，最终的实例表征3-D层是通过堆叠2-D实例表针所获得。每个实例的大小为$14\times 14\times 256$，其中$256$表示实例的数量，$14\times 14$表示$I_i^j$的形状。

3.5 残差注意力MIML分类器

本小节中，一个级联注意力架构被用作MIML分类器，其包含一个按通道注意力和一个按空间注意力。给定中间层特征图$F\in {\mathbb{R}}^{H\times W\times C}$作为输入，通道注意力图$M_c\in {\mathbb{R}}^{1\times 1\times C}$和空间注意力图$M_s\in {\mathbb{R}}^{H\times W\times 1}$如图4。

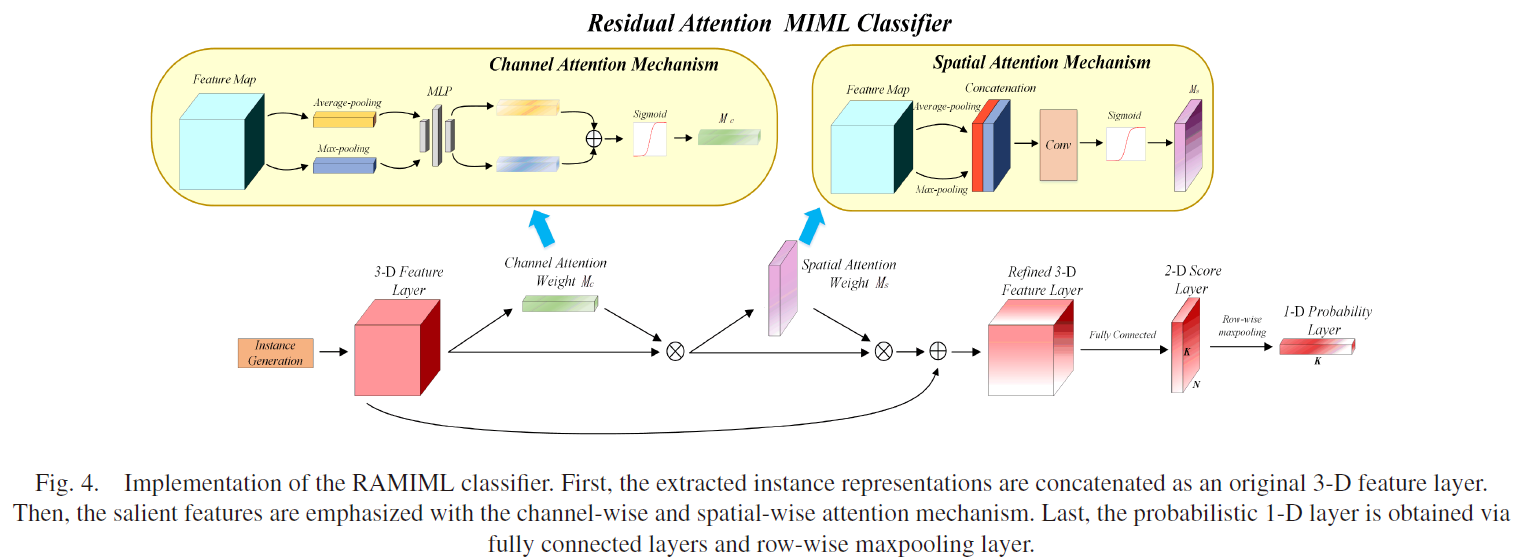
对于通道注意力，输入特征图在空间维度上聚合以生成通道权重描述器，并关注给定输入图像的重要部分。平均池化和最大池化用于捕捉不同的对象特征。

两个通道描述符被表示为$F_{\text{avg}}^c\in {\mathbb{R}}^{1\times 1\times C}$和$F_{\text{max}}^c\in {\mathbb{R}}^{1\times 1\times C}$，其分别表示平均池化和最大池化。然后，它们后面是一个简单的反向传播结构多层感知器。通过每个描述器之后，输出的特征向量在通过按元素求和合并为通道注意力图$M_c$。最后，残差模块被加入到通道注意力机制中。通道注意力模块的输出特征图表示为：
$$\begin{array}{rl}{O}_c& =(M_c(F)+1)\times F\\ & =[\zeta (\delta (Ave(F)+Max(F)))+1]\times F\\ & =[\zeta (\delta (F_{\text{avg}}^c+F_{\text{max}}^c))+1]\times F,\end{array}\text{\hspace{1em}(17)}$$其中$\delta$和$\zeta$分别表示ReLU和sigmoid。

与通道注意力不同，空间注意力关注ROI所在的特征图。相应地，通道维上使用了平均池化和最大池化，以生成两个2-D空间描述器$F_{\text{ave}}^s\in {\mathbb{R}}^{1\times H\times W}$和$F_{\text{max}}^s\in {\mathbb{R}}^{1\times H\times W}$。两个描述器拼接之后，一个卷积层用于获得空间注意力图$M_s$。最终，引入残差块后，空间注意力模块的输出特征图表示维：
$$\begin{array}{rl}{O}_s& =(M_s(F)+1)\times F\\ & =[\zeta (f^{5\times 5}([Ave(F);Max(F)]))+1]\times F\\ & =[\zeta (f^{5\times 5}([F_{\text{avg}}^s;F_{\text{max}}^s))+1]\times F,\end{array}\text{\hspace{1em}(18)}$$其中$\zeta$表示sigmoid，$f^{5\times 5}$表示卷积核大小为$5\times 5$的卷积层。

未来同时部署通道注意力和空间注意力，我们将这两个结构级联以获得相互补充的3-D特征：
$$\begin{array}{rl}{O}_{\text{overall}}=& (M_s(M_c(F)+1)\times F_{\text{in}}+1)\\ & [(M_c(F)+1)\times F_{\text{in}}]\end{array},\text{\hspace{1em}(19)}$$其中$F_{\text{in}}$表示网络的输入特征。

获取3-D特征之后，对于每个TFI，可以计算其包级别的标签。如图4，其将传递给全连接层，以获取大小为$N\times K$的2-D得分，其每个位置$(i,j)$表示表示第$i$个实例的第$j$个标签。接下来，按行最大池化层用于获取大小为$K\times 1$的1-D概率层，其长度等同于候选调制类型的数量。包级别预测通过最大匹配分数获得。为了将预测的输出缩放到$[0,1]$，sigmoid函数被使用，第$j$个标签计算为：
$$p(x_j)=\frac{1}{1+e^{-x_j}}(j\in 1,2,\dots ,K).\text{\hspace{1em}(20)}$$对于重叠信号，稀疏约束意味着期望信号区域接近或等于1，其余部分为0，相当于MIML原理。基于此，RAUnetGAN-MIML的损失定义为：
$$\begin{array}{rl}{L}_{\text{sparse }}=& -\sum _{i=1}^K{\alpha }_1[y_i^m\log \left(p_i^m\right)+\left(1-y_i^m\right)\log \left(1-p_i^m\right)\\ & +{\alpha }_2{\Vert p_i^m\Vert }_1]+\frac{{\alpha }_3}{2}\Vert \theta {\Vert }_2,\end{array}\text{\hspace{1em}(21)}$$其中$p_i^j$表示图像$S^j$关于第$i$个标签的输出向量，$y_i^j$表示$S^j$的真实标签。$\alpha$是非负权重参数、${\alpha }_2$是稀疏因子，以及${\alpha }_3$是正则参数。所有的参数都通过交叉验证获取。

3.6 自适应阈值校准模块

预测的输出向量$\mathbf{p}=[p_1,p_2,\dots ,p_K]$。然后，我们需要通过阈值校准获得预测标签 L = [ L 1 , L 2 , … , L K ] ∈ { 0 , 1 } K \boldsymbol{L}=[L_1,L_2,\dots,L_K]\in\{0,1\}^K L=[L1​,L2​,…,LK​]∈{0,1}K。在没有先验信息时，阈值通常设置为$0.5$，而在一些具体的领域，这需要根据实际情况而变化。为了输出重叠信号每个分量的预测概率，我们对不同的分量使用不同的阈值。这里引入平衡指示器F-measure，阈值$\sigma$被计算为：
$$\sigma =\mathrm{argmax}\frac{2{\sum }_{q=1}^K{\sum }_{j=1}^J{t}_{jq{T}_{jq}}}{{\sum }_{q=1}^K{\sum }_{j=1}^J{t}_{jq}+{\sum }_{q=1}^K{\sum }_{j=1}^J{T}_{jq}},\text{\hspace{1em}(22)}$$其中$\mathbf{t}=[t_{j1},t_{j2},\dots ,t_{jq}]$和 T = { T j 1 , T j 2 , … , T j q } \boldsymbol{T}=\{T_{j1},T_{j2},\dots,T_{jq}\} T={Tj1​,Tj2​,…,Tjq​}分别表示输出标签和真实标签。算法1描述了RAUnetGAN-MIML的完整训练过程。

4 实验设计

4.1 数据集描述

典型的LPI雷达信号包括线性调频、Barker编码、Frank编码，以及Costas编码。这些波形的详细参数如表3，其中$U(\cdot )$表示有理数的均匀分布。例如，设置频率$f=15$kHz，采用频率$f_s=150kHz$。标准化的频率表示为$U(\frac{f}{f_s})=U(\frac{1}{10})$。SNRf分别取-20和20dB，不同的单调制信号分别生成200个信号样本，以提供用于训练RAUGAN的LS和HS TFI。

随后，SRR从-20以2的步长变化到0dB的单信号和重叠类型信号用于生成TFI。对于每一个SNR值，生成了200个模拟信号样本。重构图像被调整为$224\times 224\times 3$，以适应ResNet34的输入。重构数据集被分为训练集和测试集，以评估识别性能。这衡量了当训练数据仅为单调制信号时的模型执行情况。因此，这里共考虑了11种类型的重写信号，测试集和验证集的比例为$4:1$，其中验证集用于确定阈值向量。

4.2 评价指标

PSNR和结构性相似度 (Structural similarity, SSIM) 被用于平局生成图像和基于GAN结构的性能。