单因素方差分析
问题:
消费者与产品生产者、销售者或服务提供者之间经常发生纠纷。发生纠纷后,消费者常常会向消费者协会投诉。为了对几个行业的服务质量进行评价,消费者协会在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业最为样本。其中零售业抽取了7家,旅游业抽取6家,航空公司抽取5家,家电制造业抽取5家。每个行业中所抽取的这些企业,假定它们在服务对象、服务内容、企业规模等方面基本上是相同的。然后统计出最近一年中消费者对着23家企业投诉的次数。结果数据如下。
一般而言,受到投诉的次数越多,说明服务的质量越差。消费者协会想知道这几个行业之间的服务质量是否有显著差异。
数据:
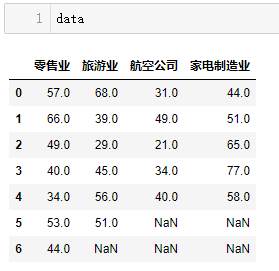
解析:
要分析四个行业之间的服务质量是否有显著差异,实际上也就是要判断行业对被投诉次数是否有显著影响,做出这种判断最终被归结为检验着四个行业被投诉次数的均值是否相等。如果它们的均值相等,就意味着行业对被投诉次数是没有影响的,也就是它们之间的服务质量没有显著差异,如果均值不全相等,意味着行业对被投诉次数是由影响的,他们之间的服务质量由显著差异。
- SST : 反映全部数据误差大小的平方和称为总平方和
- S S T = ∑ i = 1 k ∑ j = 1 n i ( x i j − x ˉ ˉ ) 2 SST = \sum^k_{i=1} \sum^{n_i}_{j=1}(x_{ij}-\bar{\bar{x}})^2 SST=∑i=1k∑j=1ni(xij−xˉˉ)2
- SSE : 反映组内误差大小的平方和称为组内平方和,也称为误差平方和或残差平方和
- S S E = ∑ i = 1 k ∑ j = 1 n i ( x i j − x ˉ i ) 2 SSE=\sum^k_{i=1} \sum^{n_i}_{j=1}(x_{ij}-\bar{x}_i)^2 SSE=∑i=1k∑j=1ni(xij−xˉi)2
- MSE:SSE的均方,业称为组内均方或组内方差
- M S E = 组 内 平 方 和 自 由 度 = S S E n − k MSE = \frac{组内平方和}{自由度}=\frac{SSE}{n-k} MSE=自由度组内平方和=n−kSSE
- SSA : 反映组间误差大小的平方和称为组间平方和,也称为因素平方和
- S S A = ∑ i = 1 k n i ( x ˉ − x ˉ ˉ ) 2 SSA = \sum^k_{i=1}n_i(\bar{x}-\bar{\bar{x}})^2 SSA=∑i=1kni(xˉ−xˉˉ)2
- MSA:SSA的均方,业称为组间均方或组间方差
- M S A = 组 间 平 方 和 自 由 度 = S S A k − 1 MSA = \frac{组间平方和}{自由度}=\frac{SSA}{k-1} MSA=自由度组间平方和=k−1SSA
假设
设零售业被投诉次数的均值为
μ
1
\mu_1
μ1,
旅游业被投诉次数的均值为
μ
2
\mu_2
μ2,
航空公司被投诉次数的均值为
μ
3
\mu_3
μ3,
家电制造业被投诉次数的均值为
μ
4
\mu_4
μ4,
- H 0 : μ 1 = μ 2 = μ 3 = μ 4 H_0:\mu_1=\mu_2=\mu_3=\mu_4 H0:μ1=μ2=μ3=μ4 自变量对因变量没有显著影响
- H 1 : μ i ( 不 全 相 等 ) H_1:\mu_i(不全相等) H1:μi(不全相等) 自变量对因变量有显著影响
from scipy import stats
import numpy as np
import pandas as pd
n = data.count().sum()
k = len(data.columns)
#显著性水平
a = 0.05
x_bar_bar = data.sum().sum()/n
SST = np.power(data-x_bar_bar,2).sum().sum()
SSA = (np.power(data.mean()-x_bar_bar,2)*data.count()).sum()
SSE = np.power(data-data.mean(),2).sum().sum()
MSA = SSA/(k-1)
MSE = SSE/(n-k)
计算检验统计量F
F = M S A M S E − − F ( k − 1 , n − k ) F = \frac{MSA}{MSE} --F(k-1,n-k) F=MSEMSA−−F(k−1,n−k)
F = MSA/MSE
F
3.4066426904716036
做出统计决策
依据统计量决策
# F 分布临界值
F_a = stats.f.isf(a,k-1,n-k)
F_a
3.127350005113399
依据p值决策
p_value = stats.f.sf(F,k-1,n-k)
p_value
0.03876452440122184
根据上面的计算结果,显著性水平 a=0.05,F > F_a,p值 < a。
因此拒绝原假设,表明行业对被投诉次数有显著影响。
关系强度的测量 R 2 R^2 R2
R 2 = S S A S S T R^2 = \frac{SSA}{SST} R2=SSTSSA
R_2 = SSA/SST
R_2
0.34975883740838953
- R 2 R^2 R2表明,自变量(行业)对因变量(被投诉次数)的影响占总效应的34.97%,而残差效应则占65%。
- 也就是说,行业对被投诉次数差异解释的比例达到35%,而其他因素所解释的比例为65%.
- 尽管 R 2 R^2 R2并不高,但行业对被投诉次数的影响已经达到了统计上显著的程度。
根据 R 2 R^2 R2值得出相关系数r
- |r|>=0.8,高度相关
- 0.5<=|r|<0.8,中度相关
- 0.3<=|r|<0.5,低度相关
- |r|<0.3,相关程度极弱,可视为不相关
r = np.sqrt(R_2)
r
0.5914041235977219
根据相关系数r,表明行业与被投诉次数之间有中等以上的关系
方差分析中的多重比较
通过前面的分析得出的结论是:不同行业被投诉次数的均值不完全相同。
但究竟哪些均值之间不相等?这种差异到底出现在哪些行业之间?
这就需要做进一步的分析,所使用的方法就是多重比较法(multiple comparison procedures)
这里使用LSD,最小显著差异法(least significant difference)
L
S
D
=
t
a
/
2
M
S
E
(
1
n
i
+
1
n
j
)
LSD = t_{a/2} \sqrt{MSE(\frac{1}{n_i}+\frac{1}{n_j})}
LSD=ta/2MSE(ni1+nj1)
第一步,提出假设
- 检验1: H 0 : μ 1 = μ 2 , H 1 : μ 1 ≠ μ 2 H_0:\mu_1=\mu_2,H_1:\mu1 \neq \mu_2 H0:μ1=μ2,H1:μ1=μ2
- 检验2: H 0 : μ 1 = μ 3 , H 1 : μ 1 ≠ μ 3 H_0:\mu_1=\mu_3,H_1:\mu1 \neq \mu_3 H0:μ1=μ3,H1:μ1=μ3
- 检验3: H 0 : μ 1 = μ 4 , H 1 : μ 1 ≠ μ 4 H_0:\mu_1=\mu_4,H_1:\mu1 \neq \mu_4 H0:μ1=μ4,H1:μ1=μ4
- 检验4: H 0 : μ 2 = μ 3 , H 1 : μ 2 ≠ μ 3 H_0:\mu_2=\mu_3,H_1:\mu2 \neq \mu_3 H0:μ2=μ3,H1:μ2=μ3
- 检验5: H 0 : μ 2 = μ 4 , H 1 : μ 2 ≠ μ 4 H_0:\mu_2=\mu_4,H_1:\mu2 \neq \mu_4 H0:μ2=μ4,H1:μ2=μ4
- 检验6: H 0 : μ 3 = μ 4 , H 1 : μ 3 ≠ μ 4 H_0:\mu_3=\mu_4,H_1:\mu3 \neq \mu_4 H0:μ3=μ4,H1:μ3=μ4
第二步,计算检验统计量
x1_bar = data.零售业.mean()
x2_bar = data.旅游业.mean()
x3_bar = data.航空公司.mean()
x4_bar = data.家电制造业.mean()
n1 = data.零售业.count()
n2 = data.旅游业.count()
n3 = data.航空公司.count()
n4 = data.家电制造业.count()
# 检验1
t_1 = abs(x1_bar-x2_bar)
# 检验2
t_2 = abs(x1_bar-x3_bar)
# 检验3
t_3 = abs(x1_bar-x4_bar)
# 检验4
t_4 = abs(x2_bar-x3_bar)
# 检验5
t_5 = abs(x2_bar-x4_bar)
# 检验6
t_6 = abs(x3_bar-x4_bar)
第三步,计算 LSD
t_a2 = stats.t.isf(a/2,n-k)
t_a2
# 检验1
LSD_1 = t_a2*np.sqrt(MSE*(1/n1+1/n2))
# 检验2
LSD_2 = t_a2*np.sqrt(MSE*(1/n1+1/n3))
# 检验3
LSD_3 = t_a2*np.sqrt(MSE*(1/n1+1/n4))
# 检验4
LSD_4 = t_a2*np.sqrt(MSE*(1/n2+1/n3))
# 检验5
LSD_5 = t_a2*np.sqrt(MSE*(1/n2+1/n4))
# 检验6
LSD_6 = t_a2*np.sqrt(MSE*(1/n3+1/n4))
第四步,做出决策
检验1 :
t_1 < LSD_1
不拒绝H_0,不能认为零售业与旅游业被投诉次数之间有显著差异
检验2:
t_2 < LSD_2
不拒绝H_0,不能认为零售业与航空公司被投诉次数之间有显著差异
检验3:
t_3 < LSD_3
不拒绝H_0,不能认为零售业与家电制造业被投诉次数之间有显著差异
检验4 :
t_4 < LSD_4
不拒绝H_0,不能认为旅游业与航空公司被投诉次数之间有显著差异
检验5 :
t_5 < LSD_5
不拒绝H_0,不能认为旅游业与家电制造业被投诉次数之间有显著差异
检验6 :
t_6 > LSD_6
拒绝H_0,认为航空公司与电制造业被投诉次数之间有显著差异

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










