数据结构与算法概念与理解

1、数据结构与算法

编程语言、数据结构与算法的关系

两个层次的掌握：

• 知其然：掌握算法分析方法（第2章）和八大算法（蛮力法、分治法、减治法、动态规划法、贪心法、回溯法、分支限界法和概率法）的设计思路和经典例子
• 知其所以然：熟知和理解各种算法的设计思路，应用于解决实际问题

程序=算法+数据
算法：程序的灵魂，解决一个问题采用的方法和步骤

1.1、算法特性

一个好的算法通常具有以下特性：

• 正确性：得到正确或者近似的结果
• 健壮性：抵抗尽可能多的错误或不合法输入的影响
• 可理解性：一看就懂，一懂就能实现
• 抽象分级：简练，数据合理分类
• 高效性：时间复杂度（快），空间复杂度（省）

1.2、算法的描述方法

• 自然语言：文字描述
• 流程图：用框图和流程线描述
• 结构化流程图：改进的流程图
• N-S图：简洁的流程图
• 伪代码：擅于设计算法时对算法的描述
• 计算机语言：用语言实现算法（c语言或java语言）

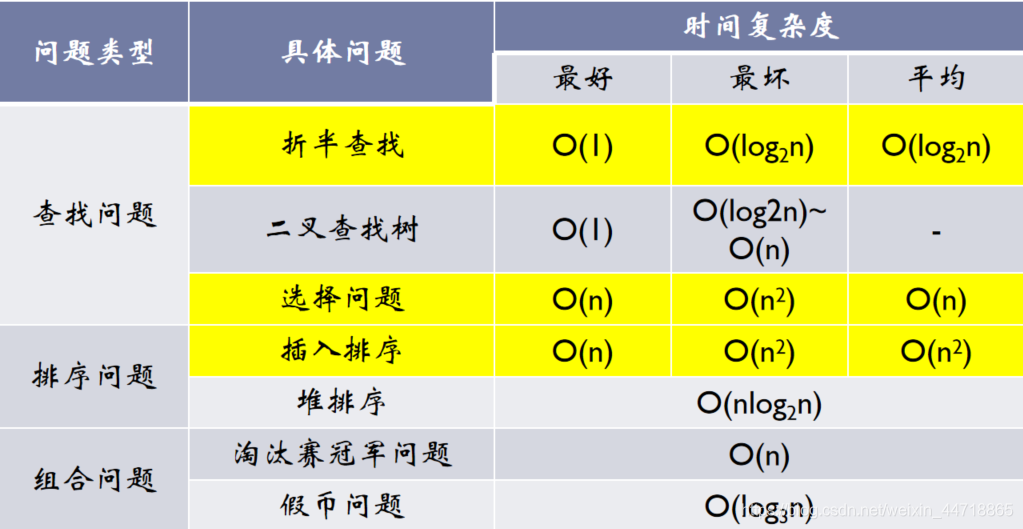
1.3、查找问题的经典算法

• 二分查找
• 顺序查找
• 串匹配问题
• 折半查找
• 二叉查找树

1.4、排序问题的经典算法

• 选择排序
• 起泡排序
• 归并排序
• 快速排序（重要）
• 插入排序
• 堆排序

1.5、图问题

• 哈密顿回路
• TSP问题（特殊的哈密顿回路：路径最短）
• 最短路径问题（单源点最短路径问题、多段图最短路径问题、多源点最短路径问题）
• 图着色问题
• 最小生成树问题

1.6、组合问题

• 0/1背包问题
• 最大子段和问题
• 八皇后问题

1.7、集合问题

• 最近对问题
• 凸包问题

2、时间复杂度

2.1、概念

• 执行算法的快慢与什么有关：硬件因素、软件因素

• 排除软硬因素，算法的执行速度随执行语句数量增加而就增加。

• 基本语句：最重要的语句，主要来源于循环结构（循环体内若有条件结构，则条件部分为基本语句，条件部分若包含循环结构，要具体分析访问循环结构的次数。）
  
  

• 输入规模：影响基本语句的执行次数的变量，通常来说，输入规模越大，算法的计算复杂度越长
  

• 时间复杂度函数T（n）：算法基本语句的执行次数，变量n为输入规模
• 时间复杂度O(n)
• 非递归算法的时间复杂度分析
  
  

2.2、非递归算法的时间复杂度

2.3、递归算法的时间复杂度

2.4、算法的空间复杂性分析

3、蛮力法

3.1、设计思路

• 基本思想：遍历所有取值，选出符合任务要去的解。
• 最简单，最容易想到的方法，几乎能解决所有的问题。
• 时间复杂度往往最高
• 蛮力法是最笨的方法。

3.2、步骤

3.3、应用

3.4、查找问题

3.4.1、顺序查找

顺序查找

• 可从头向尾查找，也可从尾向头查找
• 若从尾向头查找，可通过设置哨兵值减少越界的判定
• 最好：O(1)；最坏：O(n)；平均：O(n)
  
  
  
  

3.4.2、串匹配问题

• BF算法
  （1）每次匹配失败，模式串往后移一位，从头开始进行下一次匹配
  （2）时间复杂度为O(mn)，与主串和模式串长度有关
• KMP算法
  （1）利用模式串本身的相似性，去除多余的匹配
  （2）next数组的创建
  （3）匹配算法
  当匹配不成功时，主串不回溯，模式串回溯到next[j]，其中j是指不匹配的字符在模式串中的位置
  若next[j]=-1，主串下标往向移一位，模式串从头开始匹配
  （4）时间复杂度：O(m+n)，生成next的函数采用《阅读材料》的方法

暴风BF算法过程：使用子串T去匹配原串S中的元素，T从头开始，S也从头开始，T匹配的元素跟S元素不匹配时，T从头开始，S从上次开始的下个元素开始，基础使用T所有元素去匹配S。直到找到子串T为止。

KMP算法过程：

• 求next数组：下标为0的元素值为-1，下标为1的元素值为0，下标为2的元素的值为取子串中的前两个元素看可不可弄出对称元素，对称元素个数为下标为2的元素值，例如aa，则值为1，aba值1，aaaa值为2；后面的计算跟下标为2一样。
• 匹配过程：子串和文本都从头开始，计算到不匹配的元素的时候，看子串那个不匹配的元素的下标为多少，取子串下标元素的next值，比如在子串的第四个元素也是下标为3的元素不匹配，则next[3]=1；得出的next数组的值作为子串T从文本S的哪个位置开始，比如next[3]=1;则从文本S的第二个元素开始匹配T。
  
  

3.5、排序问题

3.5.1、选择排序

基本思想：

• 将序列划分成有序区（左边）和无序区（右边）
• 初始时，有序区为空，无序区为序列全部
• 每一次选择出无序区中最小元素，与无序区中第1个元素交换，成为有序区的最后一个元素

真题：对数据48,70,8,30,23,11,15进行选择排序，写出每趟的结果
解：每次都从无序区中选择最小元素与无序区第一个元素交换成为有序区末尾
初始： （）48,70,8,30,23,11,15
第1趟：（8）70,48,30,23,11,15
第2趟：（8,11）48,30,23, 70,15
第3趟：（8,11,15）30,23, 70,48
第4趟：（8,11,15,23）30, 70,48
第5趟：（8,11,15,23,30）70,48
第6趟：（8,11,15,23,30,48）70

3.5.2、起泡排序

基本思想：

• 将序列划分成有序区（右边）和无序区（左边）
• 初始时，有序区为空，无序区为序列全部
• 每一次“起泡”相邻元素依次两两比较，将较大/小者交换到后面，成为有序区的第一个元素

例：采用起泡排序法对数据48,70,8,30,23,11,15进行升序排序，写出每趟的结果
解：
初始： 48,70,8,30,23,11,15（）
第1趟起泡：
48,70,8,30,23,11,15
48,8,70,30,23,11,15
48,8,30,70,23,11,15
48,8,30,23,70,11,15
48,8,30,23,11,70,15
48,8,30,23,11,15,（70）
第2趟起泡：
8,48,30,23,11,15,（70）
8,30,48,23,11,15,（70）
8,30,23,48,11,15,（70）
8,30,23,11,48,15,（70）
8,30,23,11,15,（48, 70）
第3趟起泡：
8,30,23,11,15,（48, 70）
8,23,30,11,15,（48, 70）
8,23,11,30,15,（48, 70）
8,23,11,15,（30,48, 70）
第4趟起泡：
8,23,11,15,（30,48, 70）
8,11,23,15,（30,48, 70）
8,11,15,（23,30,48, 70）
第5趟起泡：
8,11,15,（23,30,48, 70）
8,11,（15,23,30,48, 70）
第6趟起泡：
8,（11,15,23,30,48, 70）

3.6、组合问题

3.6.1、0/1背包问题

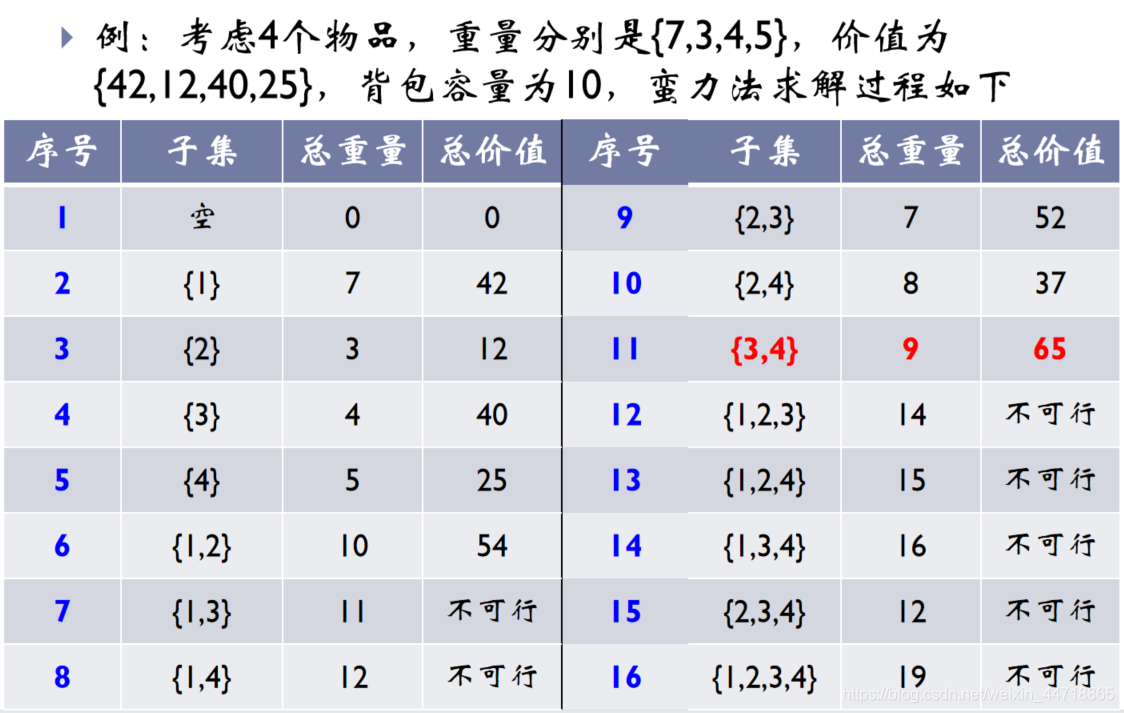
问题描述：给定n个不同重量不同价值的物品和一个容量一定的背包，设计方案使得在不超出背包容量的前提下，装进背包的物品总价值最高。

• 如果用0表示物品不装进去，1表示物品装进去，则问题变成对每个物品指定0或者1的过程，所以称为0/1背包问题
• 背包问题是0/1背包问题的一般化，即物品可以部分装到包里

蛮力法求解基本思想：穷举所有装包的方案，选择价值最高的一个

3.6.2、任务分配问题

问题描述：假设有n个任务分给n个人执行，每个人只能执行一个任务且执行不同任务的成本不同，求一个分配方法，使得总成本最小

想法：列出所有可能的分配方案，逐个去检验其成本，选择成本最小的一个方案

3.7、图问题

3.7.1、哈密顿回路问题（周游世界问题）

问题描述：在给定的N个城市以及城市间的通路，要求找出一条线路，使得从一个城市出发，经过每个城市恰好一次，然后回到出发城市。


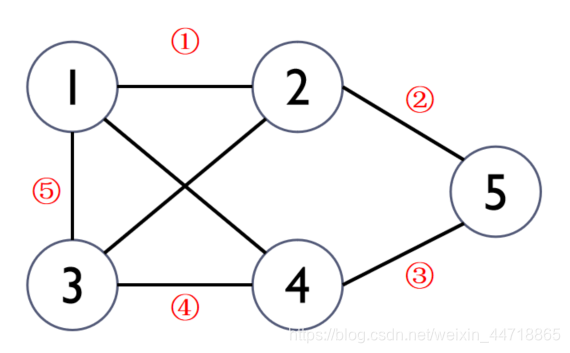
想法：

• 不考虑结点与结点之间是否连通，n个结点遍历一遍再回到原点的可能性共有n!个；例：3个城市，可能的哈密顿回路有以下3!=6条，分别是：
  1→2→3→1
  1→3→2→1
  2→1→3→2
  2→3→1→2
  3→1→2→3
  3→2→1→3
• 依次检验各种方案是否符合哈密顿回路的条件：
  （1）相邻顶点之间存在边
  （2）最后一个顶点与第一个点之间存在边

3.7.2、TSP问题

问题描述： TSP(Travelling Salesman Problem)，遍历n个城市，且要求所走路程最短，是一个特殊的哈密顿回路问题

TSP问题 VS 哈密顿问题

• 相同点：都要求从一个城市出发，遍历所有城市一次，再回到第一个城市
• 不同点：哈密顿问题在无向图中进行；TSP问题在带权无向图中进行（因为要算最短路程）

想法：与哈密顿回路想法相近
（1）穷举所有遍历各城市的方案
（2）分别检查当前方案是否构成哈密顿回路，如果是，则计算当前方案的路程，并检查是否路程最短

算法分析
（1）对指定出发城市的TSP问题，总共的方案数为：(n-1)!个
（2）每个方案需要检查是否为哈密顿回路，需要循环最多n条路径
（3）总计算量T(n)=n*(n-1)!=n!=O(n!)

注意： 在各方案中，有一半路径相同，只是方向相反，比如：1-3-2-5-4-1和1-4-5-2-3-1，因此可以只算一半的路径，但时间复杂度仍为O(n!)

3.8、几何问题

3.8.1、最近对问题

问题描述：在一堆散点集中，找出距离最短的一对点

想法： 对所有点两两计算其欧几里德距离，取其中最短的一对点作为输出
两个点(xA,yA)和(xB,yB)的欧几里德距离d(A,B)为：

3.8.2、凸包问题

Before 凸包，什么是凸？

定义： 一个图形是凸图形，当且仅当图形内任意两点的连线，都包含在该图形内


凸包问题：点集的最小凸多边形构造问题

• 在点集中找出一个子集，使得这些子集中各点相连构成一个凸图形（凸多边形），刚好把所有点集包含
• 下图p1-p8构成了点集的一个凸包，称为极点
  
  想法：
• 考虑构成凸包的边的特点：所有点集都位于该边划分出来的一边
• 设p1和p2的坐标分别是(x1,y1)和(x2,y2)，则该两点确定的直线方程为：
  
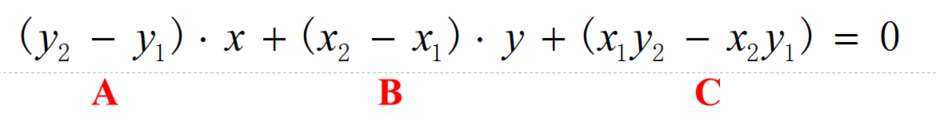
• 设点集中的两个点，其确定的直线方程为Ax+By+C=0。若所有点集都在该直线的一边，即Ax+By+C≥0或Ax+By+C≤0，则该两点为凸包上的两个极点
  

3.9、总结

（1）蛮力法的基本思想：
遍历所有自变量的取值，搜索满足任务要求的解

（2）蛮力法的设计思路：
确定自变量及其变化范围
根据任务已知条件去除冗余的穷举量

（3）蛮力法的特点：简单、慢、万能

4、分治法

4.1、分治法的基本思想

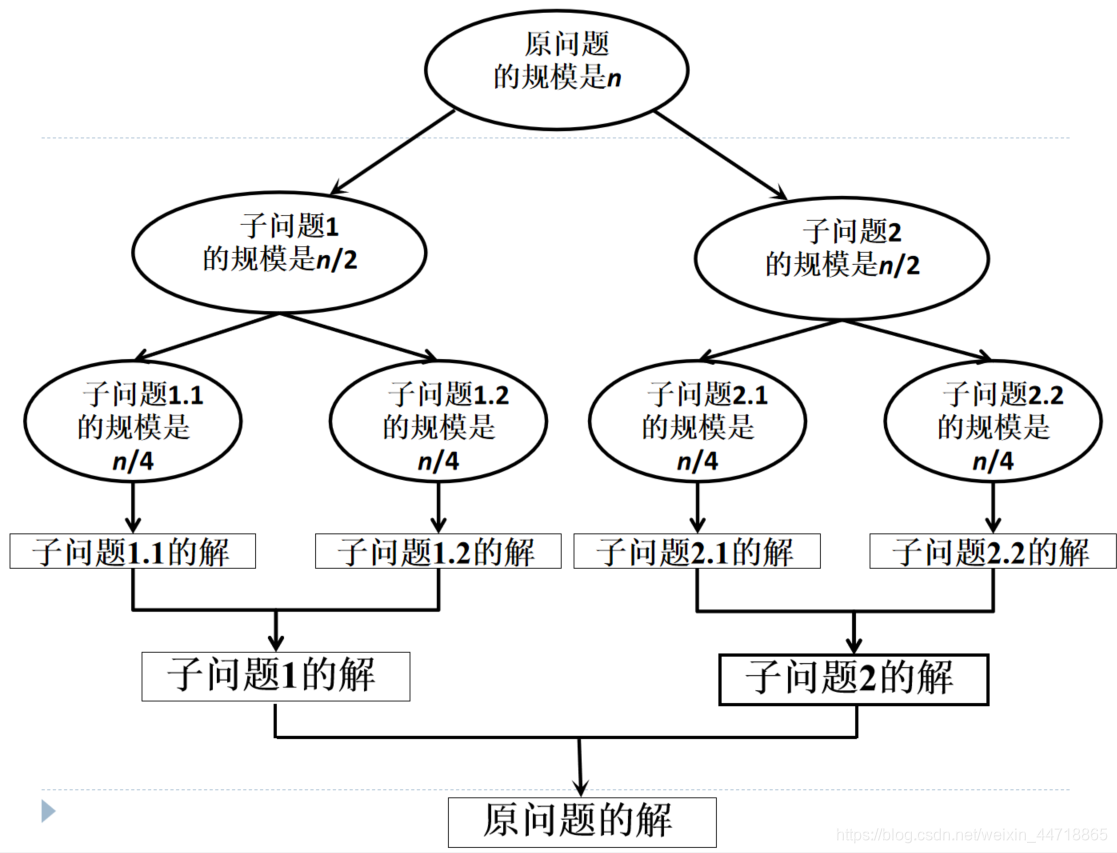
分治法求解问题的主要步骤：划分，求解，合并
（1）问题划分。将规模为n的问题划分成k个子问题
细节：

• 如果子问题规模仍然很大，可以再继续划分3^2可继续划分成2个 3的1次方相乘
• 每个子问题的规模尽可能相等（平衡子问题），便于用相同的方法去求解子问题3的4次方划分成3的2次方，再划分成3的1次方，都在算3的幂次方
• 每个子问题间尽可能独立（独立子问题），若不独立，需要另外处于公共子问题（最大子段和）

（2）求解子问题。各子问题的求解方法相同，通常采用递归方法实现。f(n)→f(n/2)→f(n/4)……
（3）合并子问题的解。将各子问题的解逐层合并，得到问题的最终解

4.2、排序问题

4.2.1、归并排序

基本思想：
将序列划分成两个长度相等的子序列，分别进行排序，最后将两个有序序列合并

步骤：

• 将序列分成两段相等长度的子序列
• 从两段序列的第一个元素开始比较两段序列的元素，取当前较小的值为新序列的元素
• 将采纳的子序列下标向后移动，采纳的元素添加到新的队列中。
• 当其中一个序列全部移动到新序列后，剩余序列直接拷贝
  
  真题：对数据48,70,8,30,23,11,15,28进行归并排序，写出每趟的结果
  ① 划分：
  48,70,8,30 23,11,15,28
  48,70 8,30 23,11 15,28
  48 70 8 30 23 11 15 28

② 求解子问题，并合并子问题：
第一趟： 48 70 8 30 23 11 15 28
第二趟： 48,70 8,30 11,23 15,28
第三趟： 8,30,48,70 11,15,23,28
第四趟： 8,11,15,23,28,30,48,70

4.2.2、快速排序

基本思想：
（1）划分：选定一个数做为轴值，把序列分成比轴值小（左边）和比轴值大（右边）两个子序列

• 选定第一个元素作为轴值，下标用i标记，后面的元素用j标记；从后面和前面比较，后面的值比轴值大就后面的下标向前移动一位，如果后面的比前面的小，那么两个元素交换位置，前面的下标向后移动一位；交换后之前是轴值有j标记，所以下次比较如果后面的大于前面的就是i向后移动不是j向前移动。
• 当i和j重合时结束
  
  （2）求解子问题：分别对两个子序列进行轴值划分
  （3）合并：不需要合并！！

关于快速排序的你可能不知道的事
（1）快速排序的适用场合
根据时间复杂度分析，快速排序对已有序（不管是正序还是逆序）的序列，效率最差。

（2）快速排序属于“有序度增长法”，虽然每次划分得到的序列并非有序，但每次划分实质上是找出轴值在排序后的位置，即每次划分是对轴值进行排序

（3）假如某次划分后，轴值所在位置为i，实质上表明该轴值在序列中是第i小的值（注意，这里说的序列是参与划分的序列），因此可借助快速排序的划分操作实现“求序列第i小数”

例：采用排序方法对以下序列进行排序，写出每一趟的排序结果：
48,70,8,30,23,11,15,28
解：
初始： 48,70,8,30,23,11,15,28
第一趟： [28,15,8,30,23,11],(48),[70]
第二趟： [11,15,8,23],(28),[30],(48),[70]
第三趟： [8],(11),[15,23],(28),[30],(48),[70]
第四趟： (8,11),[15,23],(28),[30],(48),[70]
第五趟： (8,11,15),[23],(28),[30],(48),[70]
第六趟： (8,11,15,23,28),[30],(48),[70]
第七趟： (8,11,15,23,28,30,48),[70]
第八趟： 8,11,15,23,28,30,48,70

加粗 表示轴值；
圆括号表示已经排好的数
中括号表示待排序的区

4.3、组合问题

4.3.1、最大子段和问题

问题：
给定由n个整数（可能有负整数）组成的序列，的到其中一个连续的子序列（子段），使得该子段的和是所有连续子段中最大，如-20，11，-4，13，-5，-2

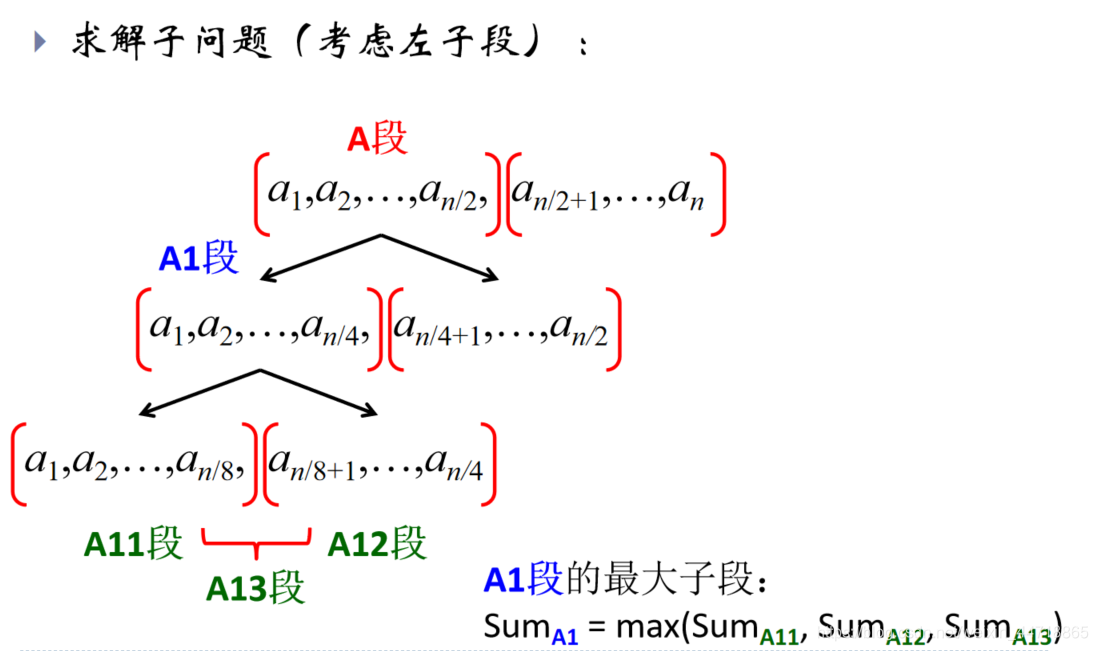
采用分治法求解最大子段和问题步骤：
（1）划分：将序列划在长度相等的两段

3种情况：
① 最大子段和出现在A段；
② 最大子段和出现在B段；
③ 最大子段和一部分在A段，另一部分在B段。

想法：

（1）分别找出上述3种情况的最大子段和：设A段的最大子段和为SumA，B段的为SumB，跨越AB段的最大子段和为SumC
（2）整段序列的最大子段和必为上面3个子段和的最大值，即MaxSum = max(SumA, SumB, SumC)



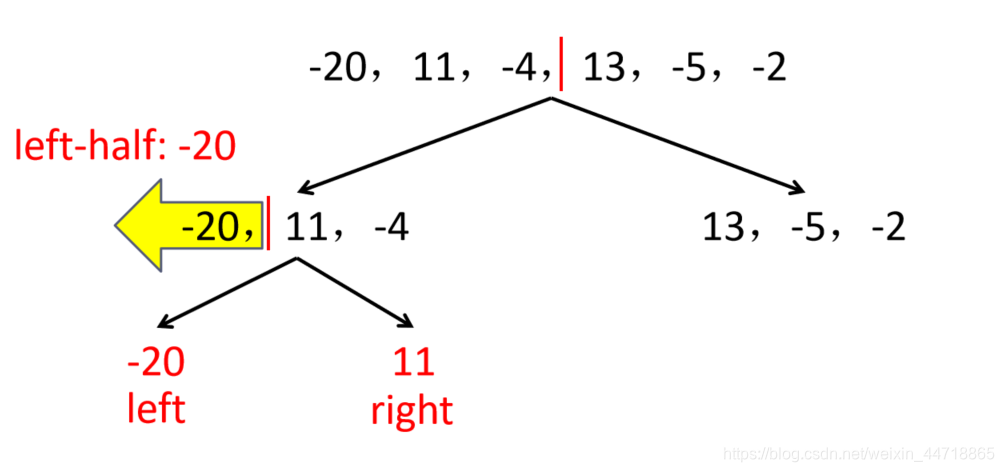
例：求以下序列的最大子段和
-20，11，-4，13，-5，-2
解：先求左子段，再求右子段，最后求跨子段

4.3.2、棋盘覆盖问题

问题描述：
在一个2k*2k个方格组成的棋盘中，恰有一个方格与其它方格不同，要求用不同角度的L形图形填充剩下的方格


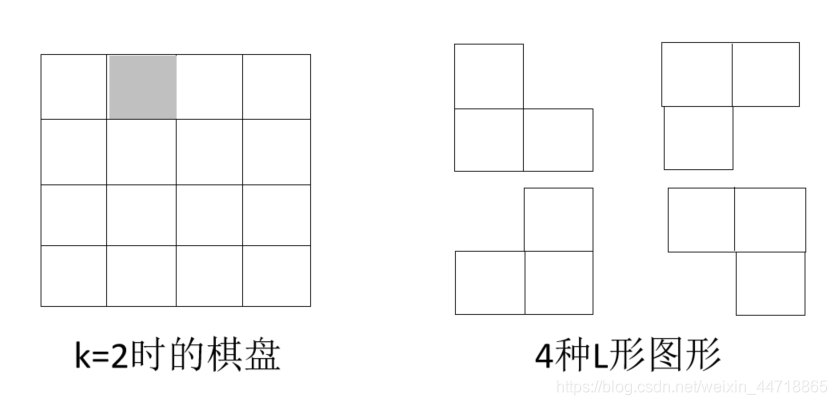
想法：
（1）划分：将棋盘划分成相等的四份，特殊的方格只会落在其中一份中
（2）将有特殊方格的一份继续平分为四份。经过多次划分后，肯定会出现一个L形图形和一个特殊方格的情况

（3）为了让上述划分同样适用于其它方格，在每次划分后，对没有特殊方格的子划分接合处的方格暂时设为特殊方格

4.4、几何问题

4.4.1、最近对问题

（1）划分：将点集划分成基本相等的两个子集

（2）子问题求解：
① 最近对在S1中，最小距离为d1
② 最近对在S2中，最小距离为d2
③ 最近对的两个点分别在S1和S2中，最小距离为d(p,q)

子问题①和②采用递归方法求解：
double closest(point s[], int low, int high){
if 子集中只剩两个点P1(x1, y1)，P2(x2,y2)
计算并返回两点的距离(即最小距离)，算法结束；

if 子集中有三个点P1(x1,y1)，P2(x2,y2)，P3(x3,y3)
{ 分别计算三个点相互的距离d(P1,P2), d(P1,P3)和d(P2,P3)
返回三个距离中的最小值，算法结束；
}
注意：要特别处理三个点的情况，是因为三个点继续划分，会出现孤立点，不能形成距离

4.4.2、凸包问题

4.5、总结

分治法的基本思想：将原问题划分成若干个规模较小的子问题，通过求解各子问题来得到原问题的解

分治法的基本步骤：
（1）划分：
（1.1）平衡子问题：子问题规模尽量相同
（1.2）独立子问题：子问题尽量相互独立
（2）求解子问题：采用递归方法
（3）合并子问题的解

5、减治法

基本思想
用减治法求两个有序序列的中位数（中间大的数）
比如：S1={11,13,15,17,19}， S2={2,4,6,8,20}
则S1和S2的中位数为两个数列合并后的中位数，即：S1∪S2={2,4,6,8,11,13,15,17,19,20}
中位数为11

想法：
（1）分别求出两个序列的中位数，记为a和b。
（2）两个序列的中位数可能出现在三种位置：
① 若a=b，则a或b即为两个序列的中位数；
比如：S1={11,13,15,17,19}，其中位数为a=15；
S2={2,4,15,18,20}，其中 位数为b=15。
S1∪S2={2,4,11,13,15, 15,17,18,19,20}
两个序列的中位数为a或b=15
② 若a<b，则中位数出现在[a, b]之间：
比如：S1={11,13,15,17,19}，其中位数为a=15；
S2={16,18,20,28,40}，其中 位数为b=20。
S1∪S2={11,13,15, 16,17,18,19,20,28,40}
两个序列的中位数在[15,20]范围内
注意：只需要考虑S1序列中位数(15)以后的数，及S2序列中位数(20)以前的数
③ 若a>b，则中位出现在[b, a]之间：
比如：S1={16,18,20,28,40}，其中位数为a=20；
S2={11,13,15,17,19}，其中 位数为b=15。
S1∪S2={11,13,15, 16,17,18,19,20,28,40}
两个序列的中位数在[15,20]范围内
（3）重复第（2）步，直到两个序列都只有一个元素时，取两者较小者。

减治法的体现在于，每次求解，问题的规模都减少一半，而原问题的解就在这一半的子问题中

假如两个序列长度为n，每次迭代减少一半，一共经过log2n次后，序列长度变为1。每次迭代的任务是计算中位数位置，然后重置序列的开始和结束位置，均为O(1)

因此，其时间复杂度为O(log2n)。

5.1、折半查找

在有一个有序序列中查找值为k的记录。若查找成功，返回记录k所在的位置，否则，返回失败信息
想法： 将待查找的数k与序列的中位数mid进行比较：
① 若k = rmid，返回结果；
② 若k < rmid，表明k在rmid往前的半段子序列中，下一步在前半段中寻找k；
③ 若k > rmid，表明k在rmid往后的半段子序列中，下一步在后半段中寻找k

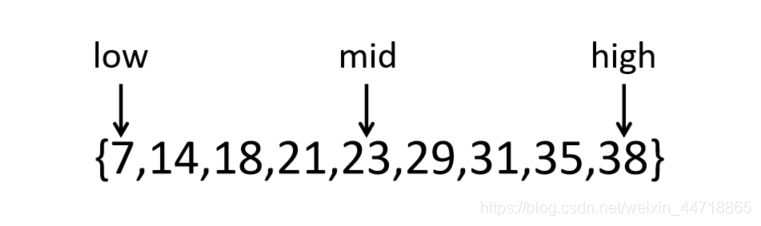
例：采用折半查找法在以下有序序列中查找29的过程
{7,14,18,21,23,29,31,35,38}
解：
①k= 29, low=0, high=8,mid=(low+high)/2=4
k与rmid比较；k>rmid；取mid往后的后半段；
②k= 29, low=5, high=8,mid=(low+high)/2=6；
k与rmid比较；k<rmid;取mid往前的前半段。
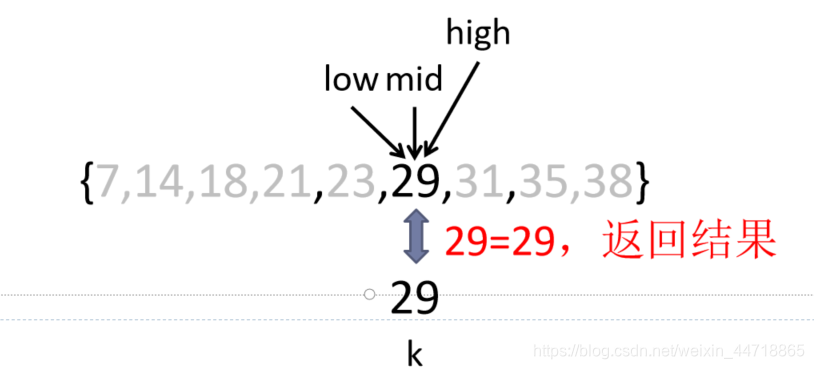
③k= 29, low=5, high=5,mid=(low+high)/2=5
k与rmid比较，k=rmid；返回结果

时间复杂度分析
① 最好情况：序列中值即为待查找的数，比较1次
② 最坏情况：待查找的数需要一直折半，直到最后折半后的区域只乘一个元素时，才是待查找数或者也不是查找数。此时共比较的次数为折半的次数，为⌈log2n⌉
③ 平均情况
假设待查找的数是下列树结点中的其中一个，则可能的情况有n种，故pi = 1 / n；
若待查找的数是第i个结点，则若比较的次数为其在树中的层数。

5.2、二叉查找树

定义：二叉查找树是具有以下性质的二叉树：
① 若它的左子树不空，则左子树上所有结点的值均小于根结点的值；
② 若它的右子树不空，则右子树上所有结点的值均大于根结点的值；
③ 它的左右子树也是二叉排序树

二叉查找树的建立——根据二叉查找树的定义来建立，依次对输入的数据建立查找树


基于二叉查找树的查找算法：
（1）若root是空树，则查找失败；
（2）k=根结点的值，则查找成功；
（3）若k<根结点的值，则在root的左子树上查找；
（4）若k>根结点的值，则在root的右子树上查找。

在下面二叉查找树上查找83
① 跟根结点(63)比较，得到83>63，因此向右子树移动
② 跟结点(90)比较，得到83<90，因此向左子树移动
③ 跟结点(70)比较，得到83>70，因此向右子树移动
④ 跟结点(83)比较，得到83=83，查找成功

时间复杂度
查找所比较的次数实质上是二叉查找树从根结点到待查数所在结点的路径长度
① 最好情况：根结点即为待查找的数，比较1次；
② 最坏情况：与查找树的建立方式有关：
若建立查找树时以正序的方式输八，则查找树最深深度为n，而待查找数为序列的最后一个数，此时比较次数最多，为n
若查找树刚好能建立成完全二叉树，则树的最深深度为log2n
因此，最坏情况的时间复杂度在O(log2n)和O(n)之间

5.3、选择问题

问题： 设无序序列 T =(r1, r2, …, rn)，T的第k(1≤k≤n)小元素定义为T按升序排列后在第k个位置上的元素。给定一个序列T和一个整数k，寻找T的第k小元素的问题称为选择问题。特别地，将寻找第n/2小元素的问题称为中值问题。
想法：
（1）升序排序后直接读取第k个元素。采用最快的排序算法(归并排序)，其时间复杂度为O(nlog2n)
（2）采用减治法可把平均复杂度降低为O(n)：利用快速排序的划分过程
采用减治法求解选择问题的步骤：
（1）采用快速排序中的划分操作将无序序列分成两个子列，其中，轴值左侧子序列均比轴值小，轴值右侧子序列均比轴值大
（2）划分后，轴值所在的位置i实质上是轴值在序列按升序排序后所在的位置，即第i小。
（3）比较k和i：
① k=i, 表示ri即为要查找的数，返回；
② k<i, 表明要查的数比ri小，则递归在左侧子序列找第k小；
③ k>i, 表明要查的数比ri大，则递归找右侧子序列找第k小。

例： 采用减治法在序列{5,3,8,1,4,6,9,2,7}中查找第3小的过程
① 选择5为轴值，对序列进行第一次划分

② 5是序列第5小元素，由于3<5，表明第3小元素在序列左侧子序列中

③ 选择2为轴值，对左侧子序列进行第二次划分

④ 2为序列第2小元素，由于2<3，表明第3小元素在右侧子序列中

⑤ 选择4为轴值，对右侧子序列进行第三次划分

⑥ 4为序列第4小元素，由于3<4，表明第3小元素在其左侧子序列中

⑦ 选择3为轴值，对子序列进行第四次划分。由于序列中只有一个元素，则其即为第3小元素

5.4、排序问题

5.4.1、插入排序

基本思想： 依次将待排记录插入到有序区适当位置，直到全部记录插入完毕
基本思想（考虑升序排序情况）：
（1）将序列划分为有序区和无序区。有序区为序列第一个元素，无序区为剩下的元素。
（2）每一次操作都将无序区的第一个元素ri与有序区里从最后一个元素开始向前比较，直到找到第一个比ri小的元素rj，并将ri插入到rj后面；如果找不到元素比ri小，则ri要插入的位置为序列首部
（3）将ri插到rj后面，调整有序区中其它元素位置
插入排序的算法策略是减一法，即每插入一个元素后，原问题规模变成少了一个元素的子问题

例题：
对数据43,32,18,26,21,4,12,7,10,12进行插入排序，写出每趟的结果，并写出比较次数
注意：若当前数据插入到有序区最开头，与哨兵值也要比较1次

初始： (43) 32,18,26,21,4,12,7,10,12
第一趟： (32,43) 18,26,21,4,12,7,10,12 插32比较2次
第二趟： (18,32,43) 26,21,4,12,7,10,12 插18比较3次
第三趟： (18,26,32,43) 21,4,12,7,10,12 插26比较3次
第四趟： (18,21,26,32,43) 4,12,7,10,12 插21比较4次
第五趟： (4,18,21,26,32,43) 12,7,10,12 插4比较6次
第六趟： (4,12,18,21,26,32,43) 7,10,12 插12比较6次
第七趟： (4,7,12,18,21,26,32,43) 10,12 插7比较7次
第八趟： (4,7,10,12,18,21,26,32,43) 12 插10比较7次
第九趟： (4,7,10,12,12,18,21,26,32,43) 插12比较6次
共44次

5.4.2、堆排序

问题：采用堆结构来描述数据，并在此基础上实现排序
定义：堆——具有以下性质的完全二叉树：
每个结点的值都小于或等于左右孩子结点的值（小根堆）；或者每个结点的值都大于或等于其左右孩子结点的值（大根堆）。

基本思想：
（1）根据堆的特性，将待排序序列建立堆。升序排序采用大根堆；降序排序采用小根堆
（2）堆顶元素为最大值（大根堆）或最小值（小根堆），将该元素与最后一个元素交换并移入有序区
（3）调整无序区为一个堆结构
（4）重复（2）和（3）直到无序区剩一个元素
由于每次交换堆顶元素并调整堆后，无序区都是比原问题少一个元素的堆，因此堆排序也是采用减一法的设计策略
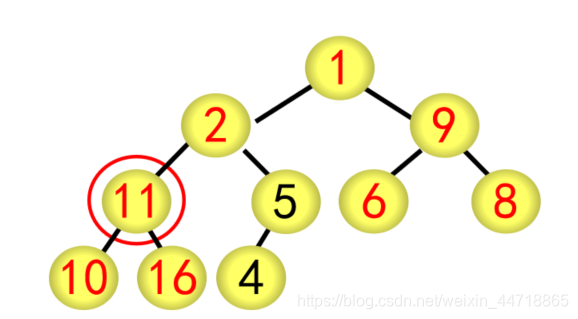
基本步骤（以序列{1,2,9,11,4,6,8,10,16,5}为例）
（1）建立堆
① 按广度优先方式建立完全二叉树，每个结点的编号按广度优先分配，如根结点为1号，最后的结点(5)为10号

② 采用筛选法调整为大根堆
对当前结点(28)，若左右子树不全为空，则与左右子树的根结点比较，将较大者移为当前结点
对移动后的结点(28)，若左右子树不全为空，继续进行上述调整，直到该结点(28)的左右子树均为空


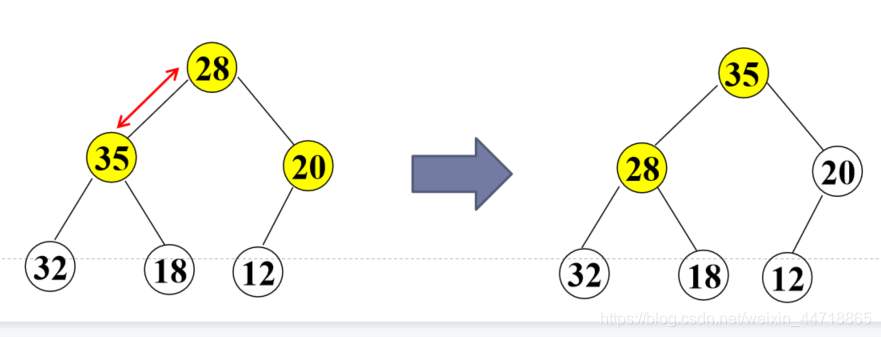
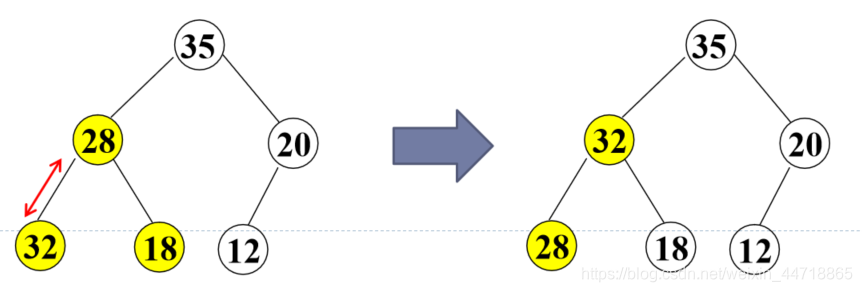
② 采用筛选法调整为大根堆，从编号为[n/2]5的结点开始往前调整








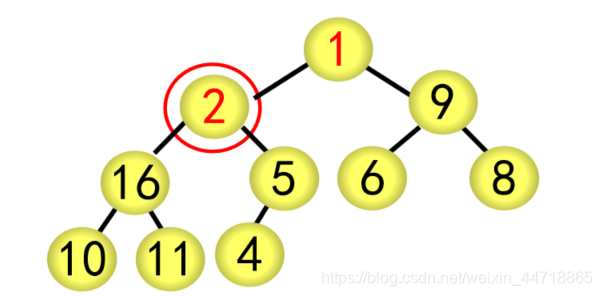
（2）交换
建立好大根堆后，堆顶元素即为最大值，将堆顶元素与最后的元素进行交换

（3）调整堆
采用筛选法对根结点进行调整

（4）重复交换与调整

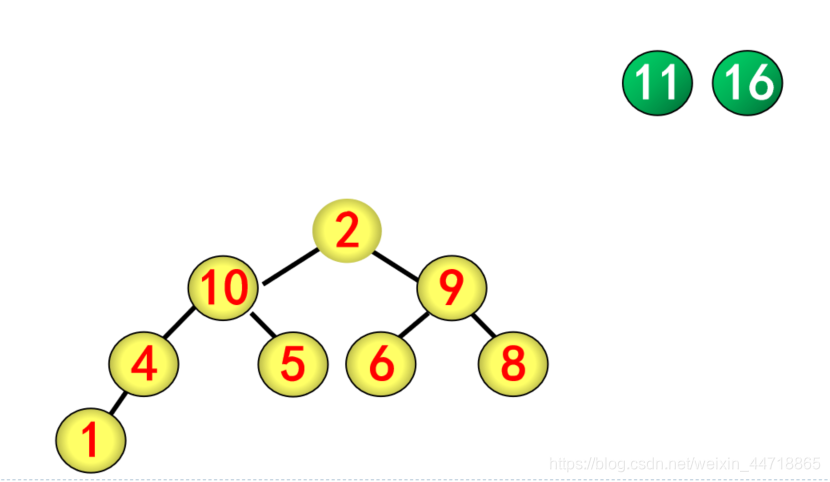
5.5、组合问题

5.5.1、淘汰赛冠军问题

淘汰赛：两队进行比赛，赢的一方继续下一场比赛；输的一方不得参加后面的比赛
（1）分治法思路：将选手分成2组（划分），分别决出两组各自的胜者（求解子问题），然后最后两组胜者再进行一次决赛（合并）。

（2）减治法思路：
将n个选手分成n/2组，每组两人。第一轮决出n/2个胜者
将n/2个选手分成n/4组，每组两人。第二轮决出n/4个胜者
以此类推，直到最后胜者只有一人，即冠军

5.5.2、假币问题

问题描述：在n枚外观相同的硬币，有一枚是假币，并且已知假币较轻。可以通过一架天平来任意比较两组硬币，从两组硬币的重量关系可推断出硬币的位置
想法1：二分法
（1）n为奇数，划分为两堆一样多的硬币[n/2]外加1个，比较两堆硬币
① 若两堆硬币等重，说明多出的1个硬币为假币；
② 若两堆硬币不等重，假币存在于较轻的一堆中，重复划分，直到找到假币
（2）n为偶数，划分出两堆数量相等的硬币[n/2]，执行（1）步中第②小步。

时间复杂度：
（1）最好情况：n为奇数，且硬币为外加的那个，O(1)
（2）最坏情况：划分到最后一个才是硬币，O(log2n)
想法2：把硬币分成3堆
① 能分成3堆，则前两堆数量为[n/3]，后一堆硬币可能是[n/3]-1或[n/3]-2。比较前两堆：
a) 若前两堆硬币等重假币在第三堆；
b) 若前两堆硬币不等重硬币在较轻的一堆，重复划分，直到找到假币。
② 不能分成3堆
a) 剩两个，则比较这两个硬币，较轻者为假币；
b) 剩一个，则为假币

时间复杂度：需要一直3分，直到剩1个或2个硬币，划分次数为O(log3n)

5.6、总结

减治法的基本思想：原问题的解可以通过规模更小的子问题的解得到，迭代缩减问题的规模，直到最后将子问题求解。

6、动态规划法

6.1、基本思想

什么样的问题可以用动态规划法解决：
（1）子问题具有重叠性——采用动态规划可以大幅度减少重复操作
（2）具有最优子结构——原问题的最优解包含了子问题的最优解，可以推导出递推式
比如：A到F的最短路径为A→B→C→D→E→F，则A到E的最短路径必然为A→B→C→D→E

设计动态规划法算法的基本思路
（1）研究问题的部分解，产生递推式
比如，问题要求f(n)，部分解为f(i), 0 ≤ i ≤ n。研究f(i)如何由i以前的值f(i-1), f(i-2) … f(0)或部分值计算得到 ，从而构造递推式。如斐波拉切序列中的f(i)=f(i-1)+f(i-2)

（2）初始值——问题规模最小时的值
比如，问题要求f(n)，其初始值可能为f(0)或f(1)等前几个；对二维情况，可能是第一行f(0,)和/或第一列f(,0)

（3）填表——根据初始值和递推关系，填写问题的所有部分解（求解子问题过程）。表中最后一个格的结果即为原问题的最优解。

（4）回溯——由于递推式中的量通常是衡量问题的一些指标，比如最短路径中的路径长度，背包问题中的价值。若要得到具体解（最短的路径或物品的选择），需要一个回溯过程
总结：
递推式、初始解、填表、回溯

6.2、数塔问题

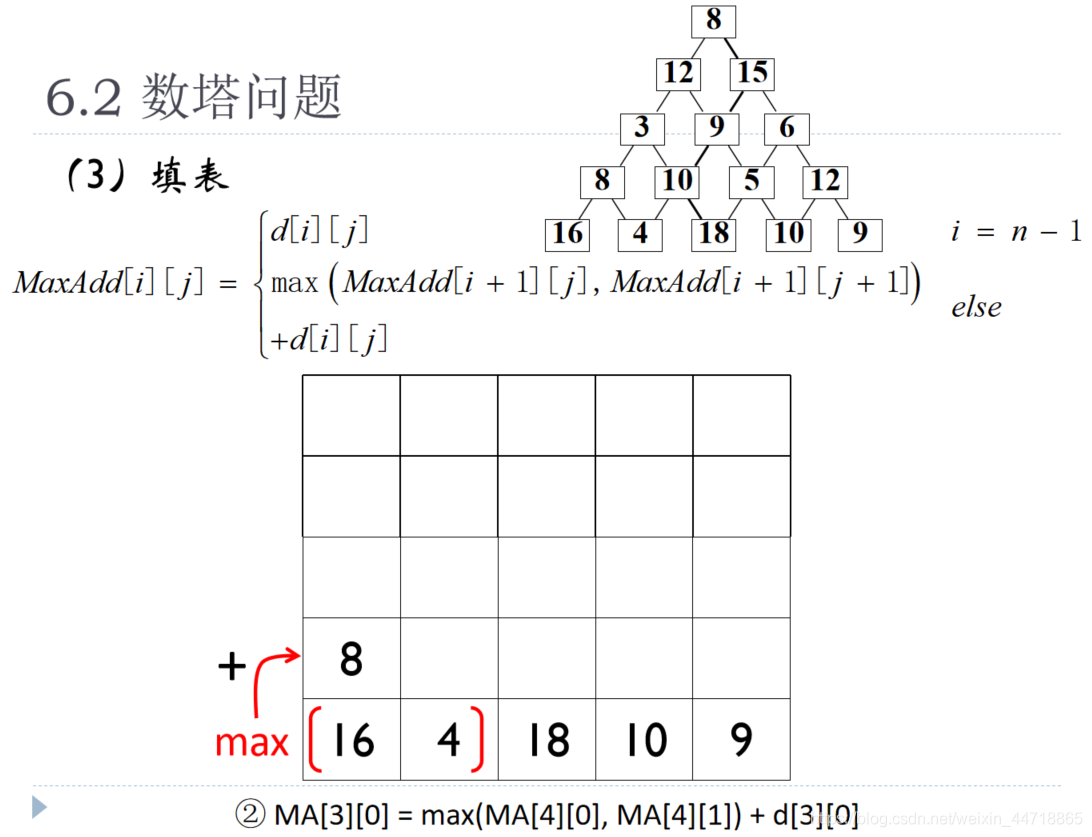
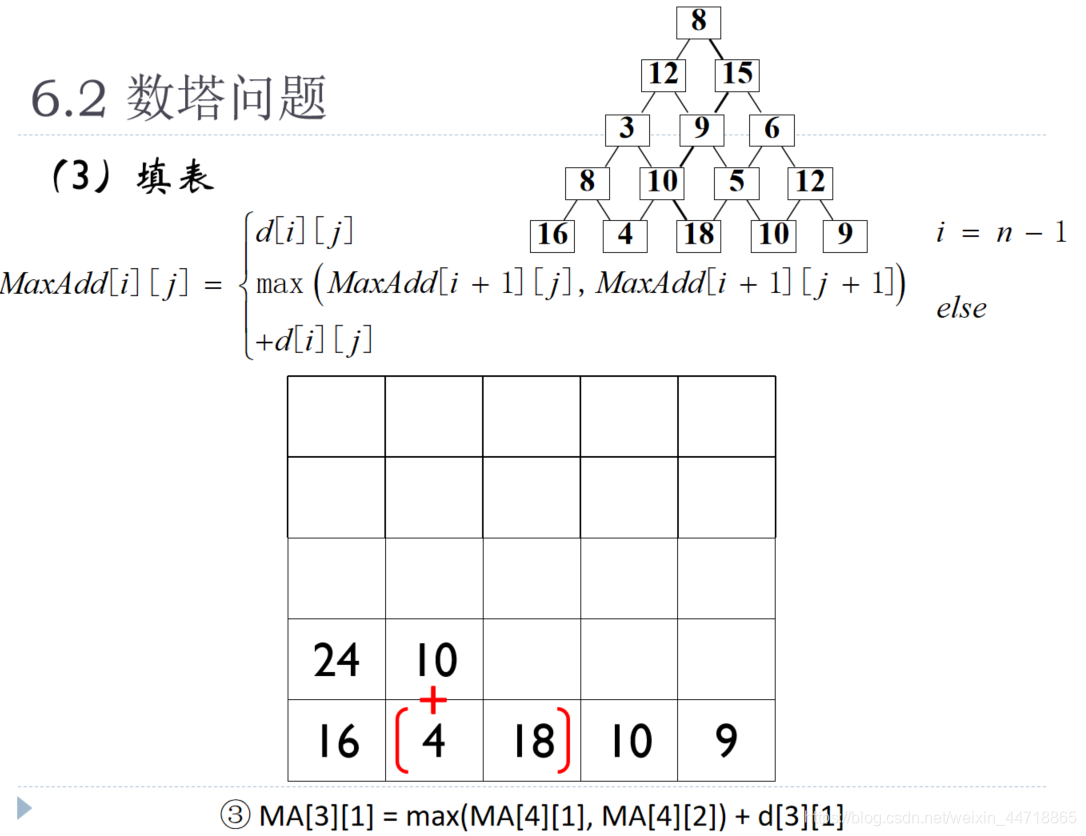
问题描述：设数塔结构如下，要求从塔顶出发，寻找一条到塔底的路径，使得该条路径上数字的和是所有路径中最大。
（0）数塔的存储方式

（1）寻找递推关系
定义MaxAdd【i】【j】表示从第i行第j列结点出发往下走所得到的最大和，研究部分解即如何根据之前的值计算MaxAdd【i】【j】

找出跟计算MaxAdd【i】【j】有关的值

分析：从【i】【j】点往下走有两条路，一条走向【i+1】【j】点，另一条走向[【i+1】【j+1】点
问题：哪条最优？
问题：哪条最优？如果从之前的结果中知道从[i+1][j]点出发的最大和(MaxAdd[i+1][j])以及从[i+1][j+1]点出发的最大和(MaxAdd[i+1][j+1]，则从[i][j]点出发的最大和是上述两个和的最大值加上[i][j]的值，即

（2）初始值
只有一个元素的数塔→底层元素MaxAdd[n-1][j]，其往下走的最大和即自己，因此有

6.3、0/1背包问题

问题描述：

给定n个不同重量不同价值的物品和一个容量一定的背包，设计方案使得在不超出背包容量的前提下，装进背包的物品总价值最高

（1）寻找动态规划函数

思路：
1、把物品进行编号，考虑物品编号从小到大依次放进包里，对每个物品是否放进包里分别做决策
2、每一次抉择并不一定是在以前的基础上继续放，有可能对之前的选择结果进行重组
比如：3个物品，重量分别是1,2,3，背包大小为5，前两个物品都放进去后，背包的空间大小只剩2，不足以放第3个物品。因此若经过衡量后，决定要将第3个物品放进去，包里必须至少拿出1个物品

• 定义递推量
  令C(i,j)表示前i个物品放到容量为j的背包里所创造的最大价值，则原问题的解是求C(n,W)，其中W为背包的容量。
• 定义其它变量
  wi——表示第i个物品的容量（Weight）
  vi——表示第i个物品的价值（value）

考虑一般情况：假如已经对前i-1个物品进行过抉择，现在抉择是否将第i个物品放进包里，需要考虑哪些问题？

1、第i个物品是否放得进包里

注意：这里是考察第i个物品是否能放得进背包里（包括空包），而不是在已有基础上放进去


若第i个物品的容量大于背包总容量，即wi>j，则前i个物品放到容量为j的包里的最大价值与前i-1个物品放到容量为j的包里的最大价值相等（因为第i个物品放不进去，没创造额外价值）

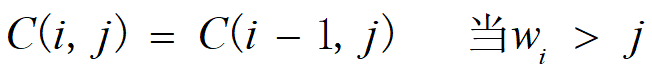
2、若第i个物品可以放进包里，放？不放？标准是什么？

• 2.1 若第i个物品可以放去背包里但选择不放，则与情况1相同，第i个物品没有创造价值，前i个物品的最大价值与前i-1个的最大价值相等，即
  
  
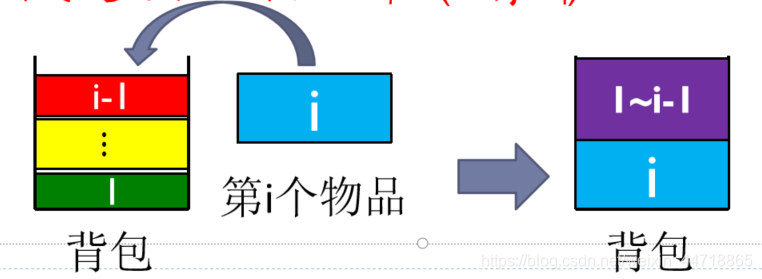
• 2.2 若第i个物品可以放进包里，并且考虑将第i个物品放进包里，会出现两种情况：
  ① 包足够大，可以在之前基础上再放入第i个物品，此时将第i个物品放进包里，创造的价值最大，即
  
  
  ② 包不够大，需要重新调整包物品的组合：
  先把第i个物品放入包里，则当前包里的价值为vi，剩余空间为j-wi
  
  背包的最大价值取决于在剩余的j-wi空间里放前i-1个物品所创造的最大价值，即C(i-1, j-wi)

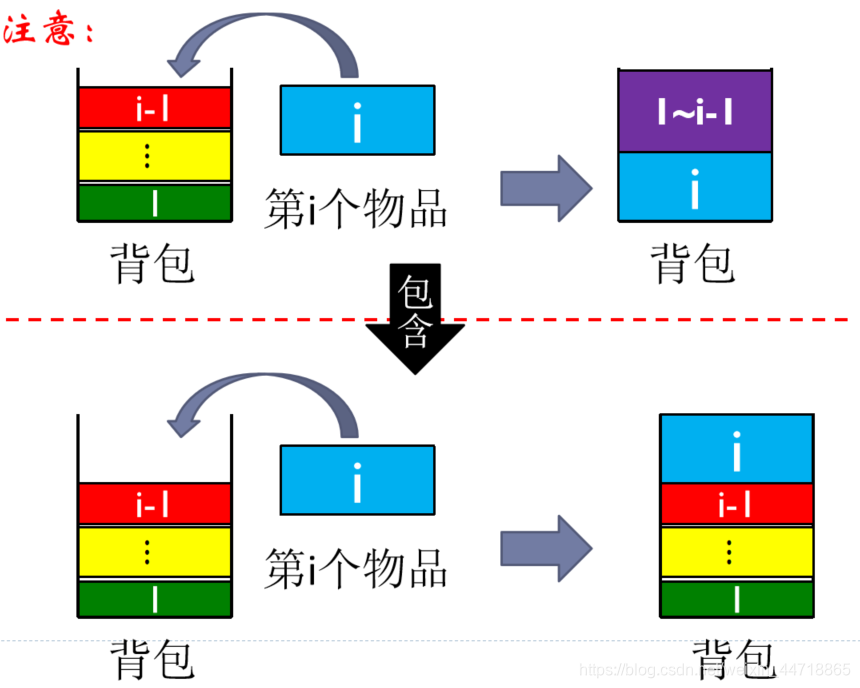
当第i个物品可以放进包里，前i个物品所创造的最大价值为：

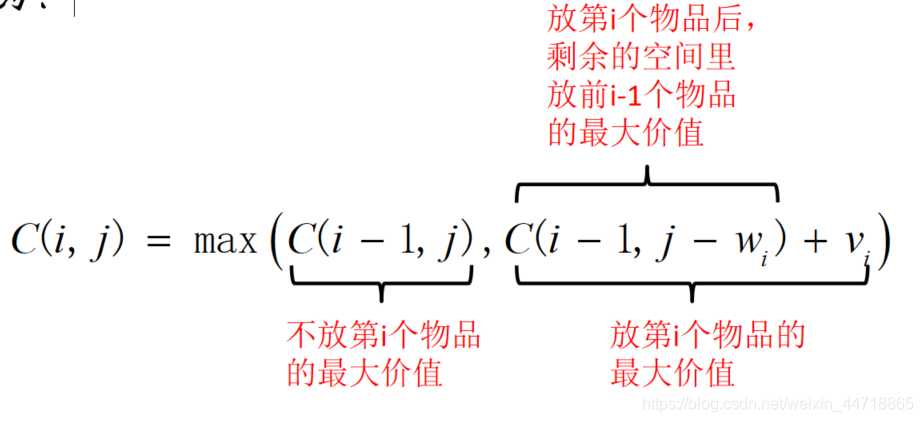
综上，0/1背包问题的动态函数如下：

（2）初始值

两个极端：
1、不往背包里放物品，即C(0, )，背包最大价值为0；
2、背包不能装任何东西，即C(, 0)，背包最大价值也是0。

（3）填表

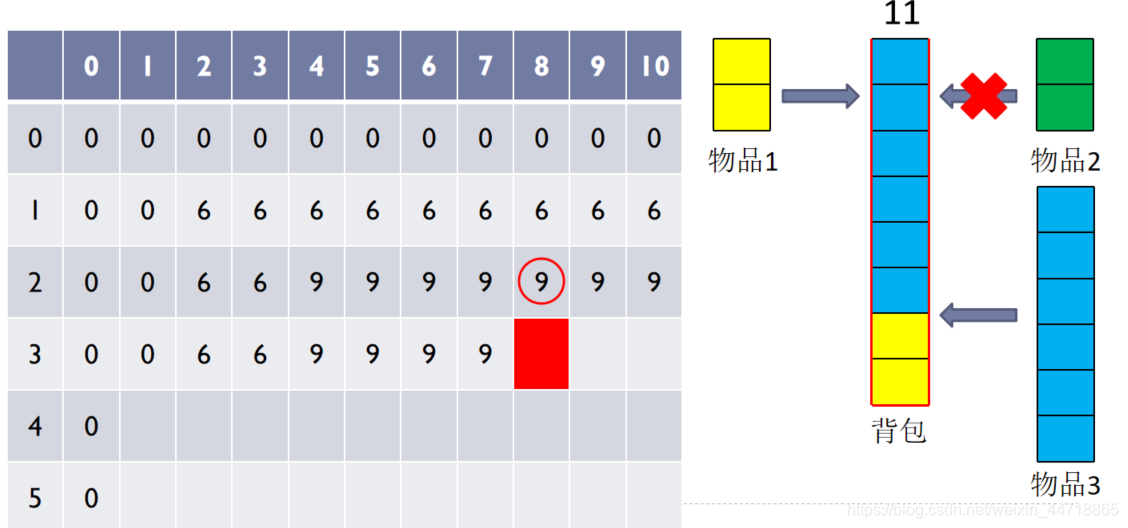
考虑5个物品，重量分别是{2, 2, 6, 5, 4}，价值分别为{6, 3, 5, 4, 6}，背包容量为10
步骤：
① 先填写初始解：C(i, 0)和C(0, j)
② 考虑C(1,1)，即把第1个物品放到容量为1的背包 →放不进C(1,1)=C(0,1)=0

③ 考虑C(1,2)，即把第1个物品放到容量为2的背包 →放得进

• 不放，则背包的最大价值为之前物品放到背包的最大价值，即C(1,2)=C(0,2)=0
  
• 放，则背包里的最大价值是之前物品放到2-w1=0空间里的最大价值加上物品1的价值，即C(1,2)=C(0,0)+v1=6
  
• C(1,2)的最大价值是上面两种价值的最大，即：C(1,2)=max(0,6)=6

考虑 C(2,2)的最大价值:由于j=2≥w2=2，第2个物品能放到包里，因此有以下两种情况：
① 不放第2个物品，此时背包最大价值是前1个物品放到背包里的最大价值，即C(2,2)=C(1,2)=6
② 放第2个物品，此时背包最大价值由前1个物品放到j-w2=0空间里的最大价值加上物品2的价值，即C(2,2)=C(1,0)+v2=3
相当于不放物品1，放物品2
因此，2个物品放到容量为2的背包的最大价值C(2,2)=max(3, 6)=6
也就是说，当背包空间只有2时，放物品1比物品2更有价值

考虑3个物品放到容量为8的背包所得到的最大价值，即C(3,8)
① 考察第3个物品能否放得进去：w3=6 < j=8
第3个物品能放进包，因此要讨论两种情况：放？不放？
② 第3个物品不放，则背包的最大价值为前2个物品放到背包的最大值，即：C(3,8)=C(2,8)=9

③ 第3个物品放到包里，则背包的最大价值为前2个物品放到j-w3=8-6=2空间里的最大值加上物品3的价值，即：
C(3,8)=C(2,2)+v3=6+5=11
相比第3个物品放(9)与不放(11)时的最大价值得出，放的价值更大

例题

题目：
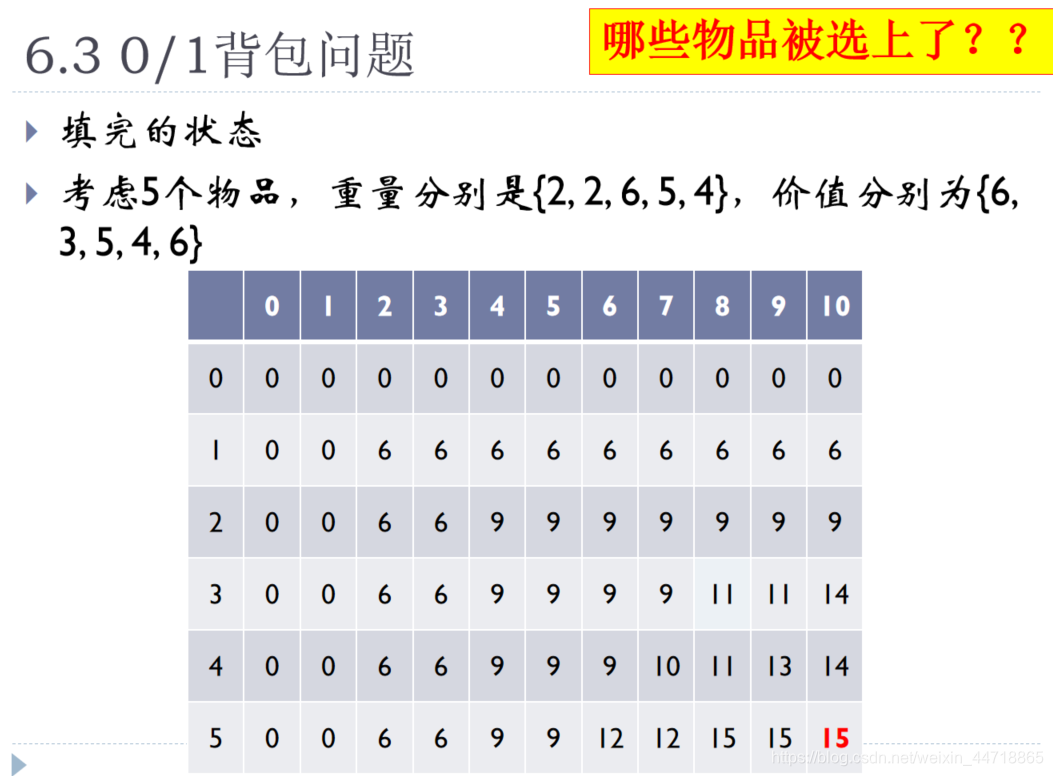
给定5个物品，其重量分别是（3,2,1,4,5），价值分别为（25,20,15,40,50），背包容量为6。用动态规划法求解该0/1背包问题的最优解，写出求解过程（列出动态规划函数、利用该函数填表，并指出最终解。）
解答过程：
1、初始值：c(i,0)和c(0,j)为0
2、C(1,1);把前一个放进容量为1的背包所得到的最大价值；C(1,1)=C(0,1)=0
3、C(1,2)；把前一个放进容量为2的背包所得到的最大价值；C(1,2)=C(0,2)=0;
4、C(1,3);把前一个放进容量为3的背包所得到的最大价值；C(1,3)=max(C(0,3),C(0,0)+25)=25
5、C(1,4);把前一个放进容量为4的背包所得到的最大价值;C(1,4)=max(C(0,4),C(0,1)+25)=25
6、C(1,5);把前一个放进容量为5的背包所得到的最大价值;C(1,5)=max(C(0,5),C(0,2)+25)=25
7、C(1,6);把前一个放进容量为6的背包所得到的最大价值;C(1,6)=max(C(0,6),C(0,3)+25)=25
8、C(2,1);把前二个放进容量为1的背包所得到的最大价值;C(2,1)=C(1,1)=0;
9、C(2,2);把前二个放进容量为2的背包所得到的最大价值;C(2,2)=max(C(1,2),C(1,0)+20)=20;
10、C(2,3);把前二个放进容量为3的背包所得到的最大价值;C(2,3)=max(C(1,3),C(1,1)+20)=25;
11、C(2,4);把前二个放进容量为4的背包所得到的最大价值;C(2,4)=max(C(1,4),C(1,2)+20)=25;
12、C(2,5);把前二个放进容量为5的背包所得到的最大价值;C(2,5)=max(C(1,5),C(1,3)+20=45;
13、C(2,6);把前二个放进容量为6的背包所得到的最大价值;C(2,6)=max(C(1,6),C(1,4)+20)=45;
14、C(3,1);把前三个放进容量为1的背包所得到的最大价值;C(3,1)=max(C(2,1),C(2,0)+15)=15;
15、C(3,2);把前三个放进容量为2的背包所得到的最大价值;C(3,2)=max(C(2,2),C(2,1)+15)=20;
16、C(3,3);把前三个放进容量为3的背包所得到的最大价值;C(3,3)=max(C(2,3),C(2,2)+15)=35;
17、C(3,4);把前三个放进容量为4的背包所得到的最大价值;C(3,4)=max(C(2,4),C(2,3)+15)=40;
18、C(3,5);把前三个放进容量为5的背所得到的最大价值;C(3,5)=max(C(2,5),C(2,4)+15)=45;
19、C(3,6);把前三个放进容量为6的背包所得到的最大价值;C(3,6)=max(C(2,6),C(2,5)+15=60;
20、C(4,1);把前四个放进容量为1的背包所得到的最大价值;C(4,1)=C(3,1)=15;
21、C(4,2);把前四个放进容量为2的背包所得到的最大价值;C(4,2)=C(3,2)=20;
22、C(4,3);把前四个放进容量为3的背包所得到的最大价值;C(4,3)=C(3,3)=35;
23、C(4,4);把前四个放进容量为4的背包所得到的最大价值;C(4,4)=max(C(3,4),C(3,0)+40)=40;
24、C(4,5);把前四个放进容量为5的背包所得到的最大价值;C(4,5)=max(C(3,5),C(3,1)+40)=55;
25、C(4,6);把前四个放进容量为6的背包所得到的最大价值;C(4,6)=max(C(3,6),C(3,2)+40)=60;
26、C(5,1);把前五个放进容量为1的背包所得到的最大价值;C(5,1)=C(4,1)=15;
27、C(5,2);把前五个放进容量为2的背包所得到的最大价值;C(5,2)=C(4,2)=20;
28、C(5,3);把前五个放进容量为3的背包所得到的最大价值;C(5,3)=C(4,3)=35;
29、C(5,4);把前五个放进容量为4的背包所得到的最大价值;C(5,4)=C(4,4)=40;
30、C(5,5);把前五个放进容量为5的背包所得到的最大价值;C(5,5)=max(C(4,5),C(4,0)+50)=55;
31、C(5,6);把前五个放进容量为6的背包所得到的最大价值;C(5,6)=max(C(4,6),C(4,1)+50)=65;

由上图可知编号为3,5两个物品被选上，总价值为65；
由第3个物品的重量为1，第5个物品的重量为5，所以背包为6的容量刚好装下。第3个物品的价值为15，第5个物品价值为50，两者价值加起来刚好为65；

6.4、组合问题

6.4.1、最长递增子序列

（1）寻找动态规划函数

定义递推量

L(i)，表示前i个数的子序列以第i个数结尾时的最长递增子序列长度。
比如：对于序列{5, 2, 8, 3, 1, 6, 9, 7}，L(3)表示子序列{5,2,8}的最长递增子序列长度2；L(5)表示{5,2,8,3,1}的最长递增子序列长度1(注意：不是2，因为必须以1结尾)

分析

• 对于序列{5, 2, 8, 3, 1, 6, 9, 7}，考虑前3个数构成的子序列{5, 2, 8}，其产生的递增子序列如下：
  （1）以5结尾的递增子序列为：{5}
  （2）以2结尾的递增子序列为：{2}
  （3）以8结尾的递增子序列为：{8},{5,8},{2,8}

L(3)表示以第3个元素(8)结尾的最长递增子序列长度，为2

• 考虑增加元素3到序列{5,2,8}末尾，则序列{5,2,8,3}构成的最长递增子序列长度是多少？
  ① 由于5>3，表明以5结尾的所有递增序列都不能与3构成更长的递增序列；
  ② 2<3，表明以2结尾的所有递增序列可以与3构成长度加1的递增序列。在前3个数中，以2结尾的递增子序列为{2}，长度为1，因此加入3后，递增子序列变为{2, 3}，长度为2。
  ③ 8的情况与5相同
  综上，加入3后，以3结尾的递增序列只有{2,3}，其长度为2，因此有L(4)=L(2)+1=2

• 考虑再增加元素1到序列{5,2,8,3}末尾，则分析序列{5,2,8,3,1}构成的最长递增子序列发现，1以前的所有元素都比1大，表明所有以这些元素结尾的递增序列都不能与1构成更长的递增序列。因此，加入1后，以1结尾的递增序列只有{1}，其长度为1，因此有L(5)=1

• 考虑再增加元素6到序列{5,2,8,3,1}末尾，则分析序列{5,2,8,3,1,6}构成的最长递增子序列：
  ① 5<6，表明以5结尾的所有递增序列可以与3构成长度加1的递增序列。以5结尾的递增子序列为{5}，长度为1，则加入6后，递增子序列变为{5,6}，长度为2；
  ② 2<6，表明以2结尾的所有递增序列可以与6构成长度加1的递增序列。以2结尾的递增子序列为{2}，长度为1，因此加入6后，递增子序列变为{2,6}，长度为2。
  ③ 8>6，表明以8结尾的所有递增序列都不能与6构成更长的递增序列
  ④ 3<6，表明以3结尾的所有递增序列可以与6构成长度加1的递增序列。以3结尾的递增子序列为{3}，{2,3},最长长度为2，则加入6后，递增子序列变为{3,6}和{2,3,6}，最长长度为3；
  ⑤ 1<6，表明以1结尾的所有递增序列可以与6构成长度加1的递增序列。以1结尾的递增子序列为{1}，长度为1，因此加入6后，递增子序列变为{1,6}，长度为2。
  综上，加入6后，能与其构成更长的递增子序列的是以5,2,3和1结尾的序列，构成的子序列分别为{5,6},{2,6},{2,3,6},{1,6}，最长长度为3，因此，L(6)=max(L(1)+1,L(2)+1,L(4)+1,L(5)+1)=3

考虑部分解L(i)的计算

假设序列(a1,a2,…,ai-1)以a1结尾的最长递增子序列长度为l1，以a2结尾的最长递增子序列长度为l2，…，以ai-1结尾的最长递增子序列长度为li-1，即L(i-1)=li-1

加入ai后，检查是否产生更长的递增子序列：让ai与前i-1个元素分别进行比较，出现两种情况：
① ai比前i-1个元素都小，不能与以任何元素结尾的序列构成更长的递增子序列，因此以ai结尾的递增子序列只有{ai}，长度为1，即L(i)=1，当不存在aj<ai, 0≤j<i
② ai比前i-1个元素的某些元素大，假如是ar,as,at，满足ar<ai, as<ai, at<ai，表明ai可以分别与以ar,as,at结尾的序列构成更长的递增子序列，因此以ai结尾的递增子序列有{_ar,ai}，{as,ai}, {~at,ai}，长度分别为lr+1，ls+1和lt+1。则以ai结尾的最长递增子序列应为上面3个长度最长的一个，即

（3）填表

考虑序列{5, 2, 8, 6, 3, 6, 9, 7}的最长递增子序列问题

① 填写初始解： i=1时，L(i)=1
② 计算L(2)：由于a1>a2，{a1,a2}不能构成递增子序列，因此，L(2)=1，单独为最长递增子序列
③ 计算L(3)：
a1<a3，构成递增子序列{5,8}，长度为2；
a2<a3，构成递增子序列{2,8}，长度为2；
因此，L(3)=max(2,2)=2，两个子序列均为当前最长
④ 计算L(6)：
a1<a6，构成递增子序列{5,6}，长度为2；
a2<a6，构成递增子序列{2,6}，长度为2；
a5<a6，构成递增子序列{2,3,6}，长度为3；
⑤ 填完表，L(8)即为序列最长递增子序列长度。
最长递增子序列有两个，分别是：{2,3,6,9}和{2,3,6,7}

时间复杂度分析

6.4.2、最长公共子序列

问题描述：
对于一个序列X=(x1,x2,…,xm)，其子序列是由X部分元素构成的序列，且满足以下两个条件：
① 子序列中的元素不一定是原序列的连续元素；
② 子序列各元素顺序必须与原序列相同
比如： X=(a,b,c,b,d,b), 其子序列可能是{a,c}, {b,c,d}, {a,b,b}，但不可以是{c,a}或者{d,c}

给定序列X=(x1,x2,…,xm)和序列Y=(y1,y2,…,yn)，若X和Y的某个子序列相同，则该子序列为X和Y的公共子序列，记为Z=(z1,z2,…,zk)。最长公共子序列问题即是找一个最长的Z

（1）寻找动态规划函数

定义递推量：

若X序列长m，Y序列长n，设L(i,j)表示X序列取0_{i-1，Y序列取0}j-1时其最长公共子序列的长度

研究部分解L(i,j)的计算

设当X长度为i，Y长度为j时，得到的最长公共子序列Z长度为k。考虑xi, yj和zk的关系：
① xi=yj，表明xi和yj是公共子序列的一个组成元素，此时有zk = xi = yj

比如：Xi = {a,a,b,a,c}, Yj = {a,c,a,b,c}，则最长公共子序列为Zk = {a,a,b,c}

将上述X，Y的子序列缩减，将最后一个元素移除

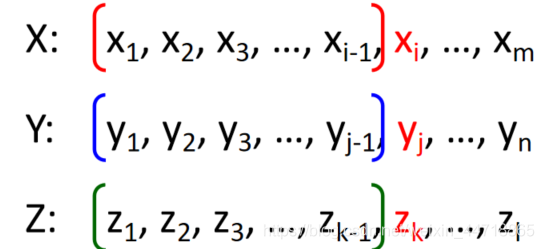
则上述i-1长的X序列和j-1长的Y序列，其公共子序列必然是k-1长的Z序列
注意：此处并不代表xi-1 = yj-1 = zk-1

比如：Xi = {a,a,b,a,c}, Yj = {a,c,a,b,c}，其最长公共子序列Zk = {a,a,b,c}；Xi-1 = {a,a,b,a}, Yj-1 = {a,c,a,b}，则最长公共子序列为 {a,a,b}
对比两个子序列的公共子序列长度关系






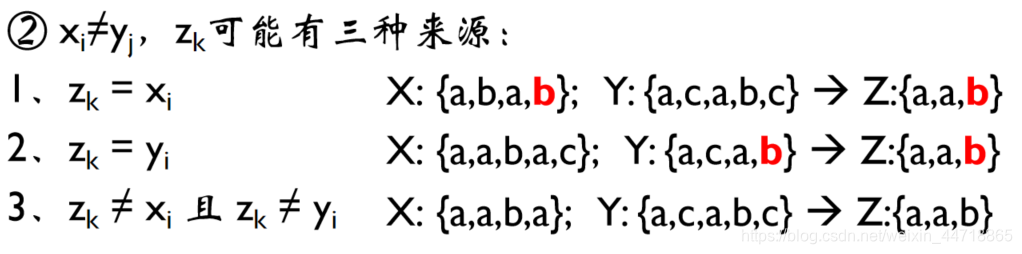
（2）初始值
当给定的X和Y序列是怎样时，其最长公共子序列的长度最容易算？
只有一个元素？
没有元素时最容易算？要算吗？

最长公共子序列的初始值是，当X或Y序列长度为0时，其公共子序列长度为0

从S(5,5)开始，由于S(5,5)=1，因此元素c为公共元素，记录并回溯S(4,4)
S(4,4)=3，缩减X序列，搜索下一个位置：S(3,4)
S(3,4)=1，因此元素b为公共元素，记录并回溯S(2,3)
S(2,3)=1，因此元素a为公共元素，记录并回溯S(1,2)
S(1,2)=2，缩减Y序列，搜索下一个位置：S(1,1)
S(1,1)=1，因此元素a为公共元素，记录并回溯S(0,0)

当回溯至i或j为0时，回溯结束，回溯过程中记录下来的元素（倒过来）即为最长的公共子序列，即

算法分析

例题

假设两个字符串X和Y，X=“abcabac”，Y=“acabcac”。采用动态规划法求X和Y的最长公共子序列。请先列出其动态规划函数，指出初始值，并通过填表来求解该问题，最后给出问题的结论，即最长公共子序列是什么，其长度为多少

（1）动态规划函数：

（2）初始值

L(i,0)=0; L(0,j)=0; S(i,0)=0; S(0,j)=0

（3）填表

L(1,1)=L(0,0)+1=1; S(1,1)=1;
L(1,2)=max(L(1,1),L(0,2))=1; S(1,2)=2;
L(1,3)=L(0,2)=1; S(1,3)=1;
L(1,4)=max(L(1,3),L(0,4))=1; S(1,4)=2;
L(1,5)=max(L(1,4),L(0,5))=1; S(1,5)=2;
L(1,6)=L(0,6)+1=1; S(1,6)=1;
L(1,7)=max(L(1,6),L(0,7))=1; S(1,7)=2;
L(2,1)=max(L(2,0),L(1,1))=1; S(2,1)=3;
L(2,2)=max(L(2,1),L(1,2))=1; S(2,2)=2;
L(2,3)=max(L(2,2),L(1,3))=1; S(2,3)=2;
L(2,4)=L(1,3)+1=2; S(2,4)=1;
L(2,5)=max(L(2,4),L(1,5))=2; S(2,5)=2;
L(2,6)=max(L(2,5),L(1,6))=2; S(2,6)=2;
L(2,7)=max(L(2,6),L(1,7))=2; S(2,7)=2;
L(3,1)=max(L(3,0),L(2,1))=1; S(3,1)=3;
L(3,2)=L(2,1)+1=2; S(3,2)=1;
L(3,3)=max(L(3,2),L(2,3))=2; S(3,3)=2;
L(3,4)=max(L(3,3),L(2,4))=2; S(3,4)=2;
L(3,5)=L(2,4)+1=3; S(3,5)=1;
L(3,6)=max(L(3,5),L(2,6))=3; S(3,6)=2;
L(3,7)=L(2,6)+1=3; S(3,7)=1;
L(4,1)=L(3,0)+1=1; S(4,1)=1;
(4,2)=max(L(4,1),L(3,2))=2; S(4,2)=3;
L(4,3)=L(3,2)+1=3; S(4,3)=1;
L(4,4)=max(L(4,3),L(3,4))=3; S(4,4)=2;
L(4,5)=max(L(4,4),L(3,5))=3; S(4,5)=2;
L(4,6)=L(3,5)+1=4; S(4,6)=1;
L(4,7)=max(L(4,6),L(3,7))=4; S(4,7)=2;
L(5,1)=max(L(5,0),L(4,1))=1; S(5,1)=3;
L(5,2)=max(L(5,1),L(4,2))=2; S(5,2)=3;
L(5,3)=max(L(5,2),L(4,3))=3; S(5,3)=3;
L(5,4)=L(4,3)+1=4; S(5,4)=1;
L(5,5)=max(L(5,4),L(4,5))=4; S(5,5)=2;
L(5,6)=max(L(5,5),L(4,6))=4; S(5,6)=2;
L(5,7)=max(L(5,6),L(4,7))=4; S(5,7)=2;
L(6,1)=L(5,0)+1=1; S(6,1)=1;
L(6,2)=max(L(6,1),L(5,2))=2; S(6,2)=3
L(6,3)=L(5,2)+1=3; S(6,3)=1;
L(6,4)=max(L(6,3),L(5,4))=4; S(6,4)=3;
L(6,5)=max(L(6,4),L(5,5))=4; S(6,5)=2;
L(6,6)=L(5,5)+1=5; S(6,6)=1;
L(6,7)=max(L(6,6),L(5,7))=5; S(6,7)=2;
L(7,1)=max(L(7,0),L(6,1))=1; S(7,1)=3;
L(7,2)=L(6,1)+1=2; S(7,2)=1;
L(7,3)=max(L(7,2),L(6,3))=3; S(7,3)=3;
L(7,4)=max(L(7,3),L(6,4))=4; S(7,4)=3;
L(7,5)=L(6,4)+1=5; S(7,5)=1;
L(7,6)=max(L(7,5),L(6,6))=5; S(7,6)=2;
L(7,7)=L(6,6)+1=6; S(7,7)=1;

（5）回溯

由填表得最长公共子序列长度为6；
S=1 →S(i-1,j-1) S=2 →S(i,j-1) S=3 →S(i-1,j)
从S(7,7)开始，S(7,7)=1;因此c是公共元素，记录并回溯到S(6,6);
S(6,6)=1;因此a是公共元素,记录并回溯到S(5,5);
S(5,5)=2;缩减Y序列，搜索下一个位置：S(5,4);
S(5,4)=1;因此b是公共元素,记录并回溯到S(4,3);
S(4,3)=1;因此a是公共元素,记录并回溯到S(3,2);
S(3,2)=1,因此c是公共元素,记录并回溯到S(2,1);
S(2,1)=3,缩减X序列，搜索下一个位置:S(1,1);
S(1,1)=1,因此a是公共元素,记录并回溯到S(0,0);
所以X,Y的最长的公共子序列Z={a,c,a,b,a,c}；
所以X,Y的最长的公共子序列的长度为6；

6.5、多段图的最短路径问题

什么是多段图？
（1）是一个带权有向图
（2）可以将结点划分成若干堆（段），而且图中任何一边连接的两个结点不会在同一段中

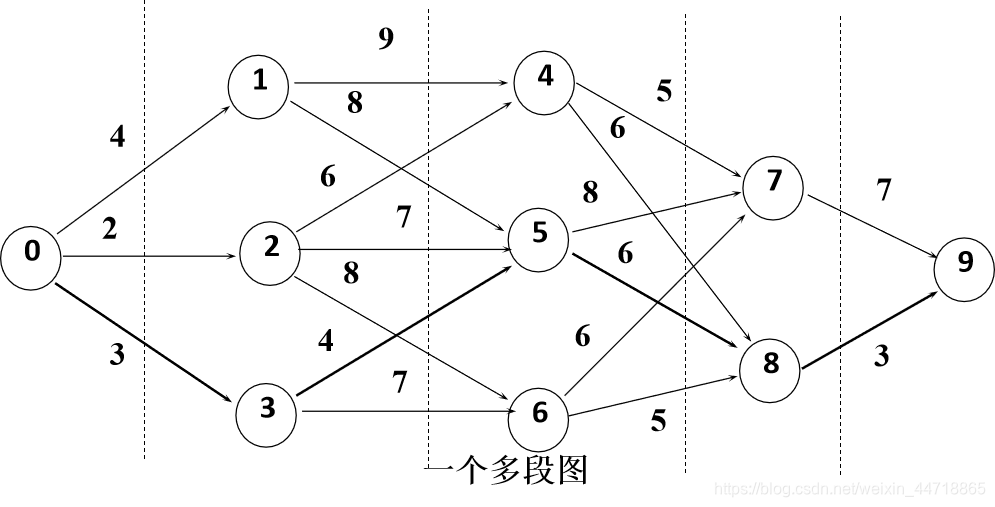
编号：按段从左到右编排，在同一段的结点互不相连
多段图的最短路径问题是求0号结点到n号结点的最短路径

（1）寻找动态规划函数
定义d(i,j)表示从第i个结点到第j个结点的最短路径，ci,j表示第i个结点和第j个结点的距离。研究部分解d(0,j)的计算

分析：要从0点出发到达j点，只能有三种途径：1)从0点先到v1点，再到j；2)从0先到v2点，再到j；3)从0点先到v3点，再到到j。哪条路最短？
① 从0出发先到v1点，再到j点的路径，其长度应为0到v1点的最短路径长度加上v1到j点的长度，即
d(0, j)v1 = d(0,v1) + cv1,j

② 同理，从0出发通过v2点到达j点，其最短路径长度为
d(0, j)v2 = d(0,v2) + cv2,j

③ 从0出发经过v3点到达j点的最短路径长度为：
d(0, j)v3 = d(0,v3) + cv3,j

分析：从0到j只有该3条路径，因此其最短路径长度应为3条路径中最短的一条，即d(0,j) = min(d(0,s)+cs,j)
s是与j存在有向边<s,j>的点(v1, v2, v3)

（2）初始值：从0点出发不经过任何中间结点能到达的顶点(0→v1,0→v2,0→v3)，其路径长度为：
d(0,v1) = c0,v1, d(0,v2) = c0,v2, d(0,v3) = c0,v3,

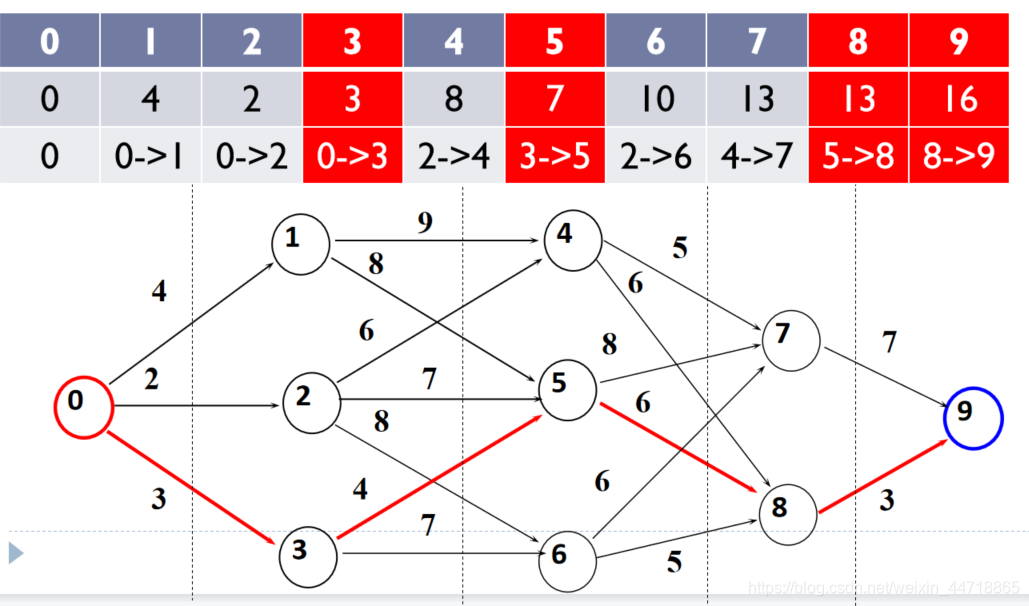
（3）填表：
① 初始化

② 0→4的最短路径为min(0→1+9,0→2+6)=8

③ 0→5的最短路径为min(0→1+8,0→2+7,0→3+4)=7

④ 依次将表填完，得到09的最短路径长度为16

（4）回溯：
从最后结点回溯最短路径

算法分析

算法分析（思路）：
（1）填表过程是先填0到1点，然后填0到2点，一直到0到n点，共n次。
（2）要计算0点到第j个点的最短路径长度，需要分别计算j点的各入度边的路径长度，而且每条入度边在整个计算过程中只计算一次。因此，假设图中边数为m，计算这n次填充需要计算的次数为m。
（3）回溯输出路径：与图划分得到的段数k有关

因此，总的计算量为：

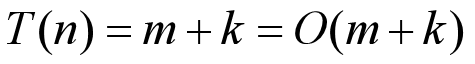
算法分析（程序实现）：
（1）填表过程是先填0到1点，然后填0到2点，一直到0到n点，共n次。
（2）要计算0点到第j个点的最短路径长度，需要分别比较0到前j-1个点加上各点到j点的路径长度，因此需要j-1次比较；
（3）回溯输出路径：与图划分得到的段数k有关
因此，总的计算量为：

例题

求以下多段图的最短路径，写出求解过程

解：
（1）最短路径长度计算：d(1,j)=min(d(1,s)+Cs,j)
（2）初始值：从1点发不经过任何中间结点能到达的顶点（1V2,1V3,1V4）
其路径长度为：
d（1，V2）=C1,v2，d（1，V3）=C1,v3，d（1，V4）=C1,v4
（3）填表
1、初始化
2、15的最短路径为min（12+13,13+6）=14
3、16的最短路径为min（12+3,14+7）=6
4、17的最短路径为min（13+5,14+4）=9
5、18的最短路径为min（15+4,16+3）=9
6、19的最短路径为min（16+3,17+8）=9
7、110的最短路径为min（18+7,19+9）=16
（4）回溯

从最后结点回溯最短路径为：126810
最短路径长度为：16

7、贪心算法

7.1、基本思想：

按照某种策略顺序，依次选择使问题达到最优的解

特点：
（1）常用于求最优问题；
（2）一旦选定，求解过程中不再改变；
（3）通常得到的解为局部最优解。

采用贪心法的一般步骤：
（1）按照策略要求对数据进行排序
（2）依次选择问题的解

埃及分数问题
问题描述： 用最少的且分子为1的分数来表示真分数
比如：

想法： 将真分数依次与1/2, 1/3, 1/4…比较，将第一个大于该真分数的分数作为埃及分数，并令真分数减去该埃及分数。将减后的结果继续比较，直到余值就是一个埃及分数。

• 假设真分数由A/B表示，由于A<B，令B/A的整数部分为C，余数部分为D，即：B = A × C + D
• 两边同时除以A，得：B/A = C + D/A < C + 1
• 两边同时取倒数，得：A/B > 1 / (C + 1)
• 令E = C + 1，则1/E为A/B的一个埃及分数。
• 考虑余数：A/B - 1/E = ((A × E) – B) / (B × E)；因此，新的A和B为：A = (A × E) – B；B = B × E
• 考虑到上式的A和B可能在公因子，因此需要除以两者最大公约数，即A = A / R；B = B / R；其中，R为A和B的最大公约数

7.2、TSP问题

问题描述：从某个城市出发，遍历其余城市一次再回到出发城市，要求路程最短

贪心策略：
（1）最近邻点策略：从某个城市出发，依次选择与当前结点相邻且不为出发点的权重最小的点，将最后一点跟出发点相连，构成回路
（2）最短链接策略：从相邻边中选择权重最小的边，构成路径的一部分



最近邻点策略的时间复杂度：
（1）需要依次选取n-1个结点
（2）确定第i个结点，需要扫描剩余的n-i个结点，选择与第i个结点相邻且权重最小的结点
因此时间复杂度为O(n2)
由于最后一个结点与起点的连线无法抉择，若该连线的权重很大，该方法也只能接受这条路径

（2）最短链接策略：从相邻边中选择权重最小的边，构成路径的一部分。被先中的边应满足三个条件：
选中边加到路径中不会构成回路
选中边加到路径中不会出现分枝

• 选择第1条权重最小的边
• 选择第2条权重最小的边
• 选择第3条权重最小的边
• 选择第5条权重最小的边
  
  
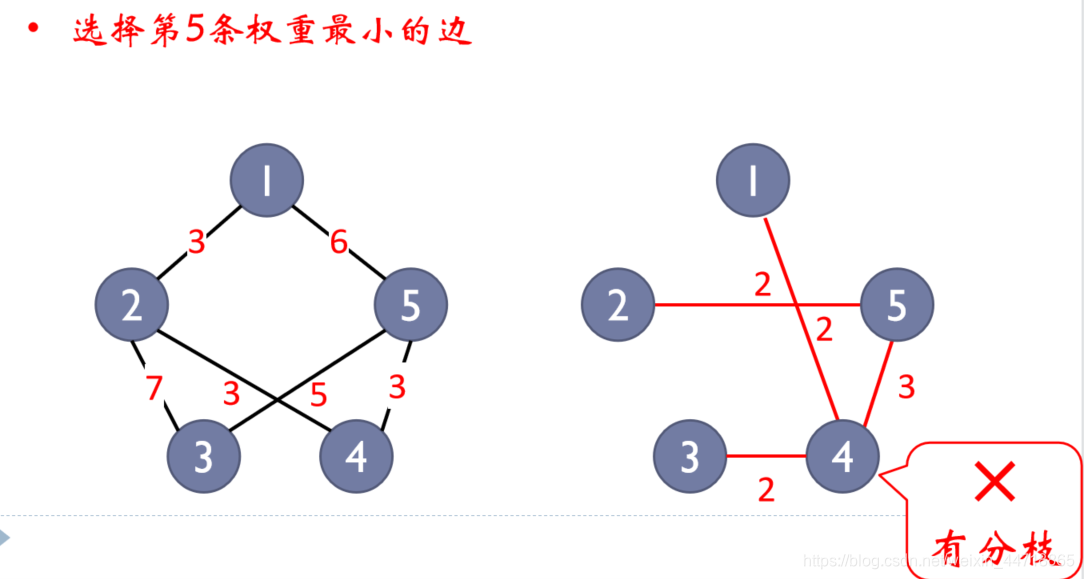
• 选择第6条权重最小的边
  
  算法分析：

（1）需要依次选取n-1条边
（2）确定第i条边时，需要扫描剩余的n-i条边，取权重最小，且不会出现回路或分枝的边
因此时间复杂度为O(n2)
若采用堆排序对边进行排序，则选取最短边的时间降为O(log2n)，因此时间复杂度为O(nlog2n)

贪心算法求解TSP问题时，有可能无解

例题

1、给定真分数19/29，用贪心算法求解其埃及分数问题。要求写出求解每一个埃及分数的步骤
答：
①A=19,B=29,A<B,令B/A的整数部分为C=1，余数为D=10，即B=AC+D，则29=191+10
两边同时除以A，得：B/A = C + D/A < C + 1即是29/19=1+10/19<1+1;
两边同时取倒数，得：A/B > 1 / (C + 1)即19/29>1/2；令E=C+1=2，则1/2为A/B的埃及分数。
②考虑余数A/B - 1/E = ((A × E) – B) / (B × E)即19/29-1/2=（（192）-29）/（292）
因此，新的A和B为：A = (A × E) – B=9；B = B × E=58；C=6；D=4;即B=AC+D，则58=96+4
两边同时除以A，得：B/A = C + D/A < C + 1即是58/9=6+4/9<6+1;
两边同时取倒数，得：A/B > 1 / (C + 1)即9/58>1/7；令E=C+1=6+1=7，则1/7为A/B的埃及分数。
③考虑余数A/B - 1/E = ((A × E) – B) / (B × E)即9/58-1/7=（（97）-58）/（587）
因此，新的A和B为：A = (A × E) – B=5；B = B × E=406；C=81；D=1;即B=AC+D，则406=581+1；
两边同时除以A，得：B/A = C + D/A < C + 1即是406/5=81+1/5<81+1;
两边同时取倒数，得：A/B > 1 / (C + 1)即5/406>1/82；令E=C+1=81+1=82，则1/82为A/B的埃及分数。
④考虑余数A/B - 1/E = ((A × E) – B) / (B × E)即
5/406-1/82=（（582）-406）/（40682）=4/33292=1/8323;所以余数1/8323为A/B的埃及分数
所以真分数19/29的埃及分数为：1/2,1/7,1/82,1/8323;

2、给定一个带权有向图如下，现以结点A为出发点，分别采用贪心法中的最近邻点策略和最短链接策略求解其TSP路径。要求画出每个步骤，并最终指出TSP路径是什么，长度是多少

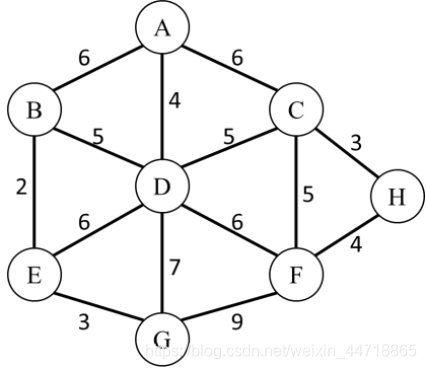
答：（1）最近邻点策略：

TSP路径为：ADCHFGEBA
路径长度为：36

（2）最短链接策略：

TSP路径为：ACHFGEBDA
路径长度为36

7.3、图着色问题

问题描述： 给定一个无向连通图G，对图中的各结点分别着色，要求相邻的结点颜色不能相同。图着色问题要求解出一种着色方案，使得在满足上述条件的情况下，所需要的颜色种类最少

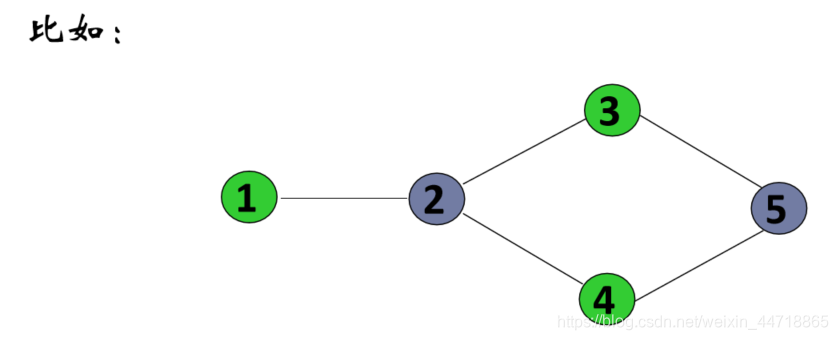
想法
（1）每一趟用一种颜色去着色，尽可能多地对结点进行着色
（2）按结点编号依次检查每一个结点，若该结点未被着色，且与该结点相邻的所有结点未被着色，或与当前颜色不同，则使用当前颜色对该结点进行着色。
（3）重复第（2）步直到所有结点均被着色

① 当前颜色为红色，检查结点1，发现与结点1相连的其它结点(4,6,8)均为被着色，因此结点1可着成红色

② 检查结点2，发现与结点2相连的其它结点(3,5,7)均为被着色，因此结点2可着成红色

③ 检查结点3，发现与结点3相连的其它结点(2,6,8)中，结点2已被着为红色，因此结点3不能着成红色

④ 同理，结点5和结点7因为与结点2相连，所以均不能着成红色；结点4,6和8与结点1相连，也不能着成红色。因此红色只能着结点1和结点2

⑤ 选择当前颜色为蓝色，检查结点1和结点2，发现两个结点均已着色，检查下一个结点
⑥ 检查结点3，发现与结点3相连的其它结点(2,6,8)中，结点2被着为红色，结点6和结点8未被着色，因此结点3可以被着成蓝色

⑦ 检查结点4，发现与结点4相连的其它结点(1,5,7)中，结点1被着为红色，结点5和结点7未被着色，因此结点4可以被着成蓝色

⑧ 依此算法，最后的着色方案如下，共用4种颜色：

不是最优解

上下两行分别着不同的颜色，只需要两种颜色：

最优解与结点编号顺序有关
若图的编号调整一下，可以用贪心法得到最优解：

算法分析：

假设图中结点数为n，需要的颜色种数为k。

对于每一种颜色(1~k)，都分别检查n个结点在着该颜色时是否发生冲突

因此，完成所有结点的着色的时间复杂度为O(k*n)

例题

对如下图所示无向图，写出使用贪心法对顶点着色的过程

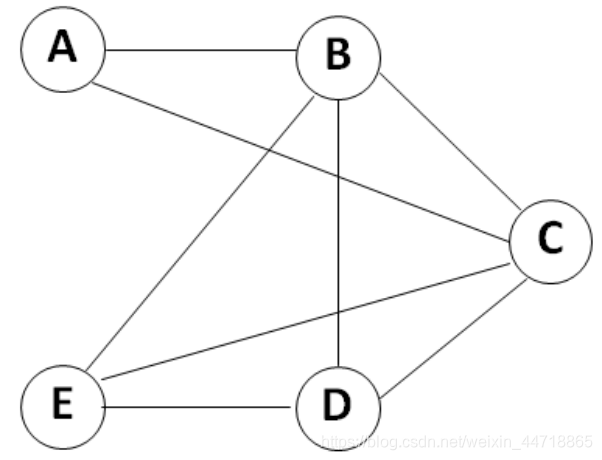
解：按ABCDE的顺序依次着色
（1）用颜色1着色：
a)A着颜色1，无冲突
b)B，C着颜色1，与A冲突
c)D着颜色1，无冲突
d)E着颜色1，与D冲突
（2）用颜色2着色：
a)A，D已着色
b)B着颜色2，无冲突
c)C，E着颜色2，与B冲突
（3）用颜色3着色：
a)A，B，D已 着色
b)C着颜色3，无冲突
c)E着颜色3，与C冲突
（4）E用颜色4着色
综上可得，完成着色需要4种颜色，各结点着色情况如下：
A，D着颜色1；B着颜色2；C着颜色3；E着颜色4

7.4、最小生成数问题

问题描述： 在一个带权无向图中，生成一棵总权重最小的树

贪心法策略
（1）Prim算法（最近顶点策略）

• 设定选定区和未选定区，初始状态，选定区只有起点
• 检查与选定区各结点相邻的结点，选择一个权重最小的结点来扩展生成树，直到所有结点被选过一次
  Prim算法分析：
  时间复杂度O(n2)
  与边无关，只与结点有关，适合用于稠密图（很多边的图）
  （2）Kruscal算法（最短边策略）
  不管起止点，每次选择权重最小且不会产生回路的边作为最小生成树的边，直到所有结点都被连接
  ① 选择第1条权重最小的边
  ② 选择第2条权重最小的边
  ③ 选择第3条权重最小的边
  ④ 选择第4条权重最小的边
  ⑤ 选择第5条权重最小的边
  
  
  时间复杂度O(nlog2n)
  与点无关，只与边有关，适合用于稀疏图（边较少的图）

例题

给定网络如下，分别用Prim算法和Kruscal算法求其最小生成树。要求详细写出求解过程

（1）Prim算法（以A为种子点）

最小权重为36
（2）Kruscal算法

最小权重为36

7.5、组合问题

7.5.1、背包问题

背包问题 VS 0/1背包问题

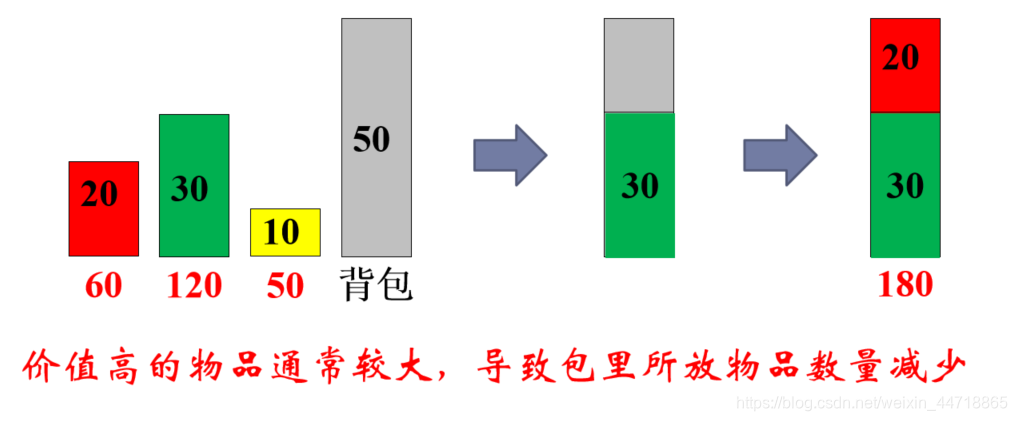
考虑下面的背包问题：有3个物品，其重量分别是{20, 30, 10}，价值分别为{60, 120, 50}，背包的容量为50

（1）贪心想法1：
先放价值最高的物品  包里装的物品都是比较有价值的

（2）贪心想法2：
先放容量最小的物品  包里装的物品最多

（3）贪心想法3：
先放单位价值最高的物品  价值最高

若用贪心法求0/1背包问题
（1）策略1

（2）策略2

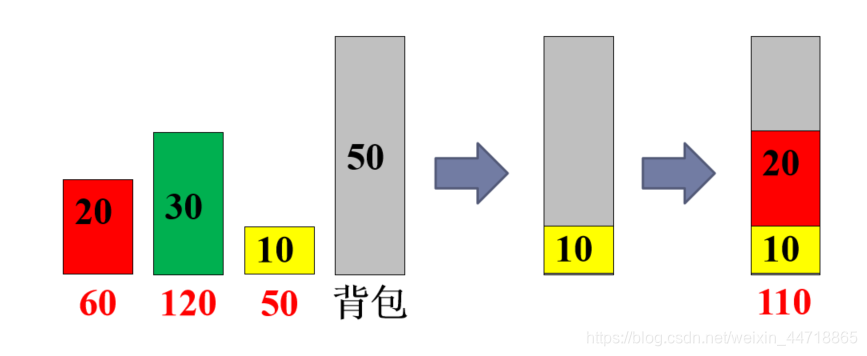
（3）策略3

算法分析：
贪心法实现前，需要对数据按某个特性排序。

• 对于背包问题中的策略1（优先选价值最高的），需要先对物品按价值从高到低排序；
• 对于策略2（优先选容量最小的），需要先对物品按容量从小到大排序；
• 对于策略3（优先选单位价值最高的），需要先对物品的单位价值从大到小排序。

因此主要时间复杂度在排序上，最快为O(nlog2n)

7.5.2、活动安排问题

问题描述：
设有n个活动E={1,2,…,n}，每个活动满足以下要求：
（1）每个活动都要求使用同一资源，而且同一时间内只有一个活动能使用这一资源
（2）每个活动都有一个开始时间si和结束时间fi，即活动在[si,fi)时间内进行

给定n个活动和每个活动的起止时间，活动安排问题是在时间不冲突的情况下，从这n个活动中安排尽可能多的活动来举办

7.5.3、多机调试问题