7.3(动态规划，518零钱兑换II，322. 零钱兑换）

518零钱兑换II

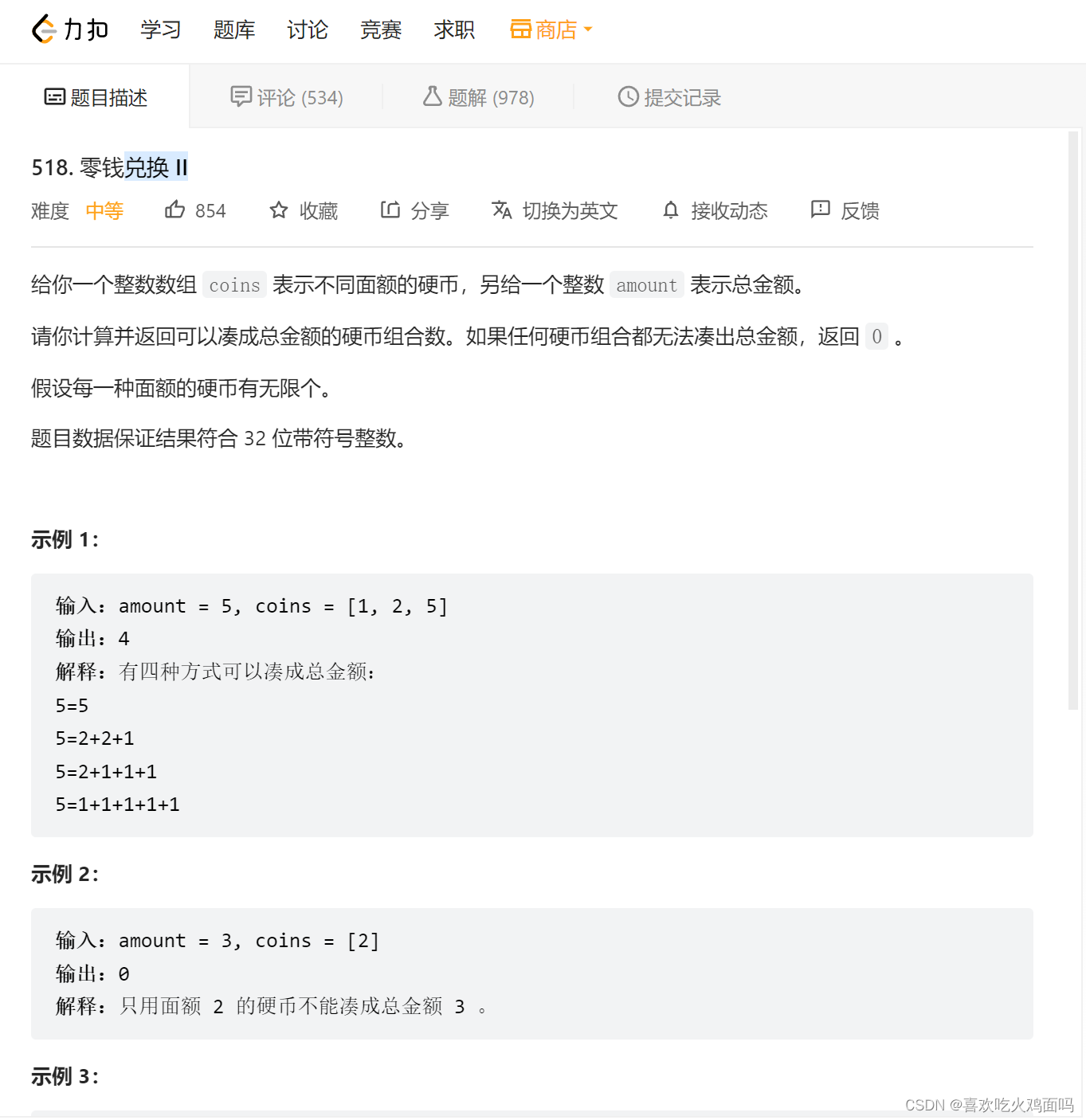
这道题目困扰了我一天了，我循序渐进做一下这道题目，这道题目是一个完全背包问题。先从最原始的方法讲起。也是复杂度最高的做法，枚举第i个物品选择0个，1个，2个一直到k个等等。我们从初始化讲起，dp[0][0] = 1表示的含义是，不选任何面值的硬币从而凑成价值为0的方法有一种。

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int n = coins.size();
        //一看先是一个背包问题，然后银币的总数可以选无限个，则是完全背包问题
        //设置dp数组，然后明确dp数组的含义
        vector<vector<int>> dp(coins.size()+1, vector<int>(amount+1, 0));
        //dp数组的含义就是，dp[i][j]从coins[0-i]中选可以填满背包容量为j的数组
        //有多少种方法
        
        //从前0个数中选，填满背包容量为0的背包

        dp[0][0] = 1;
        //先初始化，初始化是二维的难点
        
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
               for(int k = 0; k*coins[i-1]<=j; k++){
                   dp[i][j] = dp[i][j]+dp[i-1][j-k*coins[i-1]];
               }
            }
        }

        return dp[coins.size()][amount];
    }
};

然后进行优化，优化的方式也是数学证明版的优化。

所以对于此题，dp[i][j] = dp[i-1][j]+dp[i][j-coins[i-1]]。在这里我要解答一个我自己疑惑了一上午的问题，为什么我取第i个硬币，要用coins[i-1]，大家仔细看我们定义coins[0][j]是一个不取的情况，以此类推，coins[1][j]就是取coins集合中的头一个元素，也就是coins[0]。所以coins[i-1]就是按序取。这也困扰了我许久。自从得到这个优化方程了以后，我们可以将题目优化为二重循环。

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int n = coins.size();
        //一看先是一个背包问题，然后银币的总数可以选无限个，则是完全背包问题
        //设置dp数组，然后明确dp数组的含义
        vector<vector<int>> dp(coins.size()+1, vector<int>(amount+1, 0));
        //dp数组的含义就是，dp[i][j]从coins[0-i]中选可以填满背包容量为j的数组
        //有多少种方法
        
        //从前0个数中选，填满背包容量为0的背包

        dp[0][0] = 1;
        //先初始化，初始化是二维的难点
        
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
               if(j >= coins[i-1]) dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]];
               else dp[i][j] = dp[i-1][j];
            }
        }

        return dp[coins.size()][amount];
    }
};

然后就是将二维的问题像01背包那样优化到一维问题，这时候我们来注意一下状态转移方程
dp[i][j] = dp[i-1][j]+dp[i][j-coins[i-1]]。这个状态转移方程跟01背包就有所不同，dp[i-1]是来自上一行，dp[i][j-coins[i-1]]是来自本行，状态是已经被计算过了,所以在遍历背包容量时候，是从小往大遍历

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int n = coins.size();
        //一看先是一个背包问题，然后银币的总数可以选无限个，则是完全背包问题
        //设置dp数组，然后明确dp数组的含义
        vector<int> dp(amount+1, 0);
        //dp数组的含义就是，dp[i][j]从coins[0-i]中选可以填满背包容量为j的数组
        //有多少种方法
        
        //从前0个数中选，填满背包容量为0的背包
        dp[0] = 1;//只有一种方法，就是啥都不选
        
        
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
               if(j >= coins[i-1]) dp[j] = dp[j]+dp[j-coins[i-1]];
            }
        }

        return dp[amount];
    }
};

这就是一整天的成果了，还是可以的。给大家推荐一个可以听的明白的leecode讲解多重背包问题

322. 零钱兑换

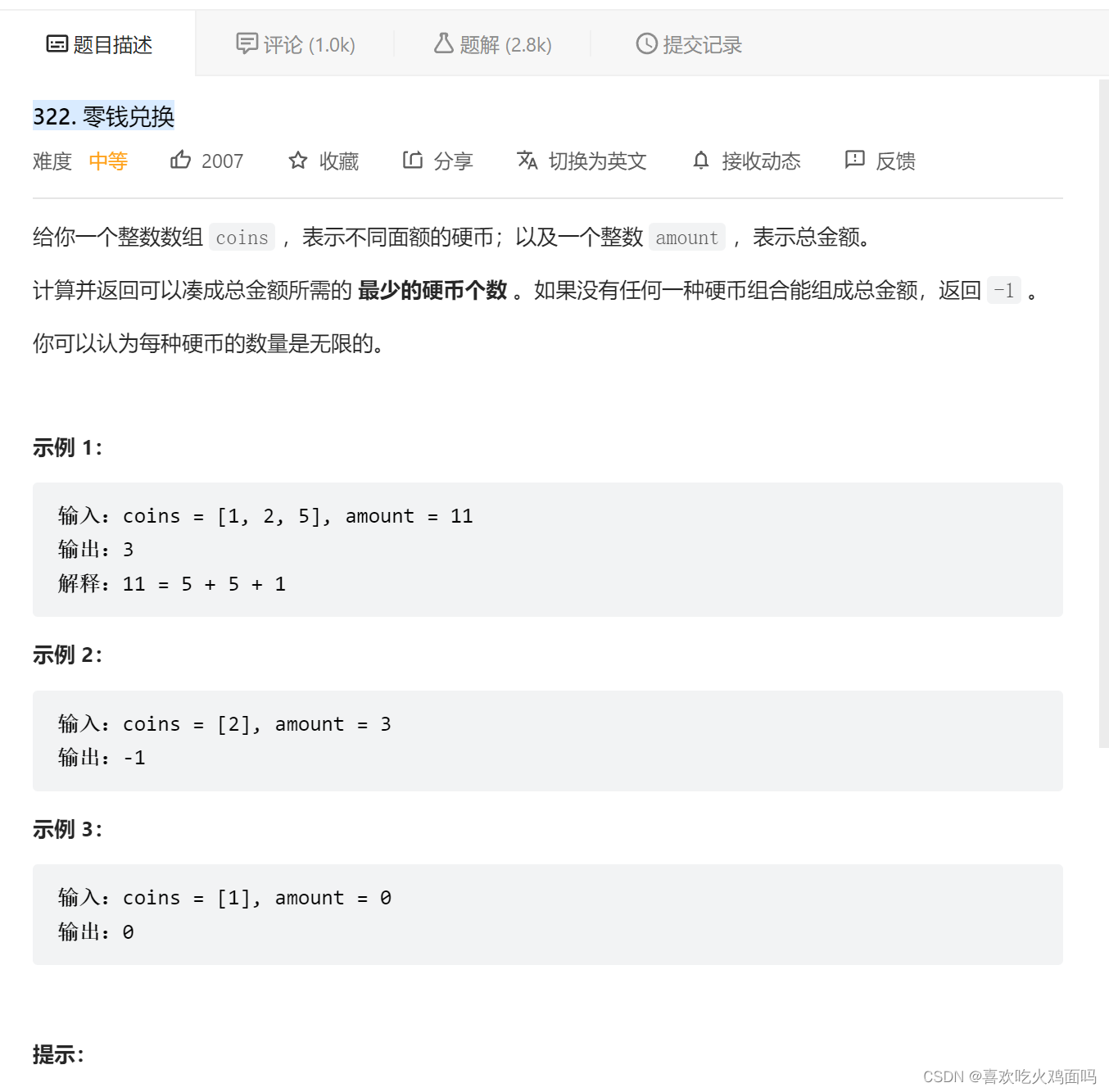
这道题目我们也是先从二维三重循环入手，代码如下。代码可以过，但是在leecode上超时了。。。

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //这道题目也是一道完全背包问题，分三步走做这道题
        //因为本题还不太一样，本题是求凑成amount所需最少的硬币个数
        //首先，明确dp数组的含义，d[i][j]表示从前i个物品中选择，能凑成j的最小的硬币的个数
        //最多的硬币个数是amount
        vector<vector<int>> dp(coins.size()+1, vector<int>(amount+1, amount+1));
        //从0种硬币中选择组成金额为0的硬币个数为0
        dp[0][0] = 0;
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
                for(int k = 0; k*coins[i-1]<=j; k++){
                    dp[i][j] = min(dp[i][j], dp[i-1][j-k*coins[i-1]]+k);//这里+k是因为我们需要用k个第i个硬币
                }
            }
        }

        //因为跟第一题目不同，这里还需要判断一下
        
        int ans = dp[coins.size()][amount];
        if(ans == amount+1) return -1;
        else return ans;
        
    }
};

然后让我们使用多重背包的方式优化一下

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //这道题目也是一道完全背包问题，分三步走做这道题
        //因为本题还不太一样，本题是求凑成amount所需最少的硬币个数
        //首先，明确dp数组的含义，d[i][j]表示从前i个物品中选择，能凑成j的最小的硬币的个数
        //最多的硬币个数是amount
        vector<vector<int>> dp(coins.size()+1, vector<int>(amount+1, amount+1));
        //从0种硬币中选择组成金额为0的硬币个数为0
        dp[0][0] = 0;
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
                if(j >= coins[i-1]) dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]]+1);//这里注意，+1
                else dp[i][j] = dp[i-1][j];
            }
        }

        //因为跟第一题目不同，这里还需要判断一下
        
        int ans = dp[coins.size()][amount];
        if(ans == amount+1) return -1;
        else return ans;
        
    }
};

然后用滚动数组优化

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //这道题目也是一道完全背包问题，分三步走做这道题
        //因为本题还不太一样，本题是求凑成amount所需最少的硬币个数
        //首先，明确dp数组的含义，d[i][j]表示从前i个物品中选择，能凑成j的最小的硬币的个数
        //最多的硬币个数是amount
        vector<int> dp(amount+1, amount+1);
        //从0种硬币中选择组成金额为0的硬币个数为0
        dp[0] = 0;
        for(int i = 1; i <= coins.size(); i++){
            for(int j = 0; j <= amount; j++){
                if(j >= coins[i-1]) dp[j] = min(dp[j], dp[j-coins[i-1]]+1);
                
            }
        }

        //因为跟第一题目不同，这里还需要判断一下
        
        int ans = dp[amount];
        if(ans == amount+1) return -1;
        else return ans;
        
    }
};

好了大功告成，如果我忘记了为什么多重背包优化成一位数组的时候是从小到大遍历，可以取重温一下y总的课，才20多分钟