2.2数学建模与MATLAB--整数规划

数学建模与MATLAB–整数规划

一、什么是整数规划？

1、整数规划定义

规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，
变量限制为整数，则称为整数线性规划。
注意：目前所流行的求解整数规划的方法，往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。

2、整数规划分类

3、整数规划的特点

二、整数规划的问题实例

生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题

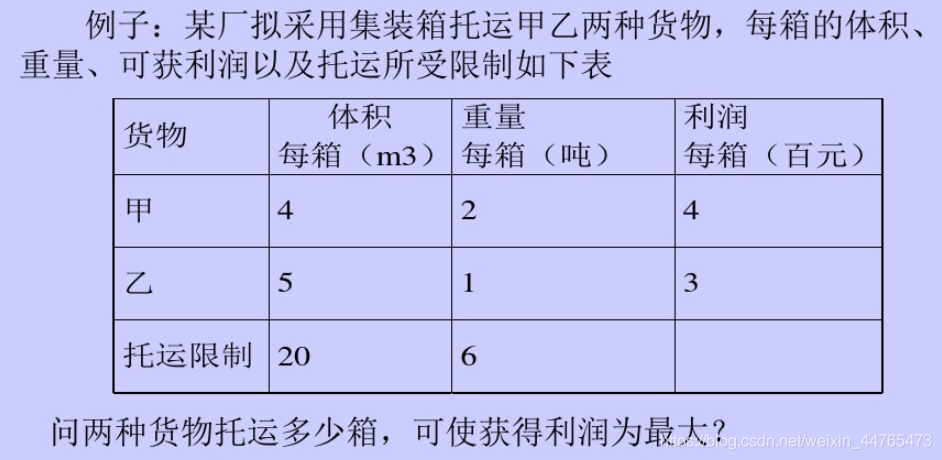
三、整数规划求解方法

1、分支定界法

求解范围：纯或混合整数线性规划
思路：
对有约束条件的最优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分枝与定界内容。通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。这就是分枝定界法的主要思路。
求解过程：

2、割平面法

求解范围：纯或混合整数线性规划<