Slot Rotation in Helib

这篇主要是描述的是BGV（Brakerski-Gentry-Vaikuntanathan）和BFV（Brakerski-Fan-Vaikuntanathan）同态加密方案中的明文空间（plaintext space）以及SIMD打包和slot 旋转计算。

BGV和BFV加密算法

Secret key generation

• 随机选取私钥 $\mathrm{sk}:=s\in R_q|$

Encryption of a plaintext polynomial

• 公开参数：明文空间$m\in R_p^r$,多项式空间$R=Z[X]/X^n+1$, 系数模q的多项式空间$R_q=Z_q[X]/X^n+1$
• 随机抽样$a\leftarrow R_q,e\leftarrow {\chi }_q|$
• BGV密文：${\text{Enc}}_s^{\mathbf{BGV}}(m;p^r)=\mathbf{c}=(\mathbf{b},\mathbf{a})=(-as+m+p^{r}e,a)\in {\mathbb{R}}_q^2$
• BFC密文：${\mathrm{Enc}}_s^{\mathbf{BFV}}(m;p^r)=\mathbf{c}==(\mathbf{b},\mathbf{a})=(-as+\lfloor \frac{q}{p^r}m\rfloor +e,a)$
  
  当在p和q互素的情况下，BGV/FV密文形式上相等
  BFV--->BGV 转换
• ${\mathbf{c}}_0=\mathrm{En}{\mathrm{c}}_{\mathrm{s}}^{\mathrm{BFV}}(\mathrm{m};{\mathrm{p}}^{\mathrm{r}})=({\mathrm{a}}_0,{\mathrm{b}}_0)=\left(-{\mathrm{a}}_0\mathrm{s}+\left[\frac{\mathrm{q}}{{\mathrm{p}}^{\mathrm{r}}}\mathrm{m}\right]+\mathrm{e},{\mathrm{a}}_0\right)\in {\mathrm{R}}_{\mathrm{q}}$
• 令
  $\begin{array}{rl}{\mathbf{c}}_1=& {-\mathrm{p}}^{\Gamma }{\mathbf{c}}_0|\\ & =\left({\mathrm{a}}_0{\mathrm{p}}^{\mathrm{r}}\mathrm{s}-{\mathrm{p}}^{\mathrm{r}}\left(e+m\frac{q}{{\mathrm{p}}^{\mathrm{r}}}\right)+{\mathrm{p}}^{\mathrm{r}}\frac{{\left[qm\right]}_{{\mathrm{p}}^{\mathrm{r}}}}{{\mathrm{p}}^{\mathrm{r}}},-{\mathrm{p}}^{\mathrm{r}}{\mathrm{a}}_0\right)=\left(-{\mathrm{a}}_1\mathrm{s}+{\mathrm{p}}^{\mathrm{r}}\mathrm{e}+{\left[qm\right]}_{{\mathrm{p}}^{\mathrm{r}}},{\mathrm{a}}_1\right)\in R_q^2\end{array}$
  BGV--->BFV 转换
• ${\mathbf{c}}_0=\mathrm{En}{\mathrm{c}}_{\mathrm{s}}^{\mathrm{BGV}}(\mathrm{m};{\mathrm{p}}^{\mathrm{r}})=({\mathrm{a}}_0,{\mathrm{b}}_0)=(-{\mathrm{a}}_0\mathrm{s}+{\mathrm{p}}^{\mathrm{r}}\mathrm{e}+\mathrm{m},{\mathrm{a}}_0)\in {\mathrm{R}}_{\mathrm{q}}$
• 令
  $\begin{array}{rl}{\mathbf{c}}_1& =[{\mathrm{p}}^{\mathrm{r}}{]}_{\mathrm{q}}^{-1}{\mathbf{c}}_0\\ & =\left(-[{\mathrm{p}}^{\mathrm{r}}{]}_{\mathrm{q}}^{-1}{\mathrm{a}}_0\mathrm{s}+\left[\frac{\mathrm{q}}{{\mathrm{p}}^{\mathrm{r}}}{q}^{-1}\mathrm{m}\right]+\mathrm{e},[{\mathrm{p}}^{\mathrm{r}}{]}_{\mathrm{q}}^{-1}{\mathrm{a}}_0\right)=\left(-{\mathrm{a}}_1\mathrm{s}+{\mathrm{p}}^{\mathrm{r}}\mathrm{e}+{\left[q^{-1}m\right]}_{{\mathrm{p}}^{\mathrm{r}}},{\mathrm{a}}_1\right)\in R_q^2\end{array}$
  

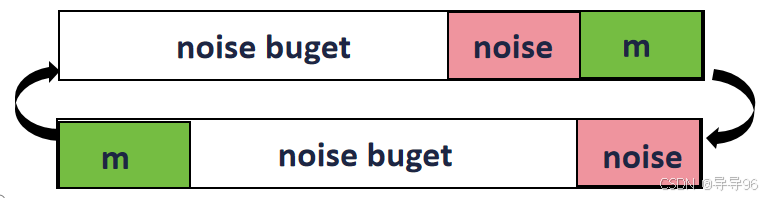
BGV同态加密SIMD编码

在全同态加密（FHE, Fully Homomorphic Encryption）中，SIMD代表 Single Instruction, Multiple Data，即单指令多数据。这是一种并行计算技术，在FHE中被广泛用于提高加密运算的效率。

系数嵌入
对于多项式$m(x)\in R_q={\mathbb{Z}}_q[x]/f(x),$其系数嵌入对应于：$m={\sum }_{i=0}^{N-1}{m}_i{X}^i$, $m(x)\mapsto (m_0,m_1,...,m_{n-1})\in {\mathbb{Z}}_q^n$，该嵌入式多项式环上元素到模q下的$n$维整数向量的映射，多项式的加法运算可对应于向量的按位加，但多项式的乘法比较复杂，不能对应向量的按位乘法。

Slot嵌入

正则嵌入定义： 令$\zeta =\exp (\pi \sqrt{-1}/n),$ 从$R_q={\mathbb{Z}}_q[x]/f(x)$到复数域 ${\mathbb{C}}^n$, 即$\sigma :a(x)\mapsto (a(\zeta ),a({\zeta }^3),...,a({\zeta }^{2n-1}))\in {\mathbb{C}}^n$，则$\sigma$为正则嵌入映射,其中$a(x)\in R_q$，$f(x)=x^n+1$。

特别地，当参数满足$q$是素数且 q = 1 ( m o d 2 n ) q=1({\mathrm{mod}}2n)