Struggle to 搞懂统计学——点估计 区间估计 置信区间

在统计学的应用过程中，总有那么几个重要的基础概念似懂非懂，就像雾里看花，你对它有一个总体的印象，但说道具体细节又似是而非。我也深受其扰，现在就结合自己的思考和网上各路大神的指点，试着通俗易懂地论述一下。

在开始之前先说一下统计学中的几个基本概念的定义，有助于后面的理解。

1. 总体（population）：是指研究对象的某个数量指标的全体。
   重点是“某个数量指标”，比如研究某个城市所有人的身高，则总体是这个城市内所有人的身高，而不是所有人。
   一般来说把总体和随机变量X等同起来。

2. 样本（sample）：
   n个相互独立且与总体X同分布的随机变量X1,X2...,Xn的整体(X1,X2,...,Xn)成来自总体 X 的容量为n的一个样本。一次抽样结果的n个值被称为样本的一个观测值或者说是样本值。

3. 统计量：
   X1,X2,...,Xn是来自总体X的样本，g(X1,X2,...,Xn)是n元函数，如果g中不包含未知参数，则称g(X1,X2,...,Xn)是样本X1,X2,...,Xn的一个统计量。
   关键点是“不含未知参数”，是“完全取决于样本的量”，说人话就是 样本均值、样本方差等就是所谓的统计量。

点估计

很简单，点估计就是用一个样本统计量来估计一个总体未知参数。
例如总体X是一个公司所有10,000名员工的年薪，目标是估计所有员工的平均年薪。点估计就是采用简单随机抽样的方法随机抽取1000名员工并统计他们的年薪，计算出1000人的平均年薪，以此来估计总体均值。当然这样是很不准的，甚至从总体X的概率密度函数上来说 P(总体均值μ-样本均值=0)=0。

区间估计

区间估计就是在点估计的基础上，给点估计值加上左右领域，给出总体参数估计的一个区间范围。
先这样简单理解一下，具体会在下面深度说明。

置信区间

理解

试想一下，我们是某大厂的员工，在职员工10,000人。
想知道自己的年薪在整个公司处于上游还是下游，但对于整个公司所有人的平均薪资我们是不知道的。
但这个总体均值μ是客观存在的，只是我们作为一名小员工不知道，我们可以认为，HR知道，假设总体的年薪服从正态分布。
HR内心OS：我知道今年所有人的平均年薪μ=100k,方差σ^2=2，也就是总体 X ~ N（100,2）,如下图

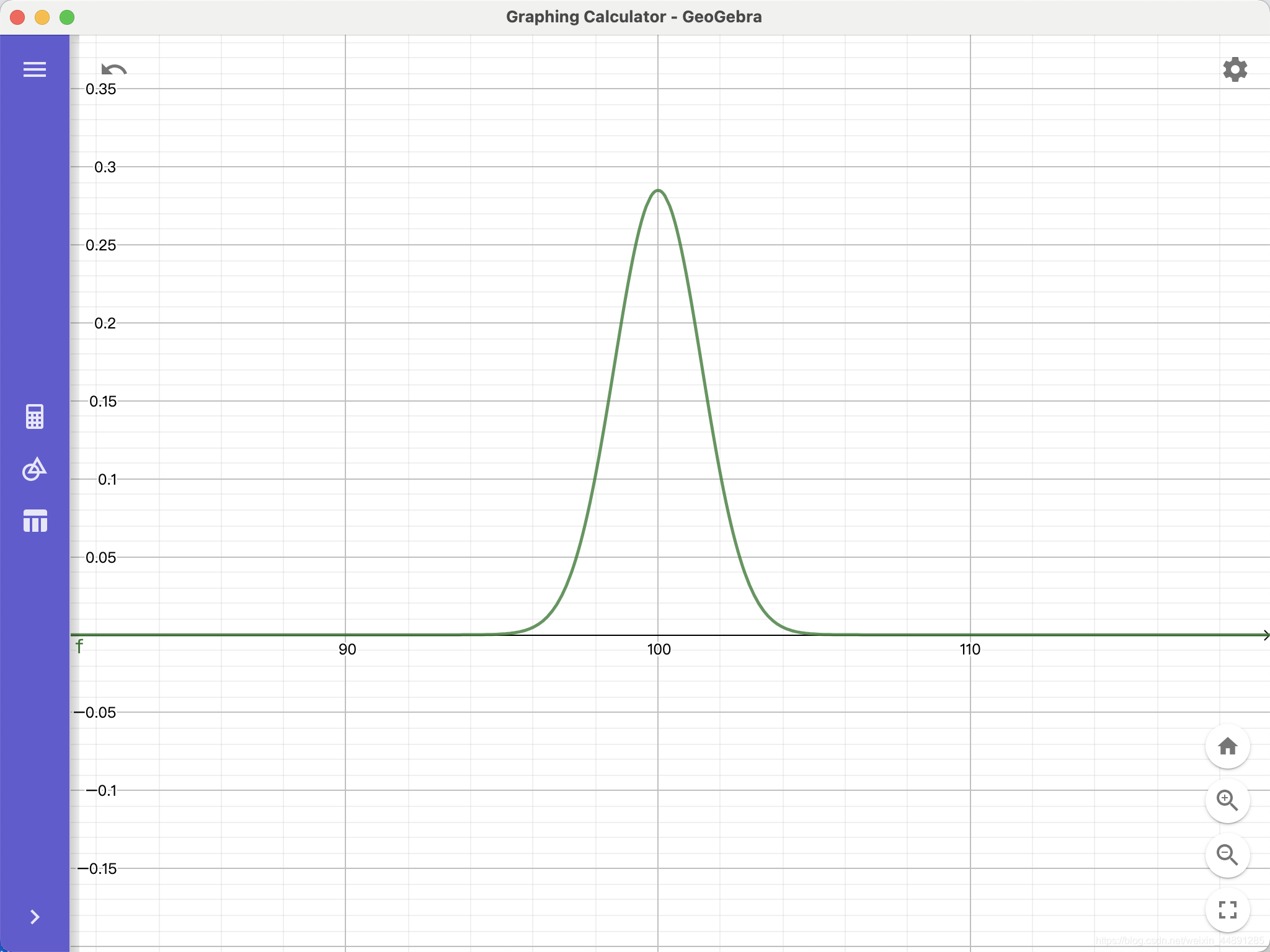
我们不可能一个一个人问过来，这样大概率也会被叫去谈话。所以随机抽取样本容量为100的同事的年薪，并计算出样本均值假设是15k，这就是点估计。

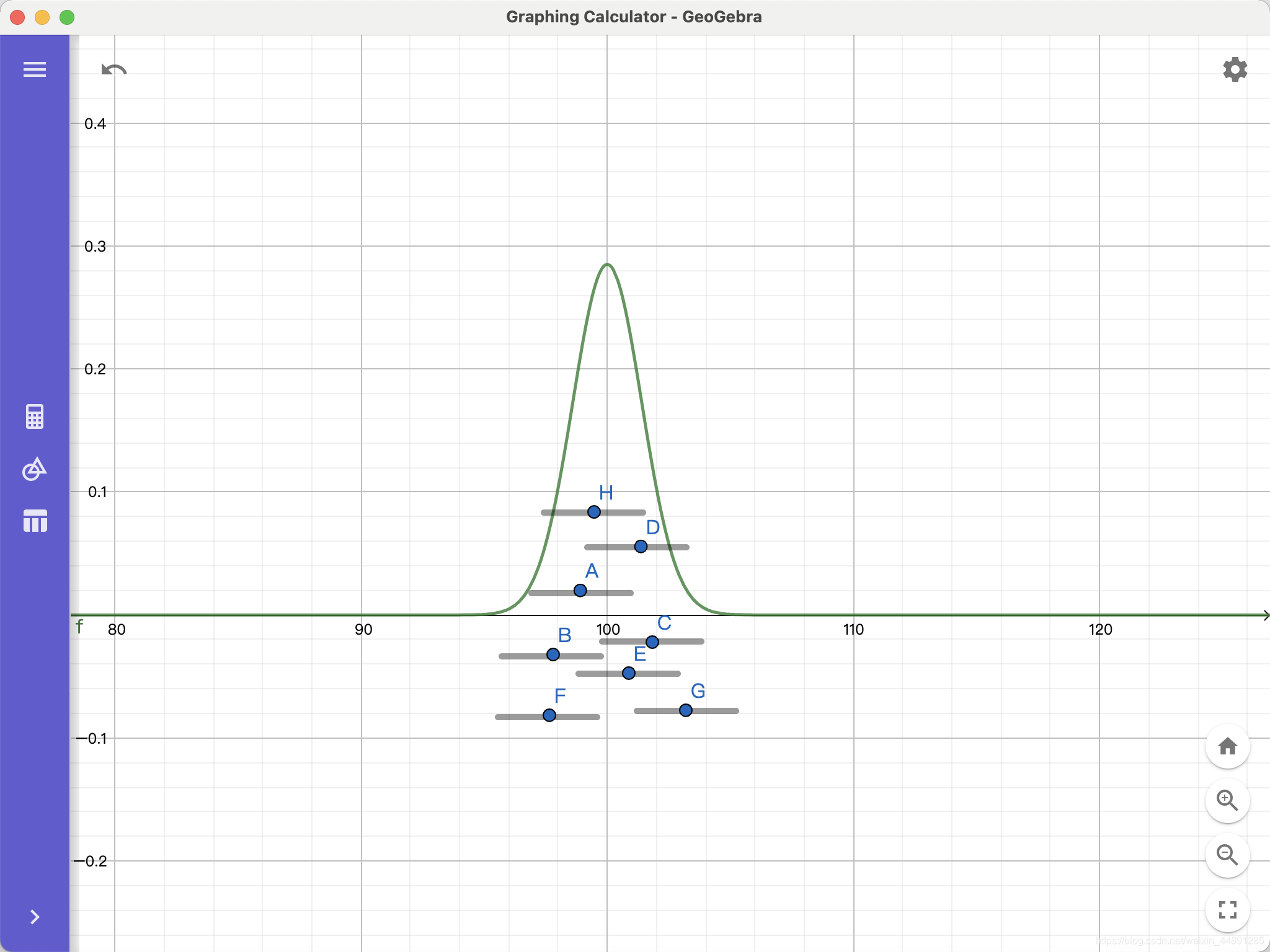
但你会想：明明我只有8k啊，为什么有15k，你觉得不准，于是经过一次又一次地抽样，得出以下的结果：

那哪个点估计更好呢？？😟😟😟咋办
于是我们采用区间估计来改善这个问题。

在95%的置信区间上,针对每个点估计构造区间估计。在HR视角下，可以发现大部分的区间估计都包含了总体均值，只有点G这一条没有包含。

但是失去了HR视角，我们还是不知道哪个区间估计更好，要是你采用了点G的区间估计，甚至不知道自己估错了。

是的，无论是点估计还是区间估计，我们都无法知道哪个点或者那个区间估计的更好，但是在95%的置信度下构造的区间估计，我们可以说，如果构造100个区间估计，那大概有95个是包含真实的总体均值的。

操作（重中之重）

以上是对区间估计的概念理解，在实际情况下，我们当然不会去构造100个区间估计。而是通过一次抽样得到的样本均值，设定显著性水平α，在 1-α 的置信区间内给出基于这个样本均值的区间估计。

接下来是数学推导
一些公式打起来不方便 就手写了

总体方差已知

设正态总体 X~N(μ,σ^2)，样本X1,X2…,Xn独立同分布于总体X，
由样本均值x的期望 E(样本均值x)=E[1/n(X1+X2+...+Xn)]=1/n * nμ=μ
方差 D(样本均值x)=D[1/n(X1+X2+...+Xn)]=1/n^2 * n * σ^2= σ ^2/n
将其标准化=> (样本均值x-μ)/(σ/√n) ~ N(0,1)

我们想要在α=0.05的显著性水平，即1-α=95%的置信区间下对总体均值μ做区间估计。
用概率表示出来是 P( |样本均值x-μ|<△)=1-α
不等号的左右恒等变形 P( |(样本均值x-μ)/(σ/√n)|<△/(σ/√n))=1-α ①

根据上面的推导，①左边服从于标准正态分布，如下图：

1-α是中间那块区域，两边的面积都等于α/2，
点K的横坐标可以用标准正态分布分位数 uα/2 表示（α=0.05）
这是一个实际已知的数，可以通过查标准正态分布分位数表获得。
所以 △= uα/2*(σ/√n)
=> P(|样本均值x-μ|<uα/2 * (σ/√n))=1-α
将式子解出来，可得
样本均值x - uα/2 * (σ/√n)<μ<样本均值x+uα/2 * (σ/√n)

总体方差未知

在现实情况中，我们往往不知道总体方差（除了HR）
那总体方差未知时应该怎么办呢😰
这时候就要用样本方差 s^2 代替总体方差 σ^2。
这里先简单介绍一下两个分布：卡方分布和t分布。

卡方分布：
随机变量X1,X2...,Xn 独立同分布于标准正态分布 N(0,1)，则
(X1 ^2 + X2 ^2 +...+Xn ^2 )服从于自由度为n的卡方分布
t分布：
随机变量 X 服从于标准正态分布，随机变量 Y 服从于自由度为n的卡方分布，且 X与Y 相互独立，则随机变量 t = X/二次根号(Y/n) 服从于自由度为 n 的 t分布。

t分布的概率密度函数图像与标准正态分布的形似，自由度n越小，则曲线越平坦，自由度n越大，曲线越接近标准正态分布，当自由度趋于+∞时，t分布就是标准正态分布。
所以在用样本方差代替总体方差做区间估计的情况下，其推导方法与用总体方差时一致，不过把标准正态分布换成了自由度为 n-1 的t分布。
所以相应的，式子
P( |总体均值μ-样本均值| < △) = 1-α
此时用t(n-1)分位数代替标准正太分位数，
△ = t(n-1)α/2分位数 * s/二次根号(n)，
总体均值的区间估计为 （μ - △ , μ + △）。

假设检验

累了，下次再讲