Noise-contrastive Estimation（NCE）学习

概述

作为现今主流自监督对比学习使用的对比损失(InfoNCE)的源头，感到学习Noise-contrastive Estimation（NCE）的重要性。该方法的原文为：Noise-contrastive estimation: A new estimation principle for unnormalized statistical models
原文很有意思，但目前很多讲解NCE的文章大都从NLP出发，这似乎无法让人清晰地看到NCE的巨大力量，事实上，NCE的理论意义应当不止于NLP。此外，还有一些写的好的讲解文章有大量公式，对于这些公式，不自己一步一步推导是无法体悟其中精髓的。因此，我打算撰写该文，尽量还原原文，逼迫自己逐行体悟其中精髓，并整理成材料，供自己加深理解。
（由于笔者水平有限，如有错漏尽请指出）

---

1. NCE文章概要学习

作者为参数化统计模型提出了一种新的估计原则。想法是执行非线性逻辑回归来区分观察到的数据和一些人为产生的噪声，使用回归非线性中的模型对数密度函数。

作者直接展示了Noise-contrastive Estimation的大概做法，即利用非线性逻辑回归区分观察到的数据和人为产生的噪声。“区分数据和噪声”这个很有意思，作者的想法从何而来？该原则又是何以工作的呢？

作者表明，这导致了参数的一致（收敛）估计，并分析了渐进方差。特别是，该方法被证明直接适用于非归一化模型，即密度函数不归一的模型。归一化常数可以像任何其他参数一样被估计。

将密度函数，即对概率分布函数求积分的值求出，用概率分布函数除以这个值（归一化常数）就自然得到了密度函数归一的模型了

对于一个可操作的ICA模型，作者将该方法与其他可用于学习非归一化模型的估计方法进行了比较，包括分数匹配（Score Matching）、对比发散（Contrastive Divergence）和最大似然（Maximum-likelihood），其中归一化常数是用重要性抽样估计的。

这里简单说明了实验条件和比较的基线。值得注意的是，Score Matching也是一个很有意义的方法。

模拟表明，噪声对比估计提供了计算和统计效率之间的最佳权衡。然后，该方法被应用于自然图像的建模。我们表明，该方法可以成功地估计一个大规模的两层模型和一个马尔科夫随机场。

这篇文章较早，放在今天，两层模型无论如何都称不上大规模了。有意思的是，马尔科夫随机场（MRF）早年在NLP中也有诸多应用。

2.NCE文章简介学习

2.1 基本估计问题描述

非标准化参数化统计模型的估计是一个计算上的难题。在此，作者提出了一个估计此类模型的新原则。
同时，该方法在无监督学习和有监督学习之间提供了一个有趣的理论联系。

这一点很有意思，这个有趣的理论联系是啥？

作者接着说，一个基本的估计问题可以表述如下：

• 假设观测到随机向量 $x\in R^n$的样本，它服从一个未知的概率密度函数（pdf）$p_d(.)$。
• 数据pdf $p_d(.)$由一个参数化的函数族 { p m ( . ; α ) } \{p_m(.;\alpha)\} {pm​(.;α)}建模。其中，$\alpha$是一个参数向量。我们假设$p_d(.)$属于这个函数族。换句话说，对于一些参数${\alpha }^{\ast }$，$p_d(.)=p_m(.;{\alpha }^{\ast })$
• 因此，考虑的估计问题就是如何通过最大化一些目标函数来从观测样本中估计$\alpha$。

显然，这个估计问题的解$\hat{\alpha }$应当使得概率密度函数满足归一化条件：
$$\int p_m(\mathbf{u};\hat{\alpha })d\mathbf{u}=1$$
这实际上定义了优化问题的一个约束。原则上，约束总是可以通过重新定义pdf来满足：
$$p_m(.;\alpha )=\frac{p_m^0(.;\alpha )}{Z(\alpha )},Z(\alpha )=\int p_m^0(\mathbf{u};\hat{\alpha })d\mathbf{u}（1）$$

这实际上是将概率分布函数的积分求出，得到归一化常数，概率分布除以这个归一化常数即满足概率密度函数积分为1的条件。

$p_m^0(.;\alpha )$为指定的pdf的函数形式，不需要满足积分和为1的条件。
然而，归一化常数（配分函数）$Z(\alpha )$的计算存在问题：积分很少是可解析处理的，并且，如果数据是高维的，数值积分是很困难的。归一化约束造成问题的统计模型的例子还可以在MRF，EBM和多层网络中找到。

这里很有意义，我们看到了马尔科夫随机场，能量模型，和多层网络与该方法的微妙联系。在之后的发展中我们可以看到基于对比的自监督学习模型事实上与能量模型也有着密切的联系。万丈高楼平地起，现在Surprise,SOTA的方法实际上都基于这些基础的概念。

如此以来，问题就变成了如何得到归一化常数$Z(\alpha )$

2.2 处理归一化常数$Z(\alpha )$的其他方案

处理归一化常数的一种概念上简单的方法是将$Z(\alpha )$作为优化模型的一个附加参数。然而，这种方法对最大似然估计（MLE）是不可能实现的。原因是，通过使$Z(\alpha )$趋于0，将使得MLE函数任意大。

为何如此呢？相关解释见附录1

因此，人们提出了直接使用$p_m^0(.;\alpha )$不计算积分，去定义归一化常数。最近的方法如对比散度（contrastive divergence）和分数匹配（score matching）。由于篇幅限制，本文将不对这两种方法进行说明。

3.NCE

3.1 NCE的定义

对于之前提到的未归一化概率密度函数pdf $p_m^0(.;\alpha )$，作者将归一化常数看成是模型的另一个常数$c$。
即：
$$ln[p_m(.;\theta )]=ln[p_m^0(.;\alpha )]+c（2）$$
其中， θ = { α , c } \theta=\{\alpha,c\} θ={α,c}。由（1）式可知，c是归一化常数$Z(\alpha )$负对数的估计。这里，$p_m(.;\theta )$只会在选择某些特定参数c的情况下归一化。
若用$X=(x_1,...,x_T)$表示观测数据集，由数据x的T个观测值组成，通过$Y=(y_1,...,y_T)$人工生成的噪声y数据集，分布为$p_n(.)$。估计量${\theta }_T$被定义为使目标函数最大化的$\theta$。该目标函数为：
$$J_T(\theta )=\frac{1}{2T}{\Sigma }_{t}ln[h(x_t;\theta )]+ln[1-h(y_t;\theta )]（3）$$

其中，
$$h(\mathbf{u};\theta )=\frac{1}{1+exp(-G(\mathbf{u};\theta ))}$$ $$G(\mathbf{u};\theta ))=ln{p}_m(\mathbf{u};\theta )-ln{p}_n(\mathbf{u})$$

这里只是定义，作者还没有解释这样设计的原因

下面，作者用$r(.)$表示逻辑函数。因此，$h(\mathbf{u};\theta )=r(G(\mathbf{u};\theta ))$

3.2 与监督学习的联系

等式(3)中的目标函数也存在于监督学习中。其是逻辑回归模型中的对数似然值，用来区分观测数据X和噪声Y。
这种与监督学习的联系，即逻辑回归和分类化，为作者提供了所提出的估计器何以工作的直觉：通过区分或比较数据和噪声，我们能够以统计模型的形式学习数据的属性。
用不太数学的语言说：噪声对比估计背后的想法是 “通过比较进行学习”。

在今天看来，“通过比较进行学习”的力量是巨大的。

为了明晰这个联系，作者展示了方程（3）中的目标函数是如何在监督学习的设置下获得的。

• 若用$U=({\mathbf{u}}_1,..,{\mathbf{u}}_{2\mathbf{T}})$表示集合X和Y的并集。并为该集合的每个数据点分配一个二进制类别标签$C_t:C_t=1$(当${\mathbf{u}}_{\mathbf{t}}\in X$)，$C_t=0$（当${\mathbf{u}}_{\mathbf{t}}\in Y$）。

在逻辑回归中，估计给定数据${\mathbf{u}}_{\mathbf{t}}$的类别的后验概率。由于数据x的概率密度函数未知，类别条件概率$p(.|C=1)$是由$p_m(,;\theta )$建模的，因此类别条件概率密度是：
$$p(\mathbf{u}|C=1;\theta )=p_m(\mathbf{u};\theta )p(\mathbf{u}|C=0)=p_n(\mathbf{u})$$
由于两个类别标签有相同的概率，即：$P(C=1)=P(C=0)=1/2$，我们得到以下后验概率：
$$P(C=1|\mathbf{u};\theta )=\frac{p_m(\mathbf{u};\theta )}{p_m(\mathbf{u};\theta )+p_n(\mathbf{u})}=h(\mathbf{u};\theta )$$$$P(C=0|\mathbf{u};\theta )=1-h(\mathbf{u};\theta )$$
类别标签$C_t$是泊努利分布的，因此参数$\theta$的对数似然函数就是：
$$l(\theta )={\Sigma }_t[C_{t}lnP(C_t=1|{\mathbf{u}}_{\mathbf{t}};\theta )+(1-C_t)lnP(C_t=0|{\mathbf{u}}_{\mathbf{t}};\theta )]$$$$={\Sigma }_{t}ln[h(x_t;\theta )]+ln[1-h(y_t;\theta )]$$
该似然函数除以1/2T，和作者提出的（3）式中的目标函数一致。

3.3 估计量的性质

作者在此分析了当样本量T足够大时候，统计量$\widehat{{\theta }_T}$的行为。弱大数定理表明，在这种情况下，目标函数$J_T(\theta )$收敛于概率J，
$$J(\theta )=\frac{1}{2}Eln[h(x;\theta )]+ln[1-h(y;\theta )]$$

就是说样本数量很大时，目标函数J收敛于J的期望

作者用$\hat{J}$表示目标J，并将其视为$f(.)=ln{p}_m(.;\theta )$的函数，即：
J ^ ( f ) = 1 2 E { l n [ r ( f ( x ) ) − l n p n ( x ) ) ] + l n [ 1 − r ( f ( y ) − l n p n ( y ) ) ] } \hat{J}(f)=\frac{1}{2}E \{ ln[r( f(x))-ln p_n(x) )] +ln[1-r(f(y) -ln p_n(y) ) ]\} J^(f)=21​E{ln[r(f(x))−lnpn​(x))]+ln[1−r(f(y)−lnpn​(y))]}
作者从描述估计量${\hat{\theta }}_T$的特征开始，描述了$\hat{J}$的优化情境。下面的定理表明（由于篇幅所限，证明被略去），数据pdf（概率密度函数） $pd(.)$ 可以通过$\hat{J}$的最大化找到，即通过在无限量数据的理想情况下学习一个分类器。

• 定理1（非参数估计） $\hat{J}$在$f(.)=ln{p}_d(.)$时取得最大值。如果选择噪声密度函数$p_n(.)$，使其在$p_d(.)$非零时非零，则不存在其他极值。

该定理的一个基本点是，在执行最大化时，对f(.)没有任何规范化约束。这与MLE形成了鲜明的对比。其中exp(f)必须积分为1。对于NCE的目标函数，不需要这样的约束。我们发现，最大化的pdf会被自动发现具有单位积分。

定理中$p_n(.)$的正向约束条件告诉我们，如果数据空间中的一些相关区域没有对比性的噪声样本，就不能推断出数据pdf pd(.)。这种情况可以通过对对比性噪声采取高斯分布等方式来轻松避免。

感觉这个有点意思

在实践中，样本数据量是有限的，$p_m(.;\theta )$的参数$\theta$数量有限。这通常有两个后果：首先，它限制了搜索数据 pdf $p_d(.)$ 的空间。 其次，它可能会将局部最大值引入优化情境。 对于这种情况下估计量的表征，通常假设 pd(.) 服从某个统计模型，例如，存在一个 ${\theta }^{\ast }$ 使得 $p_d(.)=p_m(.;{\theta }^{\ast })$。

接下来的第二个定理将告诉我们 ${\hat{\theta }}_T$ ，即（全局）最大化 $J_T$ 的 $\theta$ 的值，收敛到 ${\theta }^{\ast }$ 并因此随着样本量 T 的增加更加准确地估计$p_d(.)$ 。
对于非标准化模型，对数标准化常量是参数的一部分。这意味着作者的目标函数的最大化导致对非标准化 pdf $p_m^0(.;\alpha )$ 中的参数 $\alpha$ 和对数标准化常数 $c$ 的正确估计，这在使用似然时是不可能的。

• 定理2（一致性） 如果满足条件( a )至( c )则${\hat{\theta }}_T$有概率收敛到${\theta }^{\ast }$，即${\hat{\theta }}_T\to {\theta }^{\ast }$
  ( a ) 只要$p_d(.)$非零，$p_n(.)$就非零
  ( b ) $su{p}_{\theta }|J_T(\theta )-J(\theta )|{\to }^{P}0$
  ( c ) $I=\int \mathbf{g}(\mathbf{x})\mathbf{g}(\mathbf{x}{)}^{\mathbf{T}}P(x)p_d(x)dx$有满秩，

其中$P(x)=\frac{p_n(x)}{p_d(x)+p_n(x)}$，$g(x)={\nabla }_{\theta }ln{p}_m(x;\theta ){|}_{{\theta }^{\ast }}$

sup是单词supremum的简写，意为最小上界，即上确界。

条件 (a) 继承自定理 1，并且很容易通过选择，例如高斯噪声来实现。
条件 (b) 和 ( c) 在 MLE（最大似然估计） 中有对应的条件，参见例如（Wasserman，2004【All of statistics】. Springer）。

在 (b) 中，我们要求 $J_T$ 与 J 的概率一致性收敛； 在 MLE 中，同样需要对数似然与 Kullback-Leibler 距离的一致性收敛
条件 (c ) 确保对于大样本量，目标函数 $J_T$ 在真值 ${\theta }^{\star }$ 周围变得足够尖锐。

尖锐的意思应该就是在真值${\theta }^{\ast }$附近$J_T$足够“确定”

这通过向量 g 对模型 $p_m(.;\theta )$ 施加了一个条件。 MLE 中需要类似的约束。 对于归一化模型 $p_m(.;\alpha )$ 的估计，其中归一化常数不是参数的一部分，向量 g(x) 是 MLE 中的评分函数(score function)。 此外，如果 P(x) 是常数，则 I 将与 Fisher 信息矩阵成正比。
以下定理描述了大样本量的估计误差 $({\hat{\theta }}^T-{\theta }^{\star })$ 的分布。

• 定理 3（渐近正态性）
  $\sqrt{T}({\hat{\theta }}_T-{\theta }^{\ast })$是均值为0的渐近正态分布，其协方差矩阵为$\Sigma$
  $$\Sigma =I^{-1}-2I^{-1}[\int g(x)P(x)p_d(x)dx]\times [\int g(x{)}^{T}P(x)p_d(x)dx]I^{-1}$$
  当我们估计一个归一化模型时$p_m(.;\alpha )$，通过考虑 P(x) 是常数的假设情况，我们在这里再次观察到与 MLE 的一些相似之处：括号中的积分为零，因为它与score函数（score function）的期望成正比，而得分函数（score function）为零。 因此，协方差矩阵 Σ 的缩放常数等于 Fisher 信息矩阵。
  定理 3 得出以下推论：
• 推论 1 对于大样本量T，均方误差（MSE）$E||{\hat{\theta }}_T-{\theta }^{\ast }|{|}^2$的行为类似于$tr(\Sigma )/T$

3.4 对比噪声分布的选择

用于对比的噪声分布 pn(.) 是一个设计参数。 在实践中，我们希望噪声分布满足以下条件：

(1) 很容易从中采样，因为该方法依赖于来自噪声分布的一组样本 Y。
(2) 它允许 log-pdf 的解析表达式，以便我们可以没有问题地评估方程式（3）中的目标函数。
(3) 导致较小的均方误差 $E||{\hat{\theta }}_T-{\theta }^{\ast }|{|}^2$

我们关于一致性的结果（定理 2）也包括对 pn(.) 的一些技术限制，但它们非常温和，鉴于手头的估计问题，许多分布将验证它们。 原则上，可以最小化推论 1 中关于噪声分布 pn(.) 的均方误差 (MSE)。 然而，事实证明这非常困难，而且从这样的分布中抽样也可能并不简单。 在实践中，满足上述 (1) 和 (2) 点的众所周知的噪声分布似乎是一个不错的选择。 一些示例是高斯分布或均匀分布、高斯混合分布或 ICA 分布。

直观上，噪声分布应该接近数据分布，否则分类问题可能太简单了，不需要系统学习太多关于数据结构的知识。 以下理论结果部分证明了这种直觉：如果噪声等于数据分布，则定理 3 中的 Σ 等于 Cram´er-Rao 界限（克拉美罗下界） 的两倍。 因此，对于接近数据分布的噪声分布，我们可以保证 MSE 合理地接近理论最优值。

乍一看，这可能有悖常理。 然而，在逻辑回归的设置中，我们必须知道这两个分布是相等的，并且属于两个类中任何一个的任何点的后验概率都是 50%，这是一个定义明确的问题。

因此，可以通过首先估计数据的初步模型来选择噪声分布， 然后使用这个初步模型作为噪声分布。

这一结论具有启发意义

4 模拟

4.1 人工数据模拟

我们用 ICA 模型的估计来说明噪声对比估计 (Hyv¨arinen et al., 2001)，并将其性能与其他估计方法进行比较，即 MLE，MLE 其中归一化（配分函数）是通过重要性采样计算的（ 参见例如（Wasserman，2004）对重要性抽样的介绍），对比散度 (contrastive divergence, Hinton, 2002) 和分数匹配 (score matching, Hyv¨arinen, 2005)。 MLE 给出了性能基准。 但是，它只能在配分函数的解析表达式可用时使用。 其他方法都可以用来学习非标准化模型。

4.1.1 数据和非标准化模型

数据$x\in R^4$通过ICA模型生成
$$x=As$$
这里，$A=(a_1,...,a_4)$是$4\times 4$的混合矩阵。s 中的所有四个独立来源都遵循单位方差和零均值的拉普拉斯密度。因此，数据的的对数概率密度函数$ln{p}_d(.)$ 是
$$in{p}_d(x)=-{\Sigma }_{i=1}^4\sqrt{2}|b_i^{\ast }x|+(ln|det{B}^{\ast }|-ln4)$$
$b_i^{\ast }$是矩阵$B^{\ast }=A^{-1}$的第 i 行。非标准化模型是：
$$ln{p}_m^0(x;\alpha )=-{\Sigma }_{i=1}^4\sqrt{2}|b_{i}x|$$
参数$\alpha \in R^{16}$是行向量$b_i$。对于噪声对比估计，我们还将归一化常数视为参数并使用：
$$ln{p}_m(x;\theta )=ln{p}_m^0(x;\alpha )+c$$
标量 c 是负对数分区函数的估计值。因此，噪声对比估计的总参数集为 θ = {α, c}，而对于其他方法，参数由 α 给出。参数的真实值为 α 的矢量 $b_i^{\ast }$ 和 c的矢量$c^{\ast }=ln|det{B}^{\ast }|-ln4$ 。

4.1.2 估计方法

对于噪声对比估计，我们选择对比噪声 y 为高斯分布，具有与 x 相同的均值和协方差矩阵。 然后通过学习区分数据 x 和噪声 y，即通过最大化等式(3)中的 $J_T$ 来估计参数 θ。 优化是通过共轭梯度算法完成的 (Rasmussen, 2006)。
我们现在简要概述我们用于比较和评论我们的实施的估计方法：

在 MLE 中，选择参数 α 使得观测数据的概率最大化，即,
$$J_{MLE}(\alpha )=\frac{1}{T}{\Sigma }_{t}ln{p}_m^0(x(t);\alpha )-lnZ(\alpha )$$
被最大化。 梯度的计算由下式给出：
$${\nabla }_{\alpha }{J}_{MLE}=\frac{1}{T}{\Sigma }_t{\nabla }_{\alpha }ln{p}_m^0(x(t);\alpha )-\frac{{\nabla }_{\alpha }Z(\alpha )}{Z(\alpha )}$$
因此可以使用最速上升算法进行优化。 在我们估计 ICA 模型的实现中，我们使用了更快的自然梯度，参见例如 （Hyvarinen 等人，2001 年）。

在具有重要性采样的 MLE 中，放弃了 Z(α) 的解析表达式可用的假设。 这里，配分函数 Z(α) 是根据方程式（2）中的定义计算的，通过重要性采样，即：
$$Z(\alpha )\approx \frac{1}{T}{\Sigma }_t\frac{p_m^0(n_t;\alpha )}{p_{IS}(n_t)}$$
导数 ${\nabla }_{\alpha }Z(\alpha )$ 的计算方法相同。 样本 ${\mathbf{n}}_{\mathbf{t}}$ 是独立同分布的，并服从分布 $p_{IS}(.)$。 比例${\nabla }_{\alpha }Z(\alpha )/Z(\alpha )$ ，以及等式（20）中 $J_{MLE}$ 的梯度可用于 $J_{MLE}$ 的优化。 在作者的实现中，他们为 $p_{IS}(.)$ 和样本数 T 做出了与噪声对比估计相同的选择。

对于对比发散（contrastive divergence），请注意等式(20)中对数配分函数的梯度可以改写为：
$$\frac{{\nabla }_{\alpha }Z(\alpha )}{Z(\alpha )}=\int p_m(\mathbf{n};\alpha ){\nabla }_{\alpha }{p}_m^0(\mathbf{n};\alpha )d\mathbf{n}$$
如果我们手头有遵循模型密度 $p_m(.;\alpha )$ 的数据 $n_t$，我们可以通过取样本平均值来评估最后一个方程。 在对比发散中，通过马尔可夫链蒙特卡洛采样，创建数据 $n_t$ 大约服从 $p_m(.;\alpha )$。 在我们的实施中，我们使用了一步 Hamiltonian Monte Carlo (MacKay, 2002) 和三步蛙跳(three leapfrog steps)

对于score matching，代价函数
$$J_{sm}(\alpha )=\frac{1}{T}{\Sigma }_{t,n}\frac{1}{2}{\Psi }_n^2(x(t);\alpha )+{\Psi }_n^{\prime }(x(t);\alpha )$$
必须最小化，其中 ${\Psi }_n(x;\alpha )$ 是非标准化模型相对于 x 的第 n 个元素的导数，即 ${\Psi }_n(x;\alpha )={\partial }_{x(n)}ln{p}_m^0(x;\alpha )$ 。对于具有拉普拉斯源的ICA模型，我们得到：
$${\Psi }_n(x;\alpha )={\Sigma }_{i}g(b_{i}x)B_{in}$$$${\Psi }_n^{\prime }(x;\alpha )={\Sigma }_i{g}^{\prime }(b_{i}x)B_{in}^2$$
其中，$g(u)=\sqrt{2}sign(u)$。 我们可以在这里看到符号函数不够平滑，无法用于分数匹配。因此我们使用近似值$sign(u)\approx tanh(10u)$。这对应于假设源的逻辑密度。 然后通过共轭梯度进行优化 (Rasmussen, 2006)。

4.1.3 结果

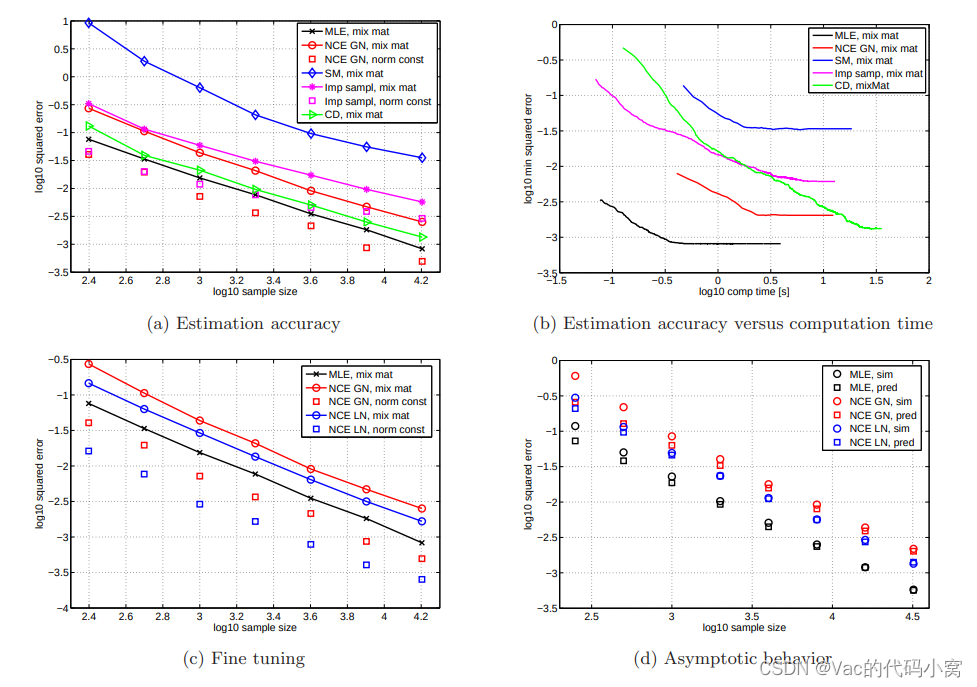
图 1：ICA 模型的噪声对比估计以及与其他估计方法的比较。 图 (a) 显示了样本量函数的估计方法的均方误差 (MSE)。 图（b）显示了计算时间函数的估计误差。 在非归一化模型的方法中，噪声对比估计 (NCE) 需要最少的计算时间才能达到所需的精度水平。图 ( c) 显示具有拉普拉斯对比噪声的 NCE 比具有高斯噪声的 NCE 产生更好的估计。 图 (d) 显示推论 1 正确描述了 MSE 对大样本量的行为。

仿真和绘图细节：图 (a)-( c) 显示了仿真结果的中值。 在 (d) 中，我们取平均值。 对于每个样本量 T ，平均基于 500 个条件数小于 10 的随机混合矩阵 A。在图 (a)、( c) 和 (d) 中，我们开始为每个混合矩阵优化 5 个不同的初始化顺序 以避免局部最优。 这对于对比散度 (CD) 来说是不可能的，因为它没有适当的目标函数。 这可能是我们在正文中指出的 CD 误差方差较高的原因。 对于 NCE 和分数匹配 (SM)，我们依靠 (Rasmussen, 2006) 的内置标准来确定收敛性。 对于其他方法，我们没有使用特定的收敛标准：它们都被赋予了足够长的运行时间以确保算法已经收敛。 在图 (b) 中，我们只对每个混合矩阵执行一次优化运行以使比较公平。 请注意，虽然其他图显示了算法收敛时的 MSE，但该图显示了运行期间的错误行为。 更详细地说，图中的曲线显示了给定时间的平均最小可能估计误差。

对于手头的任何给定方法，曲线创建如下：我们监测每个混合矩阵的估计误差和运行过程中经过的时间。 这是针对我们在图 (a) 中使用的所有样本大小完成的。 对于任何固定时间 t0，我们以这种方式获得一组估计误差，每个样本大小一个。 我们保留了最小的错误。 这给出了到时间 t0 可以实现的最小可能估计误差。 对于给定的方法，取所有 500 个混合矩阵的中值，得到图中所示的曲线。 请注意，根据构造，图中的曲线不依赖于停止标准。 将图 (b) 与图 (a) 进行比较进一步表明，对于样本量 T = 16000，(b) 中的曲线在对应于图 (a) 中的 MSE 的误差水平上变平，即 log 10(T ) ≈ 4.2 . 这是模拟中使用的最大样本量。 对于较大的样本量，曲线会在较低的误差水平下变平。

• 图1(a):

图 1 (a) 显示了不同估计方法的 MSE（$E||{\hat{\theta }}_T-{\theta }^{\ast }|{|}^2$）。 MLE 给出了参考性能（黑色十字）。 红色部分显示了噪声对比估计 (NCE) 的性能。

我们可以看到，分层矩阵 B 的误差随着样本量 T（红色圆圈）的增加而减小。 这同样适用于对数归一化常数 c（红色方块）中的误差。

这说明了估计量的一致性，因为二次均值的收敛意味着概率的收敛。 图 (a) 还显示噪声对比估计比 MLE 表现更好，其中归一化常数是通过重要性采样（Imp sampl，洋红色星号）计算的。特别是，对数归一化常数 c 的估计更准确。 对于固定的样本量，对比散度（CD，绿色三角形）在 MLE 之后产生最佳结果。
然而，应该指出的是，对比散度的平方误差分布比其他方法具有更高的方差（比噪声对比估计高约 50 倍）。 该图还显示得分匹配（SM，蓝色菱形）优于其他方法。 原因是我们不得不求助于拉普拉斯密度的近似值来进行分数匹配的估计。

• 图1 （b）:

图 1 (b) 研究了统计效率和计算效率之间的权衡。 对于给定的估计精度，MLE 需要最短的计算时间。 这反映了一个事实，即 MLE 与其他方法不同，它适用于适当归一化的密度。 在非归一化模型的方法中，噪声对比估计需要最少的计算时间才能达到所需的精度水平。 与对比发散相比，它至少快三倍。

• 图1 （c）:

图 1 (c ) 说明了使用尽可能接近数据分布的噪声分布的想法。 在第一步中，通过将数据与高斯噪声进行对比来估计混合矩阵 A 的逆 B，如图 1 (a) 所示。 在第二步中，通过将单位方差的拉普拉斯源与矩阵 $\hat{A}={\hat{B}}^{-1}$ 混合来生成对比噪声。 这种噪声的性能以蓝色显示。 我们看到使用拉普拉斯对比噪声微调参数会导致更小的 MSE 估计。 测试微调前后 MSE 差异的显着性给出 $p-value<10^{-12}$ 。

• 图1 （d）:

图 1 (d) 显示，对于大样本量 T，推论 1 正确预测了参数的 MSE：MSE 衰减为 tr(Σ)。

4.2 自然图像模拟

我们在这里使用噪声对比估计来学习自然图像的统计结构。 目前的自然图像模型可以大致分为基于块的模型和基于马尔可夫随机场（MRF）的模型。 基于补丁的模型大多是两层模型 (Osindero et al., 2006; K¨oster & Hyv¨arinen, 2007; Karklin & Lewicki, 2005)，尽管在 (Osindero & Hinton, 2008) 中三层模型是 呈现。 这些模型中的大多数都未标准化。 通常使用分数匹配和对比差异来估计它们。 为了从自然图像中学习 MRF，对比散度已在 (Roth & Black, 2009) 中使用，而 (K¨oster et al., 2009) 使用分数匹配。

4.2.1 patch模型

自然图像数据是通过从仅描绘野生动物场景的 van Hateren 数据库图像中采样大小为 30 × 30 像素的块获得的。 作为预处理，我们去除了每个patch的 DC 分量，对数据进行了白化，并将维度从 900 减少到 225。维度减少意味着我们保留了 92% 的数据方差。 作为一个新颖的预处理步骤，我们进一步标准化每个图像块，使其具有零 DC 值和单位方差。 因此，白化数据被投影到球体上。 投影到球体上可以被认为是分裂归一化（divisive normalization）的一种形式 (Lyu & Simoncelli, 2009)。 对于对比噪声，我们在球体上使用了均匀分布。

我们的patch x 模型是:
$$log{p}_m(x;\theta )={\Sigma }_n{f}_{th}(ln[v_n(Wx{)}^2+1]+b_n)+c$$
其中平方运算应用于向量 Wx 的每个元素，$f_{th}(.)$ 是平滑阈值函数。模型的参数 θ 是矩阵 $W\in R^{225\times 225}$、225 行向量 $v_n\in R^{225}$ 和定义阈值的相等数量的偏置项 $b_n$，以及用于 pdf 归一化的 c。 我们施加的唯一约束是向量 $v_n$ 被限制为非负。

我们分三步学习模型：首先，我们学习了所有参数，但保持第二层（具有行向量 $v_n$ 的矩阵 V）固定为恒等式。 第二步是在其他参数固定的情况下学习 V。 将 V 随机初始化为较小的值证明是有帮助的。 当目标函数再次达到第一步结束时的水平时，作为第三步，我们切换到同时学习所有参数。 对于优化，我们使用了共轭梯度算法 (Rasmussen, 2006)。

图2（a）显示了估计结果。 第一层特征 $w_i$（W 的行）是 Gabor-like（“简单单元”）。 第二层权重 $v_i$ 将具有相似方向和频率的特征集中在一起，这些特征不一定集中在同一位置（“复杂单元”）。 结果对应于 (K¨oster & Hyv¨arinen, 2007) 和 (Osindero et al., 2006) 中报告的结果。

4.2.2 马尔可夫随机场

我们使用与基于补丁patch的模型基本相同的数据、预处理和对比噪声。 然而，为了训练团大小为 15 像素的 MRF，我们使用了大小为 45 × 45 像素的图像块。此外，对于白化，我们采用了大小为 9 × 9 像素的白化过滤器。 没有执行冗余减少。
用 I(ξ) 表示图像 I(.) 在位置 ξ 处的像素值。 我们的图像模型 I(.) 是：
$$log{p}_m(I;\theta )={\Sigma }_{\xi ,i}{f}_{th}({\Sigma }_{{\xi }^{\prime }}{w}_i({\xi }^{\prime })I_w(\xi +{\xi }^{\prime })+b_i)+c$$
其中 $I_w(.)$ 是用白化滤波器过滤后的图像 I(.)。 模型的参数 θ 是过滤器 wi(.)（尺寸 7×7 像素），阈值 $b_i$ for i = 1 … 25，和 c 用于 pdf 的归一化。

图 2 显示了与白化滤波器卷积后学习到的滤波器 $w_i(.)$。 滤波器相当高频且类似 Gabor。 这与 (Roth & Black, 2009) 不同，后者的过滤器没有清晰的结构。 在 (K¨oster et al., 2009) 中，白色区域中显示的滤波器也类似于 Gabor。 然而，与我们的模型不同，需要对过滤器进行范数约束才能获得多个非消失过滤器。

图 2：自然图像模型的噪声对比估计。
(a) 从 255 个池化模式中随机选择 2×10 个。 每个向量 vi 对应于一个池化模式。池化模式 $i_0$ 中的补丁显示 $w_i$ ，每个补丁下的黑色条表示强度 $v_{i0}(n)$ 某个 $w_n$ 被 $v_{i0}$ 池化。
(b) 在原始空间中学习过滤器 $w_i(.)$，即在与白化过滤器卷积之后。 每个补丁下方的黑色条表示过滤器的范数。

5 结论

我们在这里提出了一种新的估计原则，噪声对比估计，它一致地估计不需要归一化的复杂统计模型（例如基于能量的模型或马尔可夫随机场）。 事实上，归一化常数可以像模型的任何其他参数一样进行估计。 估计手头的归一化常数的一个好处是它可以用来比较几个不同模型的可能性。 此外，该原理显示了无监督学习和监督学习之间的新联系。

对于易于处理的 ICA 模型，我们将噪声对比估计与可用于估计非标准化模型的其他方法进行了比较。 发现噪声对比估计比较有利。 它提供了计算和统计效率之间的最佳权衡。 然后，我们将噪声对比估计应用于基于能量的双层模型和自然图像的马尔可夫随机场模型的学习。 结果证实了估计原理的有效性：对于两层模型，我们在前两层获得了简单和复杂的细胞特性。 对于马尔可夫随机场，获得了高度结构化的类似 Gabor 的滤波器。 此外，双层模型可以很容易地扩展到更多层。 因此，我们的估计原则的一个重要潜在应用在于深度学习。

我们在之前的工作中使用了基于逻辑回归的分类来从图像中学习特征 (Gutmann & Hyv¨arinen, 2009)。 然而，在那篇论文中只学习了一层 Gabor 特征，重要的是，这种学习是启发式的，与估计理论无关。 在这里，我们展示了与统计估计的明确联系，并根据估计理论对学习进行了正式分析。 这种联系导致进一步扩展将在未来工作中处理的原则。

这一点对于我们今天依然有非常重要的意义。

---

附录1

原文提到：“处理归一化常数的一种概念上简单的方法是将$Z(\alpha )$作为优化模型的一个附加参数。然而，这种方法对最大似然估计（MLE）是不可能实现的。原因是，通过使$Z(\alpha )$趋于0，可能使可能性任意大。”这是何原因呢？

要回答这个问题，我们首先解释何为最大似然估计。

何为似然？（似然与或然）

在统计学中，似然与或然是两个重要的概念，或然（概率）指的是已知统计模型参数，利用统计模型预测接下来观测的结果。而似然则指根据观测数据结果（样本）估计统计模型的参数。因此，似然可以看成是条件概率的逆过程。

似然函数

若已知统计模型参数B，那么事件A发生概率的条件概率可以被表述为：
$$P(A|B)=\frac{P(A,B)}{P(B)}$$
根据贝叶斯定理，我们有
$$P(B|A)=\frac{P(A|B)\cdot P(B)}{P(A)}$$
这便是由观测数据A推估模型参数B的似然函数。虽然其形式上也是一种条件概率，但我们关注的变量变了。
例如，对于已知的事件A，我们推估参数B的不同可能性

最大似然估计

似然函数取得最大值表示相应的参数能够使得统计模型最为合理。 从这样一个想法出发，最大似然估计的做法是：首先选取似然函数（一般是概率密度函数或概率质量函数），整理之后求最大值点。实际应用中一般会取似然函数的对数作为求最大值的函数，即：
$$L_{MLE}={\Sigma }_{x～p_d}log(p_{\theta }(x))$$
若为原始形式似然函数，那么可以写成：
$$L_{MLE}={\Pi }_{x～p_d}{p}_{\theta }(x)$$
因此，使用对数似然函数成功地将乘积运算转换成了求和运算，在连续时，可以转为积分运算。二者的结果是一致的。

最大似然对$Z(\theta )$的估计

现在我们可以回答上面提出的问题了。若利用最大似然估计，那么利用$p_m(.;\alpha )=\frac{p_m^0(.;\alpha )}{Z(\alpha )}$构造对数似然函数，得到：
$$L_{MLE}=\int log[\frac{p_m^0(\mathbf{u};\alpha )}{Z(\alpha )}]d\mathbf{u}=E[log[\frac{p_m^0(\mathbf{u};\alpha )}{Z(\alpha )}]]$$
为了求最大值$L_{MLE}$，对参数$\alpha$求导数：
$$\frac{\partial L_{MLE}}{\partial \alpha }=E[\frac{\partial }{\partial \alpha }log[\frac{p_m^0(\mathbf{u};\alpha )}{Z(\alpha )}]]=E[\frac{\partial }{\partial \alpha }log[p_m^0(\mathbf{u};\alpha )]-\frac{\partial }{\partial \alpha }Z(\alpha )]$$
显然，通过使$Z(\alpha )$最大，将使得$L_{MLE}$最大，因此使用最大似然估计是不可能的。