ComSec第6章作业

Csome-Official

已于 2022-10-11 19:12:03 修改

阅读量520

点赞数

分类专栏： ComSec作业

于 2022-10-11 17:15:42 首次发布

本文链接：https://blog.csdn.net/weixin_45004513/article/details/127267452

版权

ComSec作业专栏收录该内容

3 篇文章 0 订阅

订阅专栏

1.描述AES中S-Box的生成过程。

初始化S-Box中的元素，第y行第x列的值为{yx}，0<=x,y<=15
将当前S-Box中的元素，在 $GF(2^8)$ 有限域中求逆，得到新的S-box
再将求过逆的S-Box元素将8位二进制进行变换，具体公式如下

$\begin{bmatrix} b_0' \\b_1' \\b_2' \\b_3' \\b_4' \\b_5' \\b_6' \\b_7' \end{bmatrix}= \begin{bmatrix} 1&0&0&0&1&1&1&1\\ 1&1&0&0&0&1&1&1\\ 1&1&1&0&0&0&1&1\\ 1&1&1&1&0&0&0&1\\ 1&1&1&1&1&0&0&0\\ 0&1&1&1&1&1&0&0\\ 0&0&1&1&1&1&1&0\\ 0&0&0&1&1&1&1&1\\ \end{bmatrix} \begin{bmatrix} b_0 \\b_1 \\b_2 \\b_3 \\b_4 \\b_5 \\b_6 \\b_7 \\ \end{bmatrix} + \begin{bmatrix} 1\\1\\0\\0\\0\\1\\1\\0 \end{bmatrix}$

2.证明公式6.9与公式6.4等价。

$\begin{align} s_{0,j}'=(2\cdot s_{0,j}) \oplus (3\cdot s_{1,j}) \oplus s_{2,j} \oplus s_{3,j} \\ s_{1,j}'= s_{0,j} \oplus (2\cdot s_{1,j}) \oplus (3\cdot s_{2,j}) \oplus s_{3,j}\\ s_{2,j}'= s_{0,j} \oplus s_{1,j} \oplus (2\cdot s_{2,j}) \oplus(3\cdot s_{3,j})\\ s_{3,j}'=(3\cdot s_{0,j}) \oplus s_{1,j} \oplus s_{2,j} \oplus (2\cdot s_{3,j}) \end{align}\tag{公式6.4}$

$\begin{align} Tmp &= s_{0,j} \oplus s_{1,j} \oplus s_{2,j} \oplus s_{3,j} \\ s_{0,j}''&= s_{0,j} \oplus Tmp \oplus [2 \cdot (s_{0,j} \oplus s_{1,j})]\\ s_{1,j}''&= s_{1,j} \oplus Tmp \oplus [2 \cdot (s_{1,j} \oplus s_{2,j})]\\ s_{2,j}''&= s_{2,j} \oplus Tmp \oplus [2 \cdot (s_{2,j} \oplus s_{3,j})]\\ s_{3,j}''&= s_{3,j} \oplus Tmp \oplus [2 \cdot (s_{3,j} \oplus s_{0,j})] \end{align}\tag{公式6.4}$

证明：
$只需证明s_{0,j}'' =s_{0,j}'，其余公式证明过程于此证明等价 \\ \begin{align} s_{0,j}'' &= s_{0,j} \oplus Tmp \oplus [2 \cdot (s_{0,j} \oplus s_{1,j})]\\ &= s_{0,j} \oplus Tmp \oplus (2 \cdot s_{0,j})\oplus(2 \cdot s_{1,j}) \\ &= s_{0,j} \oplus s_{0,j} \oplus s_{1,j} \oplus s_{2,j} \oplus s_{3,j} \oplus (2 \cdot s_{0,j})\oplus(2 \cdot s_{1,j})\\ &= (s_{0,j} \oplus s_{0,j})\oplus (2 \cdot s_{0,j}) \oplus( s_{1,j} \oplus(2 \cdot s_{1,j})) \oplus s_{2,j} \oplus s_{3,j} \\ &=(2 \cdot s_{0,j}) \oplus( s_{1,j} \oplus(2 \cdot s_{1,j})) \oplus s_{2,j} \oplus s_{3,j}\\ &= (2 \cdot s_{0,j}) \oplus(3 \cdot s_{1,j}) \oplus s_{2,j} \oplus s_{3,j}\\ &=s_{0,j}'即证 \end{align}$

3.写一个GF(2^8)的乘法函数Mul，输入GF(2^8)的两个元素a、b，输出a * b 。提示：回忆CINTA的Simple Multiplication。

GF(2^8)中m(x)={0x11b}

利用快速幂的方法，每次移位1个，检查a的最高位是否超过0x100，超过立即减去0x11b(相当于mod m(x)操作)

效率上复杂度为O(logn)，在int8中，最高的计算次数为8次循环

uint16 mulp(uint16 a, uint16 b) {
    // 传入的参数仅能传入uint8
    uint32 ans = 0;
    while (b) {
        if(b&1) ans ^= a;
        a <<= 1;
        a = a & 0x100 ? a ^ 0x11b : a;
        b >>= 1;
    }
    return ans;
}

4.写一个程序，生成AES算法中的S-Box。

根据生成的步骤，有几个难点分别是多项式求余求商、扩展欧几里得求逆、矩阵变换函数的优化

多项式求余求商

uint32 div(uint32 a, uint32 b) {
    // 传入的a、b都仅支持uint16
    uint32 remainder = a, quotient = 0;
    uint32 i, max_mul = 0x80000000;
    for(i = 1; !(b & max_mul); b<<=1, i++); // 将b移动到最高位，多项式准备除法
    for(; i; i--, b>>=1, max_mul>>=1) // 进行多项式除法，同时记录余数和商
        if(remainder & max_mul) remainder ^= b, quotient |= (1 << (i - 1));
    return remainder | (quotient << 16); // 结果高16位为商，低16位置为余数
}

扩展欧几里得求逆

uint32 exgcd(uint32 a, uint32 b) {
    // 传入的a、b均为uint16，最坏情况需要16次
    if(b == 0) return (1u << 16u);
    uint32 ab = div(a, b);
    uint32 t = exgcd(b, ab & 0xffff);
    uint16 x = t >> 16, y = t & 0xffff;
    return (t << 16) | (x ^ mul(ab>>16, y));
}

矩阵变换函数的优化

优化结果本来矩阵乘法的8*8次，优化成8次循环，那么是如何优化到这样的呢

uint8 tranfor(uint8 b) {
    // 仅用8次循环就可得到，变换结果
    uint8 ans = 0, tmp = 0b00011111;
    while (b) {
        if(b&1) ans ^= tmp;
        tmp = (tmp << 1) | uint8(bool(tmp & 0x80));
        b>>=1;
    }
    return ans ^ 0b01100011;
}

观察下列公式，发现矩阵乘法行乘列之后只能得到1位的值，考虑能否同时得到8位的值
$\begin{bmatrix} b_0' \\b_1' \\b_2' \\b_3' \\b_4' \\b_5' \\b_6' \\b_7' \end{bmatrix} = \begin{bmatrix} 1&0&0&0&1&1&1&1\\ 1&1&0&0&0&1&1&1\\ 1&1&1&0&0&0&1&1\\ 1&1&1&1&0&0&0&1\\ 1&1&1&1&1&0&0&0\\ 0&1&1&1&1&1&0&0\\ 0&0&1&1&1&1&1&0\\ 0&0&0&1&1&1&1&1\\ \end{bmatrix} \begin{bmatrix} b_0 \\b_1 \\b_2 \\b_3 \\b_4 \\b_5 \\b_6 \\b_7 \\ \end{bmatrix}+ \begin{bmatrix} 1\\1\\0\\0\\0\\1\\1\\0 \end{bmatrix}$
故做如此变换
$\begin{align} \begin{matrix} (1&0&0&0&1&1&1&1)&\oplus&c_0&->&b_0'\\ (1&1&0&0&0&1&1&1)&\oplus&c_0&->&b_1'\\ (1&1&1&0&0&0&1&1)&\oplus&c_0&->&b_2'\\ (1&1&1&1&0&0&0&1)&\oplus&c_0&->&b_3'\\ (1&1&1&1&1&0&0&0)&\oplus&c_0&->&b_4'\\ (0&1&1&1&1&1&0&0)&\oplus&c_0&->&b_5'\\ (0&0&1&1&1&1&1&0)&\oplus&c_0&->&b_6'\\ (0&0&0&1&1&1&1&1)&\oplus&c_0&->&b_7'\\ \&&\&&\&&\&&\&&\&&\&&\&&\\ b_0 &b_1 &b_2 &b_3 &b_4 &b_5 &b_6 &b_7 \end{matrix}\\ \end{align}$
情况豁然开朗，只需要按列来保存，遍历 $b_0,b_1,b_2,b_3,b_4,b_5,b_6,b_7)$ ，中的每一位，如果当前位是1，则ans异或上对应变换矩阵的列，最后只需要异或一下 $c$ 即可，复杂度从8*8降到了8

再次观察列的分布规律，发现随着 $b_i$ ，中i的增大，列也呈现循环移位的情况。即

tmp = 0b00011111;
tmp = (tmp << 1) | uint8(bool(tmp & 0x80));

故最后的代码

uint8 tranfor(uint8 b) {
    // 仅用8次循环就可得到，变换结果
    uint8 ans = 0, tmp = 0b00011111;
    while (b) {
        if(b&1) ans ^= tmp; // 检查当前位是否为1，是则异或当前矩阵的列
        tmp = (tmp << 1) | uint8(bool(tmp & 0x80 //循环移位
        b>>=1;
    }
    return ans ^ 0b01100011; // ans ^ c
}

最终生成S-Box代码

#include<stdio.h>

typedef unsigned int uint32;
typedef unsigned short uint16;
typedef unsigned char uint8;

uint32 div(uint32 a, uint32 b) {
    // 传入的a、b都仅支持uint16
    uint32 remainder = a, quotient = 0;
    uint32 i, max_mul = 0x80000000;
    for(i = 1; !(b & max_mul); b<<=1, i++);
    for(; i; i--, b>>=1, max_mul>>=1)
        if(remainder & max_mul) remainder ^= b, quotient |= (1 << (i - 1));
    return remainder | (quotient << 16);
}

uint32 mul(uint32 a, uint32 b) {
    uint32 tmp, ans = 0;
    while (tmp=a&(-a)) {
        ans ^= tmp * b; // 机器优化乘法，此处tmp一定为2的幂
        a -= tmp;
    }
    return ans;
}

uint32 mulp(uint32 a, uint32 b, uint32 p) {
    uint32 ans = 0, tp = p, flag;
    while (tp-=tp&(-tp)) flag = tp;
    while (b) {
        if(b&1) ans ^= a;
        a = a << 1;
        a = a & flag ? a ^ p : a;
        b >>= 1;
    }
    return ans;
}

uint8 tranfor(uint8 b) {
    // 仅用8次循环就可得到，变换结果
    uint8 ans = 0, tmp = 0b00011111;
    while (b) {
        if(b&1) ans ^= tmp;
        tmp = (tmp << 1) | uint8(bool(tmp & 0x80));
        b>>=1;
    }
    return ans ^ 0b01100011;
}

uint32 exgcd(uint32 a, uint32 b) {
    // 最坏情况需要16次
    if(b == 0) return (1u << 16u);
    uint32 ab = div(a, b);
    uint32 t = exgcd(b, ab & 0xffff);
    uint16 x = t >> 16, y = t & 0xffff;
    return (t << 16) | (x ^ mul(ab>>16, y));
}

uint8 S_box[256];

int main() {
    // 综合复杂度16次即可求逆+变换
    for(uint32 i = 1; i <= 255; ++i) S_box[i] = tranfor(uint8(exgcd(i, 0x11b) >> 16));
    S_box[0] = tranfor(0);
    for(uint32 i = 0; i < 16; ++i) {
        for(uint32 j = 0; j < 16; ++j) {
            printf("%02x ", S_box[i * 16 + j]);
        }
        printf("\n");
    }
}

output

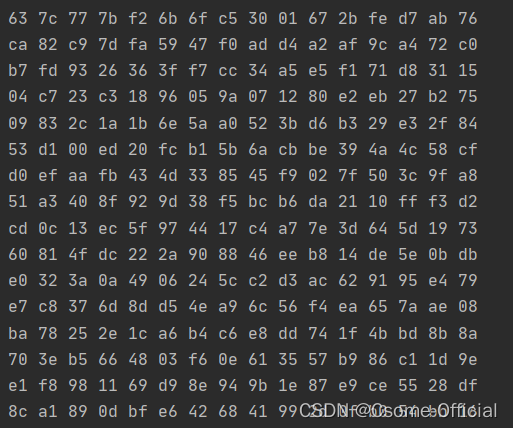
63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76
ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0
b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15
04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75
09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84
53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf
d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8
51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2
cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73
60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db
e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79
e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08
ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a
70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e
e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df
8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16