数独-比回溯法更优的人类思维逻辑的数独解法

数独规则

数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次。此处出现的候选数我们稍后再提。

※不要求斜线也满足条件

最常规的回溯法

对于常规，也可以说是最常使用的一种算法，回溯法。它可以用来解决很多问题，比如这里的数独问题。
先说说它的优点，对于程序员来说，代码量很少，往往几层嵌套循环就可以解决问题，逻辑也很简单， 编写也很快捷。但这里我们为什么不推荐使用呢，因为它对于这个问题，时间复杂度有些高。
首先这个算法类似与我们平时说的试。先对于一个空格，依次读取该格所在行，所在列，所在宫，保证所填数与三者中任一数都不重复。比如上面的图，第一行第二列那个格，检查该行列宫后，出现数为123567，所以它可以填489，根据回溯法，就填4，然后看第二空格，以此类推，直到有一空格没有数字可填，则将上一空格所填数更改，如果该格也没有可以更改的数，那么再退上一格。。。。。所以到后来，如果运气不好，这个方法可能会试非常非常多次，所以我认为对于单纯的计算机效率来说，这个方法不算优。

再看这

此时，再将我要写的算法之前，先讲一下人工数独解法。此处要引入一个概念，叫做候选数。
候选数顾名思义，就是候选的数字。对于每一个要填的空格，都有一个候选数组。比如第一行第二列的那个空格，489就是它的候选数，如果还是不懂，百度一下你就知道！

第一种，唯一候选数法

其实这些解法只是数独解法的冰山一角，往往一个复杂的数独题目要使用很多很多的方法。具体可参考这里 但是对于实现起来的逻辑，我挑选了一共两种解法交替使用。第一种，也是最好用的，唯一候选数法。即按照上面提到的，将每一个空白格按照行列宫依次查找，最后得出其候选数组，然后找到那个候选数组中候选数个数为1的，说明这个格只能填这个数字，然后填入。之后更新所填格所在的行列宫的其他空白格的候选数组，也就是减去新填入的这个数字。

当某行已填数字的宫格达到8个，那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。成为行唯一解。
唯一候选数法的思路是：选定一个空白格，从其初始候选数中删除与它在同一行、同一列以及同一宫中已经确定的数字，当这一格的候选数为1时，这一格正确的数字就是剩下的唯一一个候选数。如此重复，直至找到全部解或者无法再用此方法进行下去。
比如这个题，我们可以发现中间那个格子，填5，然后将该行列宫中所有的候选数都删去5，发现该行第二列那个各自只能填2，依次类推，到后来会出现越来越多的唯一候选数格子。

第二种，隐式唯一候选数法

与第一种方法类似，只是有时我们发现所有空白格中，没有一个候选数个数为1的，此时第一种方法已经行不通了，我们就要用到隐式法了。虽然表面上没有候选数
当某个数字在某一行（列、宫）各单元格的候选数中只出现一次时，那么这个数字就是这一列的唯一候选数了．这个单元格的值就可以确定为该数字． 这时因为，按照数独游戏的规则要求每一行（列、宫）都应该包含数字1～9，而其它单元格的候选数都不含有该数，则该数不可能出现在其它的宫格，那么就只能出现在这个宫格了。

比如这个题，会发现没有唯一候选数格子，此时第一种方法失败，然后用第二种方法，可以发现第三行第七列中候选为5的那个格子，该行的候选数中再没有出现5，所以这里必填5，然后更新该行列宫的候选数，以此方法，一旦出现候选数为1的格子，立刻停止此方法，调用第一个方法，直到第一个方法再次失败，再调用此方法。

plan B

如果两种方法都失败了呢？那就无可奈何了，我的算法逻辑仅写到这里。有兴趣的朋友可以写更多的算法，根据上面提到的链接，或者百度一下数独的解法。
但对于我的方法就结束了，这时数独如果还没解完怎么办？那就回到经典的回溯法去解了。但有人也许会问，这不还是一样吗？还是需要回溯法。
其实不然，回溯法之所以对于复杂数度题目解起来很慢，是因为空白格太多，所以可能的情况太多了。而此时我们经过上面两种方法交替使用后，可以发现填出来很多格子，再不济只填出一个格子，那样对于回溯法来说，少的复杂度也是几何倍数的。所以总体来说，经过上面两种解法解过的数度题，要不解完，要不难度也不会很大了。此时调用回溯法完善就很快捷了。
PS：如果上面两种方法一个空白格也填不出来，我也没办法了，因为数独解法太多了，有兴趣的朋友可以继续写写Plan c，Plan d。。。。

此处附上我的测试

就下图这个较为复杂数独来说，比如此时右侧数独，因为所给数不多，而且分布较为集中，所以此时若按常规的回溯方法来解，势必回有较大的复杂度。

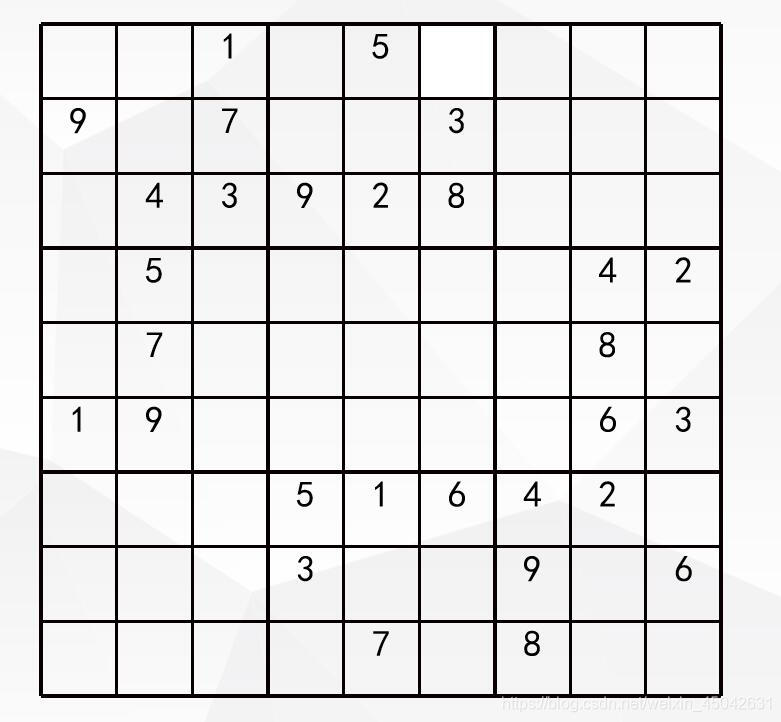
我在同一台设备上进行了多次重复实验。单一采用回溯法，我们解题大概需要0.28s左右

但用了我的两种方法后，数独变成了这个样子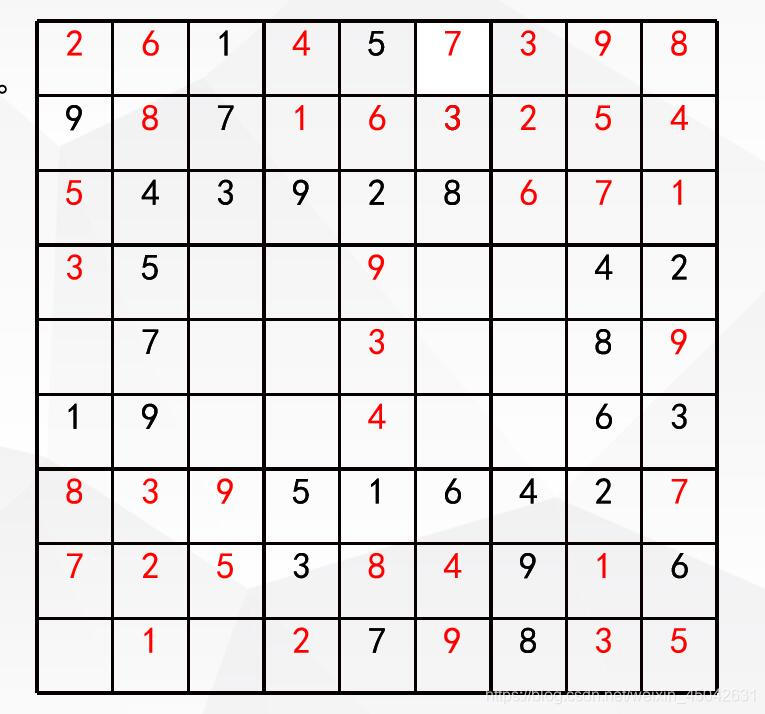
此时我的两种方法都用不了了，调用Plan B回溯法，但就这么几个空白格，相信人都可以手动推算出来，所以此时时间复杂度大大降低。

而当我们使用综合方法时，此时的时间大致在0.16s左右

※也许看起来快了其实并没有多少，但是你要知道，这么复杂的题目，对于计算能力恐怖的计算机来说，对于计算机来说，0.01s的优势都是多大的优化。

但是对于一些简单的数独题目，这个方法的优势就不是很大了
下图是回溯法的

这是我的方法的

但对于复杂题目，再来个例子
回溯法的

我的

还是快了很多哦！

写在最后

第一次写这个博客，可能说的不是很清楚，我也只是一个大二学生，程序小白，这个代码的优化程度根本不够，而且逻辑很复杂，很庞大。总之，写的太傻了，但是我认为的比较好的解数独方法，大家不要杠我~~最后欢迎各位提个意见！

附上代码

觉得不错的话，记得顶一下哦！
有问题可以评论区留言哦

#include<stdio.h>
#include<string.h>
#include<stdlib.h>

//原题
/*int a[9][9]={
   {5,3,0,0,7,0,0,0,0},
             {6,0,0,1,9,5,0,0,0},
             {0,9,8,0,0,0,0,6,0},
             {8,0,0,0,6,0,0,0,3},
             {4,0,0,8,0,3,0,0,1},
             {7,0,0,0,2,0,0,0,6},
             {0,6,0,0,0,0,2,8,0},
             {0,0,0,4,1,9,0,0,5},
             {0,0,0,0,8,0,0,7,9}};*/
//难度3
/*int a[9][9]={
   {0,0,0,1,0,0,2,6,0},
             {7,0,0,0,3,0,0,0,0},
             {3,0,2,0,8,0,4,0,0},
             {0,0,0,4,0,8,0,0,1},
             {0,3,5,0,0,0,9,4,0},
             {2,0,0,3,0,5,0,0,0},
             {0,0,6,0,5,0,7,0,9},
             {0,0,0,0,4,0,0,0,8},
             {0,5,7,0,0,9,0,0,0}};*/
//难度4

/*int a[9][9]={
   {0,0,1,0,5,0,0,0,0},
               {9,0,7,0,0,3,0,0,0},
               {0,4,3,9,2,8,0,0,0},
               {0,5,0,0,0,0,0,4,2},
               {0,7,0,0,0,0,0,8,0},
               {1,9,0,0,0,0,0,6,3},
               {0,0,0,5,1,6,4,2,0},
               {0,0,0,3,0,0,9,0,6},
               {0,0,0,0,7,0,8,0,0}};*/
/*int a[9][9]={
   {0,1,0,0,0,8,4,0,7},
             {9,5,0,0,0,0,0,0,0},
             {0,0,8,0,1,0,0,0,0},
             {0,8,2,0,0,0,0,0,0},
             {7,0,0,4,0,6,0,0,8},
             {0,0,0,0,0,0,6,2,0},
             {0,0,0,0,5,0,7,0,0},
             {0,0,0,0,0,0,0,8,2},
             {5,0,3,2,0,0,0,1,0}};*/

//难度5
int a[9][9]={
   {
   9,0,0,0,1,7,0,0,2},
             {
   5,6,3,0,0,0,0,0,0},
             {
   0,0,0,0,0,0,0,0,0},
             {
   0,0,0,5,0,0,0,8,0},
             {
   0,7,0,0,0,0,4,0,0},
             {
   0,2,0,0,0,0,0,3,0},
             {
   8,0,0,3,0,0,0,0,0},
             {
   4,0,0,0,0,0,0,0,7},
             {
   0,0,0,0,0,0,0,0,0}};

/*int a[9][9]={
   {9,0,0,0,1,7,0,0,2},
             {5,6,3,0,0,0,0,0,0},
             {0,0,0,0,0,0,0,0,0},
             {0,0,0,5,0,0,0,8,0},
             {0,7,0,0,0,0,4,0,0},
             {0,2,0,0,0,0,0,3,0},
             {8,0,0,3,0,0,0,0,0},
             {4,0,0,4,8,9,0,0,7},
             {0,0,0,0,0,0,0,0,0}};*/

struct King
{
   
	int num;
	int candidata[9] = {
   1,2,3,4,5,6,7,8,9};  //候选字数组
	int row;
	int line;
	int Gnum;
	int cannum = 9;
};

struct King shudu[81];
int G[9];
int check = 0;      //检查标志，若数独完成，则check = 1
int measure1 = 0,measure2 = 0,measure3 = 0;     //判断使用哪些方法


void del(King *shudu,int num);
int read(int candidata[]);
int update(int row,int line,int Gnum,int num);
void seek();
void sub(int backup[],int candidata[]);
void implicit();
void search(int n);
int canplace(int n,int i);
void output();
void renew();
void out();

int main()
{
   
	int i,j;
    int m,n,b;
    int e,d;
    int answer = 1;     //数独解情况
    printf("解数独程序开始！\n原数独为：\n");
    output();
    printf("\n数独解为：\n");
	for(i=0;i<9;i++<