【40. 石子合并（区间DP）】

1. 思路

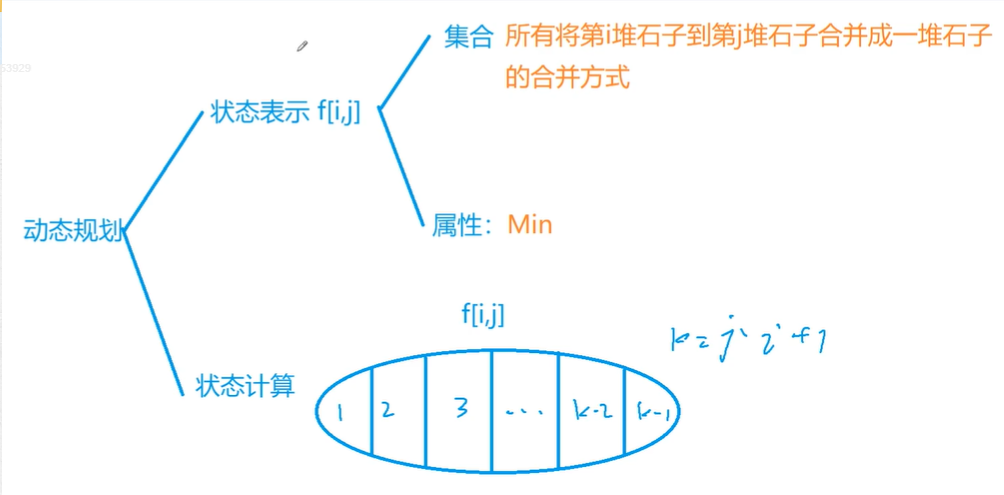
• 在定义状态的时候，与线性DP和背包问题不一样，这里是定义了一个区间

• 状态表示

  • f[i][j]表示一个区间,第i 堆石子到第j堆石子这个区间
  • 集合：所有将第i堆石子到第j堆石子合并成一堆石子的合并方式
  • 属性：这些合并方式中，代价最小值

• 关键点：

  • 最后一步一定是将俩堆合并成一堆（因此可以将最后一次合并的分界线位置进行分类）
  • 先将分界线左边进行合并，再将分界线右边合并，最后再将这俩堆进行合并(此时就需要前缀和)

• 状态计算

  • 总共的最小代价，是每类的最小代价，在取最小值，每一类最小代价求法(左边的最小代价 + 右边的最小代价 + 最后俩堆合并成一堆的最小代价)
    

• 枚举顺序：

  • 很明显，长的区间由短的区间合并而成
  • 所以先枚举区间长度 lenlen
    接着枚举左端点 l（ 右端点由左端点和区间长度去确定）
  • 最后枚举分段点 k，计算 dp 方程

• 最后结果

  • f[1][n]

1.1 时间复杂度

• 状态的数量是俩维所以是n²,状态的计算是要枚举一个k，k是O(n),总的时间复杂度是O(n³)，题目n = 300,300³ = 2.7*10⁷,一秒中可以计算出来

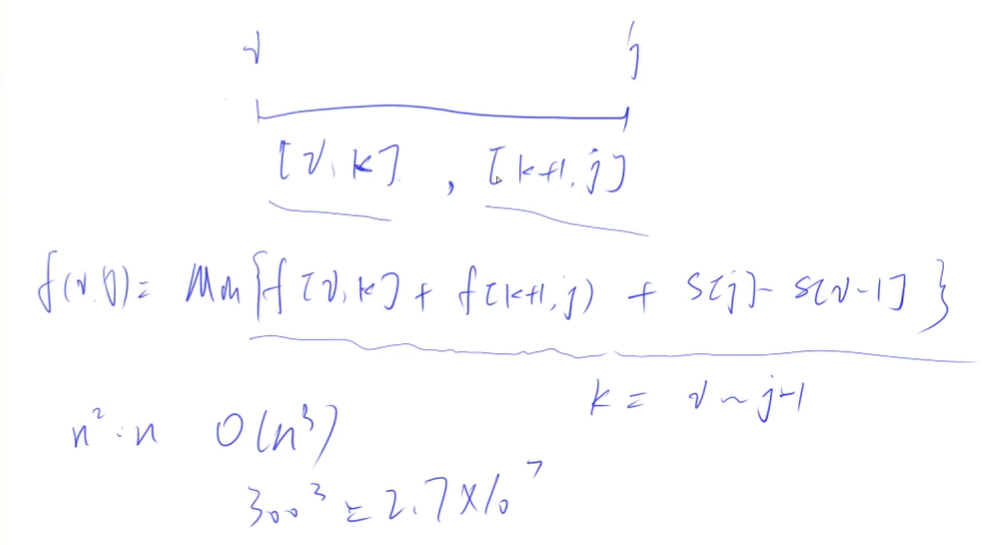
1.2 前缀和可以和之前的做对比

'序列:2 1 3 6 4'

a[i]; //代表值
s[i]; //代表前缀和

'方法1：直接输入s[i]'
 for (int i = 1; i <= n; i ++) cin >> s[i];
 for (int i = 1; i <= n; i ++) 
    {
        s[i] += s[i - 1] ; 
        cout << s[i] << endl;
    }
    
'方法2：直接输入a[i]'
 for (int i = 1; i <= n; i ++) cin >> a[i];
 for (int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i];

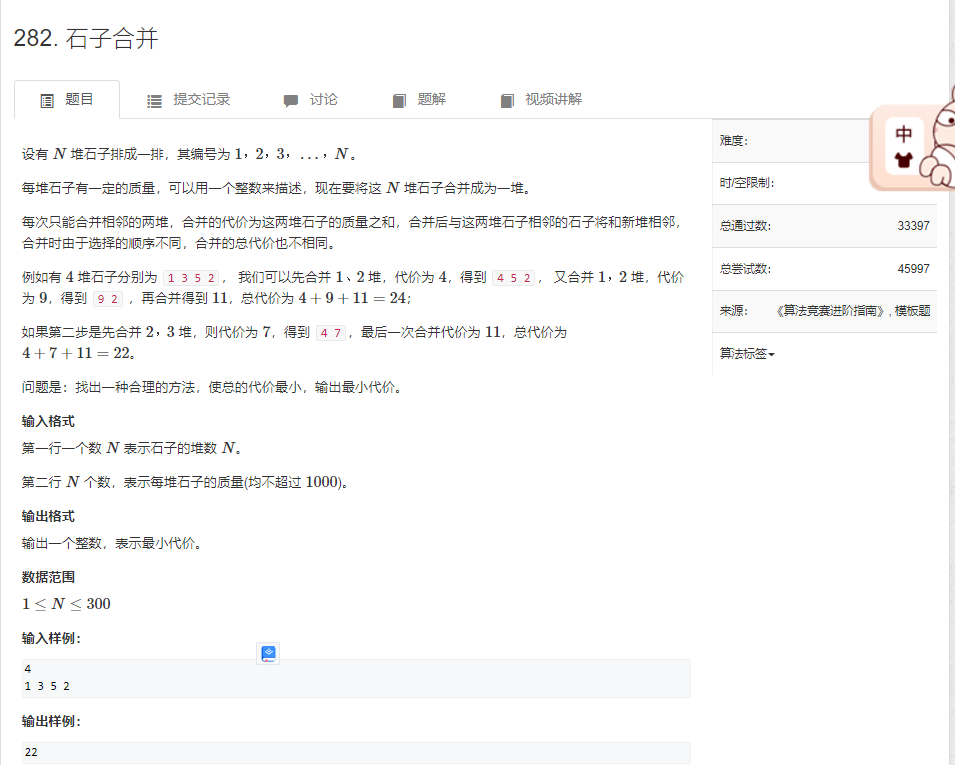
2. 题目

3. 代码

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 310;
int n;
int s[N];     //前缀和，进行最后一堆合并时，它的代价是所有堆的和
int f[N][N];


int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> s[i];
    
    for (int i = 1; i <= n; i ++) s[i] += s[i - 1]; //处理前缀和
    
    //边界情况下是区间长度为1的时候，此时只有一堆，合并不需要代价0，因为f[N][N]是全局数组，所以本来就是0，
    //所以直接从长度为2开始计算。
    for(int len = 2; len <= n; len ++)              //长度从小到大枚举所有状态
    {
        for (int i = 1; i + len - 1 <= n; i ++)     //枚举起点（左右端点就可以计算）
        {
            int l = i, r = i + len - 1;
            f[l][r] = 1e8;                      //进行初始化
            for (int k = l; k < r; k ++)        //枚举分界点k
            {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    }
    cout << f[1][n];
    return 0;
}

#include<bits/stdc++.h>
using namespace std;

const int N=310,INF=0x3f3f3f3f;
int f[N][N];
int s[N];
int n;

int main(){
    cin>>n;
    memset(f,INF,sizeof(f));     //记得初始化
    for(int i=1;i<=n;i++){
         cin>>s[i];
         f[i][i]=0;             //初始化，本身自己不需要合并，所以需要的体力为0
    }
    for(int i=1;i<=n;i++) s[i]+=s[i-1];

    for(int len=2;len<=n;len++){
        for(int l=1;l+len-1<=n;l++){
            int r=l+len-1;
            for(int k=l;k<r;k++){
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }    
        }
    }
    cout<<f[1][n]<<endl;
    return 0;
}

• 类似于归并排序，先进行集合的划分，然后很对划分好的集合再次进行划分，最后合成一堆
  

注意1（所有区间DP的通病）

• 不好循环，要保证计算每个f[i][j]的时候，f[i][j]用到的所有状态都必须是已经计算好的，所以需要一个顺序，保证在计算的时候保证计算当前状态时，所用到的其他状态都计算好了
• 区间DP的顺序可以枚举区间程度(按照区间长度从小到大来做)

注意2

• 可以用递归来代替for循环
• 动态规划尤其是区间DP可以写成递归的写法（也叫做记忆化搜索），容易理解，记忆搜索后面将，目前尽可能写成循环形式
• 区间DP一般从小到大循环（先循环区间长度），在循环区间的左端点，最后枚举决策

4. 区间DP常用模板

for (int len = 1; len <= n; len++) {         // 区间长度
    for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
        int j = i + len - 1;                 // 区间终点
        if (len == 1) {
            dp[i][j] = 初始值
            continue;
        }

        for (int k = i; k < j; k++) {        // 枚举分割点，构造状态转移方程
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
        }
    }
}