【44. 状态压缩DP（蒙德里安的梦想）】

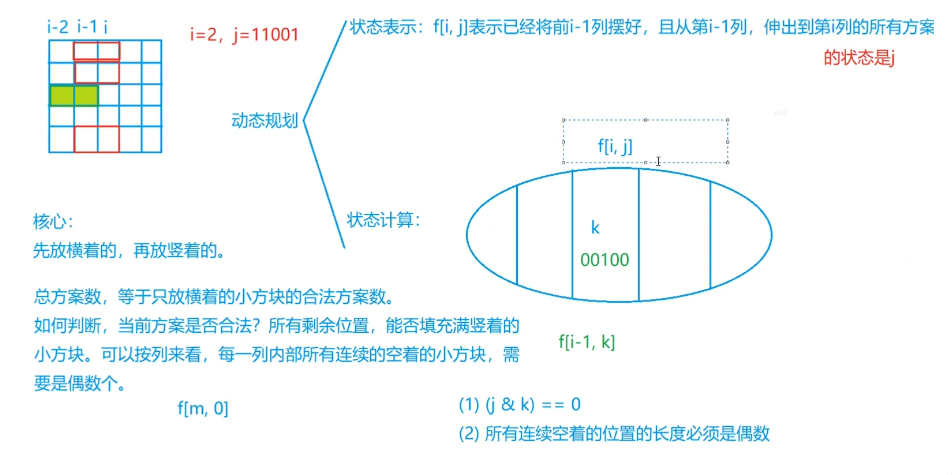
核心：

• 摆放方块的时候，先放横着的，再放竖着的。总方案数等于只放横着的小方块的合法方案数。

如何判断，当前方案数是否合法？

• 所有剩余位置能否填充满竖着的小方块。可以按列来看，每一列内部所有连续的空着的小方块需要是偶数个。

• 这是一道动态规划的题目，并且是一道 状态压缩的dp：用一个N位的二进制数，每一位表示一个物品，0/1表示不同的状态。因此可以用0→2N−1（N二进制对应的十进制数）0→2N−1（N二进制对应的十进制数）中的所有数来枚举全部的状态。

状态表示

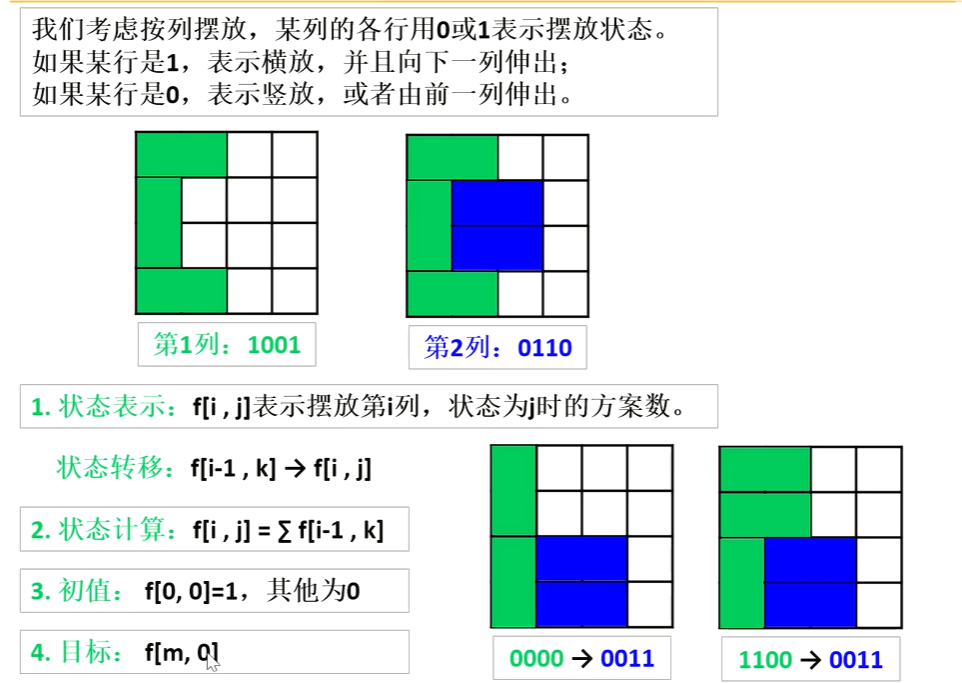
• f[i][j] 表示已经将前 i -1 列摆好，且从第i−1列，伸出到第 i 列的状态是 j 的所有方案。其中j是一个二进制数，用来表示哪一行的小方块是横着放的，其位数和棋盘的行数一致。

状态转移

• 既然第 i 列固定了，我们需要看 第i-2 列是怎么转移到到第 i-1列的（看最后转移过来的状态）。假设此时对应的状态是k（第i-2列到第i-1列伸出来的二进制数，比如00100），k也是一个二进制数，1表示哪几行小方块是横着伸出来的，0表示哪几行不是横着伸出来的。

• 它对应的方案数是f[i−1,k]f[i−1,k]，即前i-2列都已摆完，且从第i-2列伸到第i-1列的状态为 k 的所有方案数。

这个k需要满足什么条件呢?

• 首先k不能和 j在同一行（如下图）：因为从i-1列到第i列是横着摆放的12的方块，那么i-2列到i-1列就不能是横着摆放的，否则就是1 3的方块了！这与题意矛盾。所以 k和j不能位于同一行。

• 既然不能同一行伸出来，那么对应的代码为(k & j ) ==0 ，表示两个数相与，如果有1位相同结果就不是0， (k & j ) ==0表示 k和j没有1位相同， 即没有1行有冲突。

• 既然从第i-1列到第i列横着摆的，和第i-2列到第i-1列横着摆的都确定了，那么第i-1列 空着的格子就确定了，这些空着的格子将来用作竖着放。如果 某一列有这些空着的位置，那么该列所有连续的空着的位置长度必须是偶数。

总共m列，我们假设列下标从0开始，即第0列，第1列……，第m-1列。根据状态表示f[i ] [j] 的定义，我们答案是什么呢

• f[m][0]， 意思是 前m-1列全部摆好,且从第m-1列到m列状态是0（意即从第m-1列到第m列没有伸出来的）的所有方案，即整个棋盘全部摆好的方案。

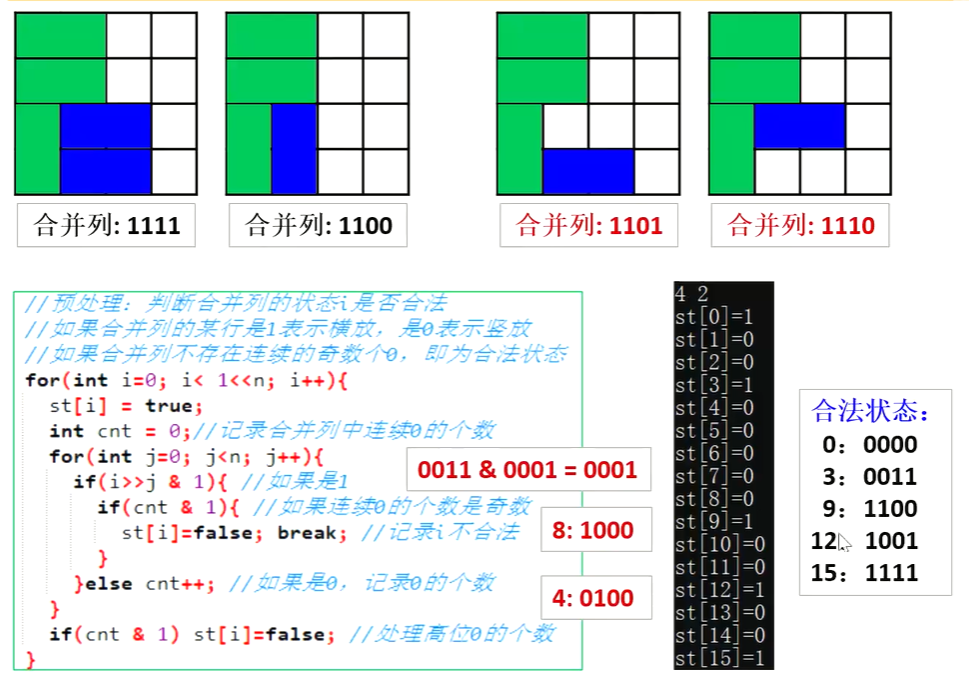
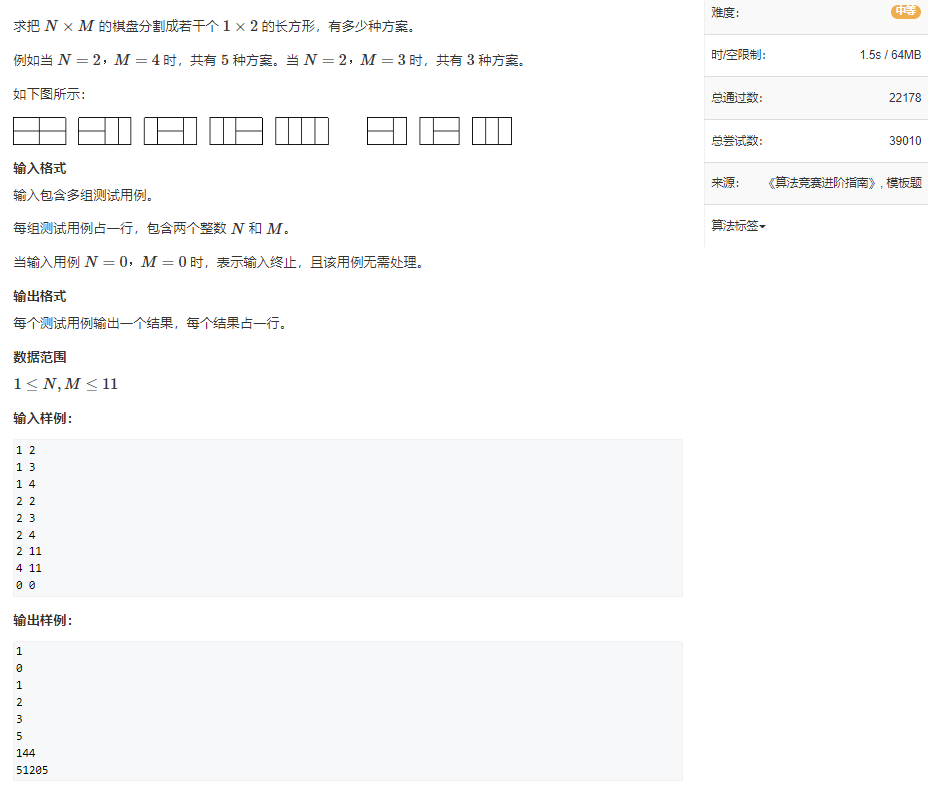
题目

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 12, M = 1 << N;
int st[M];
long long f[N][M];

int main()
{
    int n, m;
    while (cin >> n >> m && (n || m))
    //预处理：判断合并列的状态i是否合法
    //如果合并列的某一行是1表示横放，是0表示竖放
    //如果合并列不存在连续的奇数个0，即为合法状态
    
    {        
        for (int i = 0; i < 1 << n; i ++)
        {
            st[i] = true;
            int cnt =  0;   //记录合并列中连续0的个数
            for (int j = 0; j < n; j ++)
                if (i >> j & 1)  //如果是1
                {
                   if (cnt & 1) st[i] = false;  //如果连续的0个数为奇数，则记录i不合法
                   cnt = 0;
                }
                else cnt ++;                   //如果是0，记录0的个数
                
            if (cnt & 1) st[i] = false;       //处理高位0的个数
        }
        
        //状态计算
        memset(f, 0, sizeof(f));
        f[0][0] = 1;                            //第0列不横放是一种合法的方案
        for (int i = 1; i <= m; i ++)           //阶段：枚举列
            for (int j = 0; j < 1 << n; j ++)   //状态：枚举第i列的状态
                for (int k = 0; k < 1 << n; k++)//状态：枚举第i-1列的状态
                    //俩列状态兼容：不出现重叠，不出现连续的奇数个0
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];
        cout << f[m][0] << endl;               //第m列不横放即为答案
    }
    return 0;
}