本文通过数学建模分析，提出了一种新的运动辅助步态识别方法，并引入了一种视角感知的嵌入方法，旨在减少视角差异带来的识别误差。实验结果证明了该方法的有效性。
目录
1. 论文&代码源
《Lagrange Motion Analysis and View Embeddings for Improved Gait Recognition》
论文地址：https://ieeexplore.ieee.org/document/9879229
代码下载地址： https://github.com/ctrasd/LagrangeGait
2. 论文亮点
在本文中，通过数学建模分析，作者认为只使用一阶时间信息是很难进行步态识别的，为了有效地对人的行走模式进行建模，二阶运动特征是不容忽视的。
为了验证上述观点，作者提出了一种新的运动辅助步态识别方法，以进一步减少视角差异带来的识别误差，同时引入了一种视角感知的嵌入方法，其能够产生一个多分支框架，该框架结合了剪影序列的视图、外观和内在运动。
实验结果表明，本文所提出的模型可以有效地缩小因视角差异引起的类内误差。
注意：本文中， d x d t \frac {\text d x}{\text d t} dtdx为一阶运动特征； d 2 θ d t 2 \frac {\text d^2 \theta}{\text d t^2} dt2d2θ为二阶运动特征。
1) 通过拉格朗日方程对人体进行建模：
通过拉格朗日方程（组）对人类行走过程进行建模，并得出结论：除了一阶运动特征外，我们还需要使用二阶运动特征来表示步态；
2) 提出二阶运动提取模块：
二阶运动提取模块能够提取高层特征图上的特征；
3) 引入一种新的轻量级视图嵌入模块：
引入一种新的、轻量级的视图嵌入模块，能够减少因视角变化引起的识别误差；
4) 实验结果可视化：
将所提出的方法应用于公共数据集，验证了方法的有效性，并进行了一些可视化的严谨，以进一步证明方法的正确性。
3. 模型结构
3.1 建模思路
现阶段步态识别的最优方法虽然能够取得很高的识别精度，但是我们很难确定它究竟是依赖于人体形状还是“步态”进行识别的。基于这一猜想，作者提出了使用拉格朗日方程来分析人类的行走模式。
3.2 建立拉格朗日方程
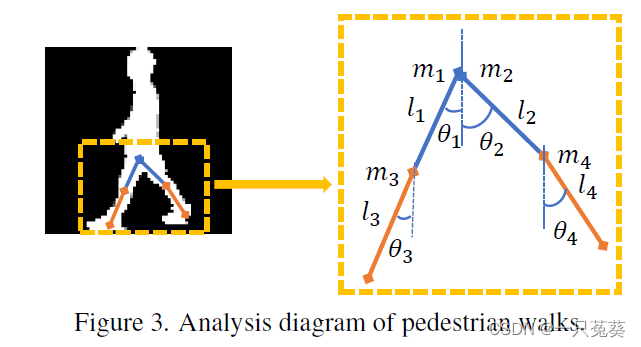
如上图所示，假设人的大腿和小腿是刚性连接的，从而对其进行机械结构的建模。
两条大腿和小腿的长度和质量分别用
l
1
l_1
l1,
l
2
l_2
l2,
m
1
m_1
m1,
m
2
m_2
m2和
l
3
l_3
l3,
l
4
l_4
l4,
m
3
m_3
m3,
m
4
m_4
m4表示；
θ
i
\theta _i
θi表示（大/小）腿与水平线之间的夹角；假设人是以小距离
x
x
x水平向前运动。
首先可以得到动能方程：
T
=
1
2
(
m
1
+
m
2
+
m
3
+
m
4
)
(
d
x
d
t
)
2
+
1
6
(
m
1
l
1
2
(
d
θ
1
d
t
)
2
+
m
2
l
2
2
(
d
θ
2
d
t
)
2
+
m
3
l
3
2
(
d
θ
3
d
t
)
2
+
m
4
l
4
2
(
d
θ
4
d
t
)
2
)
(
1
)
T = \frac 12(m_1 + m_2 + m_3 + m_4)(\frac {\mathrm d x}{\mathrm dt})^2 + \frac 16(m_1 l_1^2(\frac{\mathrm d \theta_1}{\mathrm dt})^2\\+ m_2 l_2^2(\frac{\mathrm d \theta_2}{\text dt})^2+ m_3 l_3^2(\frac{\mathrm d \theta_3}{\mathrm dt})^2+ m_4 l_4^2(\frac{\mathrm d \theta_4}{\mathrm dt})^2) \qquad(1)
T=21(m1+m2+m3+m4)(dtdx)2+61(m1l12(dtdθ1)2+m2l22(dtdθ2)2+m3l32(dtdθ3)2+m4l42(dtdθ4)2)(1)
势能方程：
V
=
−
1
2
m
1
g
l
1
c
o
s
θ
1
−
m
3
g
(
l
1
c
o
s
θ
1
+
l
3
2
c
o
s
θ
3
)
−
1
2
m
2
g
l
2
c
o
s
θ
2
−
m
4
g
(
l
2
c
o
s
θ
2
+
l
4
2
c
o
s
θ
4
)
(
2
)
V = -\frac 12 m_1gl_1 \mathrm {cos} \theta_1 - m_3g(l_1 \mathrm {cos} \theta_1 + \frac{l_3}2 \mathrm{cos} \theta_3) \\ -\frac 12 m_2gl_2 \mathrm {cos} \theta_2 - m_4g(l_2 \mathrm {cos} \theta_2 + \frac{l_4}2 \mathrm{cos} \theta_4) \qquad(2)
V=−21m1gl1cosθ1−m3g(l1cosθ1+2l3cosθ3)−21m2gl2cosθ2−m4g(l2cosθ2+2l4cosθ4)(2)
然后凑出拉格朗日方程：
（说实话，从上面两个等式我怎么凑也没能凑出来下面的拉格朗日方程组，不知道是前面的列错了，还是后面的方程组是错的，，，这一部分有待继续研究。。。。）
{
(
m
1
+
m
2
+
m
3
+
m
4
)
d
2
x
d
t
2
=
Q
0
1
3
m
1
l
1
2
d
2
θ
1
d
t
2
−
1
2
(
m
1
+
m
3
)
g
l
1
s
i
n
θ
1
d
θ
1
d
t
=
Q
1
1
3
m
2
l
2
2
d
2
θ
2
d
t
2
−
1
2
(
m
2
+
m
4
)
g
l
1
s
i
n
θ
2
d
θ
2
d
t
=
Q
2
(
3
)
1
3
m
3
l
3
2
d
2
θ
3
d
t
2
−
1
2
m
3
g
l
3
s
i
n
θ
3
d
θ
3
d
t
=
Q
3
1
3
m
4
l
4
2
d
2
θ
4
d
t
2
−
1
2
m
4
g
l
4
s
i
n
θ
4
d
θ
4
d
t
=
Q
4
\begin{cases} (m_1 +m_2 +m_3 + m_4)\frac{\mathrm d^2x}{\mathrm d t^2} =Q_0\\ \displaystyle \frac 13 m_1 l_1^2 \frac {\mathrm d^2 \theta _1}{\mathrm d t^2} -\frac12(m_1 +m_3)gl_1 \mathrm {sin} \theta _1 \frac {\mathrm d \theta _1}{\mathrm d t} = Q_1 \\ \displaystyle \frac 13 m_2 l_2^2 \frac {\mathrm d^2 \theta _2}{\mathrm d t^2} -\frac12(m_2 +m_4)gl_1 \mathrm {sin} \theta _2 \frac {\mathrm d \theta _2}{\mathrm d t} = Q_2\qquad(3) \\ \displaystyle \frac 13 m_3 l_3^2 \frac {\mathrm d^2 \theta _3}{\mathrm d t^2} -\frac12 m_3 gl_3 \mathrm {sin} \theta _3 \frac {\mathrm d \theta _3}{\mathrm d t} = Q_3 \\ \displaystyle \frac 13 m_4 l_4^2 \frac {\mathrm d^2 \theta _4}{\mathrm d t^2} -\frac12 m_4 gl_4 \mathrm {sin} \theta _4 \frac {\mathrm d \theta _4}{\mathrm d t} = Q_4 \\ \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(m1+m2+m3+m4)dt2d2x=Q031m1l12dt2d2θ1−21(m1+m3)gl1sinθ1dtdθ1=Q131m2l22dt2d2θ2−21(m2+m4)gl1sinθ2dtdθ2=Q2(3)31m3l32dt2d2θ3−21m3gl3sinθ3dtdθ3=Q331m4l42dt2d2θ4−21m4gl4sinθ4dtdθ4=Q4
其中， Q 0 Q_0 Q0, Q 1 Q_1 Q1, Q 2 Q_2 Q2, Q 3 Q_3 Q3, Q 4 Q_4 Q4表示的是广义力，广义力是来自人体肌肉的力和阻力，这些力是人运动的本质，并且在一个步态周期内连续变化。
3.3 网络结构
作者提出疑问：
我们已知的是3D CNN可以提取时间信息，但是很难证明级联后的3D CNN是否可以进一步提取二阶运动信息，并且很难知道3D CNN是在提取运动信息，还是仅仅对特征图进行求和。
所以作者设计了一个模块，利用光流估计中使用的方法提取二阶运动特征，与3D CNN相比，这一方法可以明确地提取相邻帧之间的运动（从而进一步分析）。
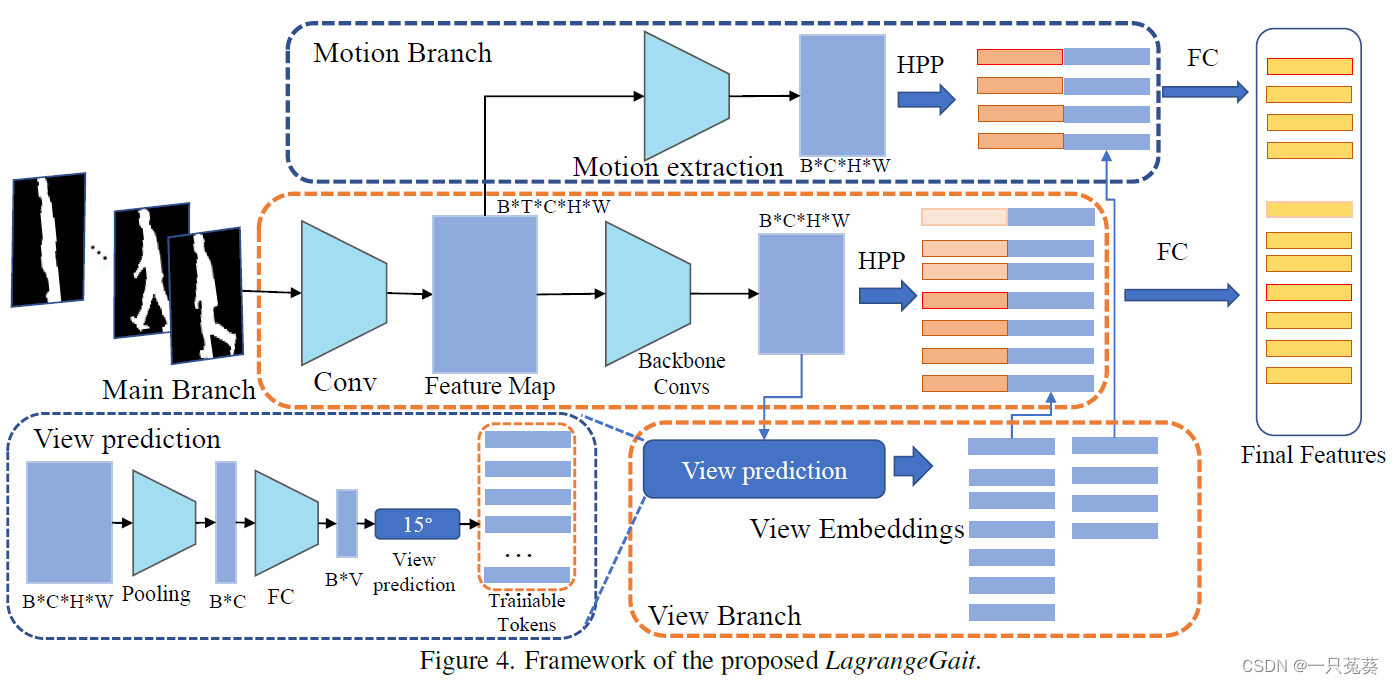
作者提出了一个名为LagrangeGait的网络模型，该网络的框架由三个分支组成。
顶层分支是运动分支，根据前述列出的拉格朗日方程，提取二阶运动特征；中间分支是提取外观特征的主干分支，借鉴的是GaitSet或GaitGL等骨架网络，在这一分支中浅层提取出的特征图被用于运动（顶层）分支；底层分支为视觉分支，负责预测输入剪影序列的视图，并产生可训练的视图嵌入模块。
给定一个步态剪影序列，表示为 I = { I 1 , I 2 , . . . , I T } \pmb I = \{ \pmb I_1, \pmb I_2, ..., \pmb I_T \} III={III1,III2,...,IIIT}，其中 T T T为序列长度。
主干分支提取的浅层特征图为 X o r i g i n = [ X 1 , X 2 , . . . , X t ] \pmb X_{origin} = [\pmb X_1, \pmb X_2, ..., \pmb X_t] XXXorigin=[XXX1,XXX2,...,XXXt]，其中 X i ∈ R C × H × W \pmb X_i \in \Bbb R^{C \times H \times W} XXXi∈RC×H×W， X o r i g i n ∈ R t × C × H × W \pmb X_{origin} \in \Bbb R^{t \times C \times H \times W} XXXorigin∈Rt×C×H×W， t t t是池化后特征图在时间维度上的长度。
随后，
X
o
r
i
g
i
n
\pmb X_{origin}
XXXorigin被送入不同的分支：
X
o
r
i
g
i
n
=
F
3
d
(
I
)
X
m
o
t
i
o
n
=
F
m
o
t
i
o
n
(
X
o
r
i
g
i
n
)
X
a
p
p
e
a
r
a
n
c
e
=
F
b
a
c
k
b
o
n
e
(
X
o
r
i
g
i
n
)
f
v
i
e
w
=
F
v
i
e
w
(
X
a
p
p
e
a
r
a
n
c
e
)
\pmb X_{origin} = F_{3d}(\pmb I)\\ \pmb X_{motion} = F_{motion}(\pmb X_{origin})\\ \pmb X_{appearance} = F_{backbone}(\pmb X_{origin})\\ \pmb f_{view} = F_{view}(\pmb X_{appearance})
XXXorigin=F3d(III)XXXmotion=Fmotion(XXXorigin)XXXappearance=Fbackbone(XXXorigin)fffview=Fview(XXXappearance)其中，
X
m
o
t
i
o
n
,
X
a
p
p
e
a
r
a
n
c
e
∈
R
C
2
×
H
×
W
\pmb X_{motion}, \pmb X_{appearance} \in \Bbb R^{C_2 \times H \times W}
XXXmotion,XXXappearance∈RC2×H×W,
f
v
i
e
w
∈
R
C
3
\pmb f_{view} \in \Bbb R^{C_3}
fffview∈RC3以及
F
m
o
t
i
o
n
,
F
b
a
c
k
b
o
n
e
,
F
v
i
e
w
F_{motion}, F_{backbone}, F_{view}
Fmotion,Fbackbone,Fview分别与上述三个分支相对应。
然后，对序列视角进行预测，并融合到 X m o t i o n \pmb X_{motion} XXXmotion和 X a p p e a r a n c e \pmb X_{appearance} XXXappearance中： p ^ = F p r e d i c t ( f v i e w ) f m o t i o n = F f u s i o n 1 ( X m o t i o n , p ^ ) f a p p e a r a n c e = F f u s i o n 2 ( X a p p e a r a n c e , p ^ ) \hat p = F_{predict}(\pmb f_{view})\\ \pmb f_{motion} = F_{fusion_1}(\pmb X_{motion},\hat p)\\ \pmb f_{appearance} = F_{fusion_2}(\pmb X_{appearance}, \hat p) p^=Fpredict(fffview)fffmotion=Ffusion1(XXXmotion,p^)fffappearance=Ffusion2(XXXappearance,p^)其中， p ^ ∈ R M \hat p \in \Bbb R^M p^∈RM是预测视角， M M M是离散视图的个数； f m o t i o n \pmb f_{motion} fffmotion和 f a p p e a r a n c e \pmb f_{appearance} fffappearance分别是最终得到的运动特征和外观特征， f m o t i o n ∈ R n m o t i o n × C 3 , f a p p e a r a n c e ∈ R n a p p e a r a n c e × C 3 \pmb f_{motion} \in \Bbb R^{n_{motion} \times C_3}, f_{appearance} \in \Bbb R^{n_{appearance} \times C_3} fffmotion∈Rnmotion×C3,fappearance∈Rnappearance×C3，其中 n m o t i o n , n a p p e a r a n c e n_{motion} , n_{appearance} nmotion,nappearance是使用HPP模块对运动特征图和外观特征图进行切片的条数， C 3 C_3 C3是两个特征图的通道数（是相等的）。
最终用于步态识别的特征为：
f
f
i
n
a
l
=
[
f
m
o
t
i
o
n
;
f
a
p
p
e
a
r
a
n
c
e
]
(
4
)
\pmb f_{final} = [\pmb f_{motion}; \pmb f_{appearance}] \qquad(4)
ffffinal=[fffmotion;fffappearance](4)
上述方程的具体运算过程将在下文中进行详细解释。
3.3.1 运动分支（Motion Branch）
一阶特征提取层使用三维卷积，二阶特征提取参考RAFT光流法【RAFT: Recurrent All-Pairs Field Transforms for Optical Flow】的结构（光流法的介绍可以参考这一篇博客：【入门向】光流法（optical flow）基本原理+深度学习中的应用【FlowNet】【RAFT】），并使用相邻帧响应关系： X 0 = F Q ( X o r i g i n , i ) X 1 = F K ( X o r i g i n , i + 1 ) A t t ( X 0 , X 1 ) = S o f t m a x ( X 0 T X 1 ) \pmb X_0 = F_Q(\pmb X_{origin, i})\\ \pmb X_1 = F_K(\pmb X_{origin, i+1})\\ Att(\pmb X_0, \pmb X_1) = Softmax(\pmb X_0^T\pmb X_1) XXX0=FQ(XXXorigin,i)XXX1=FK(XXXorigin,i+1)Att(XXX0,XXX1)=Softmax(XXX0TXXX1)其中， F Q F_Q FQ和 F K F_K FK是核为 1 × 1 1 \times 1 1×1的卷积层组合，进行维度合并； A t t ( X 0 , X 1 ) ∈ R H W × H W Att(\pmb X_0, \pmb X_1) \in \Bbb R^{HW \times HW} Att(XXX0,XXX1)∈RHW×HW。
随后，相关图被重塑为 C o r ( X 0 , X 1 ) ∈ R H × W × H W Cor(\pmb X_0, \pmb X_1) \in \Bbb R^{H \times W \times HW} Cor(XXX0,XXX1)∈RH×W×HW。
因为我们已经假设在一帧的时间内，人体的移动是很微小的，那么对于 X o r i g i n , i \pmb X_{origin, i} XXXorigin,i中的任一像素点 x = ( u , v ) \pmb x = (u, v) xxx=(u,v)，在 X o r i g i n , i + 1 \pmb X_{origin, i+1} XXXorigin,i+1中对应的像素点为 x ′ = ( u + f 1 ( u ) , v + f 1 ( v ) ) \pmb x' = (u+f^1(u), v+f^1(v)) xxx′=(u+f1(u),v+f1(v))，采样范围为： N ( x ) r = { x + d x ∣ d x ∈ Z 2 , ∣ ∣ d x ∣ ∣ 1 ≤ r } N(x)_r = \{\pmb x + \pmb{dx}|\pmb {dx}\in \Bbb Z^2,||\pmb{dx}||_1 \le r \} N(x)r={xxx+dxdxdx∣dxdxdx∈Z2,∣∣dxdxdx∣∣1≤r}其中， d x \pmb{dx} dxdxdx是采样偏移量， r r r是采样半径。
对于 C o r ( X 0 , X 1 ) Cor(\pmb X_0, \pmb X_1) Cor(XXX0,XXX1)上的每一个像素点 x \pmb x xxx，我们根据 N ( x ) r N(x)_r N(x)r定义的公式进行采样，可以得到 X c o r r , i ′ ∈ R H × W × ( 2 r + 1 ) 2 \pmb X_{corr,i}' \in \Bbb R^{H \times W \times (2r+1)^2} XXXcorr,i′∈RH×W×(2r+1)2，然后对通道的表示位置进行交换，得到 X c o r r , i ∈ R ( 2 r + 1 ) 2 × H × W \pmb X_{corr,i} \in \Bbb R^{(2r+1)^2 \times H \times W} XXXcorr,i∈R(2r+1)2×H×W
最后，二阶特征图在时间维度上进行整合，得到一个特征图的序列： X c o r r = [ X c o r r , 1 ; X c o r r , 2 ; . . . ; X c o r r , t − 1 ] X_{corr} = [X_{corr,1}; X_{corr,2}; ...; X_{corr,t-1}] Xcorr=[Xcorr,1;Xcorr,2;...;Xcorr,t−1]其中 X c o r r ∈ R ( 2 r + 1 ) 2 × t − 1 × H × W X_{corr} \in \Bbb R^{(2r+1)^2 \times {t-1} \times H \times W} Xcorr∈R(2r+1)2×t−1×H×W。
然后，使用三维卷积得到运动特征： X m o t i o n = F 3 d c o n v ( X c o r r ) ( 5 ) \pmb X_{motion} = F_{3dconv}(X_{corr}) \qquad(5) XXXmotion=F3dconv(Xcorr)(5)其中， F 3 d c o n v F_{3dconv} F3dconv的卷积核大小为 3 × 3 × 3 3 \times 3 \times 3 3×3×3， X m o t i o n ∈ R C 2 × T × H × W \pmb X_{motion} \in \Bbb R^{C2 \times T \times H \times W} XXXmotion∈RC2×T×H×W。
3.3.2 视图嵌入分支（View Embedding）
对于现有的步态识别模型，很少有考虑到视图本身的方法，本文作者提出了一种更轻量级的视图嵌入（融合）方法。
首先计算输入特征图 X o r i g i n \pmb X_{origin} XXXorigin的视图特征： X a p p e a r a n c e = P M a x ( X o r i g i n ) f v i e w = P G l o b a l _ A v g ( X a p p e a r a n c e ) \pmb X_{appearance} = P_{Max}(\pmb X_{origin})\\ \pmb f_{view} = P_{Global\_Avg}(\pmb X_{appearance}) XXXappearance=PMax(XXXorigin)fffview=PGlobal_Avg(XXXappearance)其中， P M a x P_{Max} PMax是时间维度上的最大池化， P G l o b a l _ A v g P_{Global\_Avg} PGlobal_Avg是全局平均池化。
然后，预测的视角可以用下列方程进行计算： p ^ = W v i e w f v i e w + B v i e w y ^ = argmax p i ^ \hat p = W_{view} \pmb f_{view} +B_{view} \\ \hat y = \text{arg} \text{max}\hat{p_i} p^=Wviewfffview+Bviewy^=argmaxpi^其中， W v i e w ∈ R M × C 2 W_{view} \in \Bbb R^{M \times C_2} Wview∈RM×C2和 B v i e w B_{view} Bview分别是全连接层的权重和偏置；视图预测结果 y ^ ∈ { 0 , 1 , 2 , . . . , M − 1 } \hat y \in \{0, 1, 2, ..., M-1\} y^∈{0,1,2,...,M−1}； M M M是视角数量，对于CASIA-B数据集 M = 11 M=11 M=11，对于OU-MVLP数据集 M = 14 M=14 M=14。
argmax是求出使因变量为最大值时自变量的值（集合），这里返回的是自变量的索引值。
对于每一个离散视角 y ^ \hat y y^，将训练两个嵌入 E m , y ^ ∈ C 0 E_{m,\hat y} \in \Bbb C_0 Em,y^∈C0和 E a , y ^ ∈ C 0 E_{a,\hat y} \in \Bbb C_0 Ea,y^∈C0分别融合进运动和外观特征，并应用于HPP模块。
3.3.3 水平金字塔池化（HPP）
在步态识别中，水平金字塔池化（HPP）已经被广泛应用，本文除了对外观使用HPP之外，还对运动特征图做了同样的池化操作，在对两者进行池化结束后，与前面视角嵌入结果相连接，得到最终的特征投影。
对于HPP后得到的外观特征图表示为 f a p p , 1 , f a p p , 2 , . . . , f a p p , n \pmb f_{app,1}, \pmb f_{app,2}, ..., \pmb f_{app,n} fffapp,1,fffapp,2,...,fffapp,n其中， f a p p , i ∈ R C 2 \pmb f_{app,i} \in \Bbb R^{C_2} fffapp,i∈RC2， n n n是被分割出的条数，对于运动分支和外观分支，条数分别是 n m o t i o n n_{motion} nmotion和 n a p p e a r a n c e n_{appearance} nappearance。
作者原文这部分的
F
f
u
s
i
o
n
1
F_{fusion_1}
Ffusion1和
F
f
u
s
i
o
n
2
F_{fusion_2}
Ffusion2搞混了。。
假设
X
m
o
t
i
o
n
\pmb X_{motion}
XXXmotion是
z
z
z，那么
F
f
u
s
i
o
n
1
F_{fusion_1}
Ffusion1可以用下式进行计算：
f
m
v
,
i
=
[
f
m
o
t
i
o
n
,
i
;
E
m
,
z
]
f
f
i
n
a
l
m
,
i
=
W
p
f
m
v
,
i
,
i
=
1
,
2
,
.
.
.
,
n
m
o
t
i
o
n
f
m
o
t
i
o
n
=
[
f
f
i
n
a
l
m
,
1
,
f
f
i
n
a
l
m
,
2
,
.
.
.
,
f
f
i
n
a
l
m
,
n
m
o
t
i
o
n
]
\pmb f_{mv,i} = [\pmb f_{motion,i};E_{m,z}]\\ \pmb f_{finalm,i} = W_p \pmb f_{mv,i}, \space i=1, 2, ..., n_{motion} \\ \pmb f_{motion} = [\pmb f_{finalm,1}, \pmb f_{finalm,2}, ..., \pmb f_{finalm,n_{motion}}]
fffmv,i=[fffmotion,i;Em,z]ffffinalm,i=Wpfffmv,i, i=1,2,...,nmotionfffmotion=[ffffinalm,1,ffffinalm,2,...,ffffinalm,nmotion]其中，
f
m
v
,
i
∈
R
C
2
+
C
0
\pmb f_{mv,i} \in \Bbb R^{C_2 +C_0}
fffmv,i∈RC2+C0，
f
f
i
n
a
l
m
,
i
∈
R
C
2
\pmb f_{finalm,i} \in \Bbb R^{C_2}
ffffinalm,i∈RC2，
f
m
o
t
i
o
n
∈
R
n
m
o
t
i
o
n
×
C
2
\pmb f_{motion} \in \Bbb R^{n_{motion} \times C_2}
fffmotion∈Rnmotion×C2。
对 X a p p e a r a n c e \pmb X_{appearance} XXXappearance同理。
最后得到最终特征 f f i n a l ∈ R ( n m o t i o n + n a p p e a r a n c e ) × C 2 \pmb f_{final} \in \Bbb R^{(n_{motion}+n_{appearance})\times C_2} ffffinal∈R(nmotion+nappearance)×C2。
3.3.4 损失函数
包括交叉熵损失和三元组损失，用公式分别表示为：
L
C
E
=
−
∑
i
=
1
N
∑
j
=
1
M
y
i
j
log
(
p
i
j
)
,
p
i
j
=
e
p
^
i
j
∑
j
=
1
M
e
p
^
i
j
(
6
)
\mathcal L_{CE} = -\sum_{i=1}^N \sum _{j=1}^M y_{ij}\text {log}(p_{ij}),\space p_{ij} = \frac {e^{\hat p_{ij}}}{\sum _{j=1}^M e^{\hat p_{ij}}}\qquad(6)
LCE=−i=1∑Nj=1∑Myijlog(pij), pij=∑j=1Mep^ijep^ij(6)
L
t
r
i
p
=
1
K
∑
i
=
1
K
∑
j
=
1
n
m
a
x
(
m
−
d
i
j
−
+
d
i
j
+
,
0
)
(
7
)
\mathcal L_{trip} = \frac 1K \sum _{i=1}^K \sum _{j=1}^n max(m-d_{ij}^- + d_{ij}^+,0)\qquad(7)
Ltrip=K1i=1∑Kj=1∑nmax(m−dij−+dij+,0)(7)
L
=
L
t
r
i
p
+
λ
C
E
L
C
E
(
8
)
\mathcal L = \mathcal L_{trip} + \lambda_{CE} \mathcal L_{CE}\qquad(8)
L=Ltrip+λCELCE(8)
4. 实验结果
4.1 CASIA-B
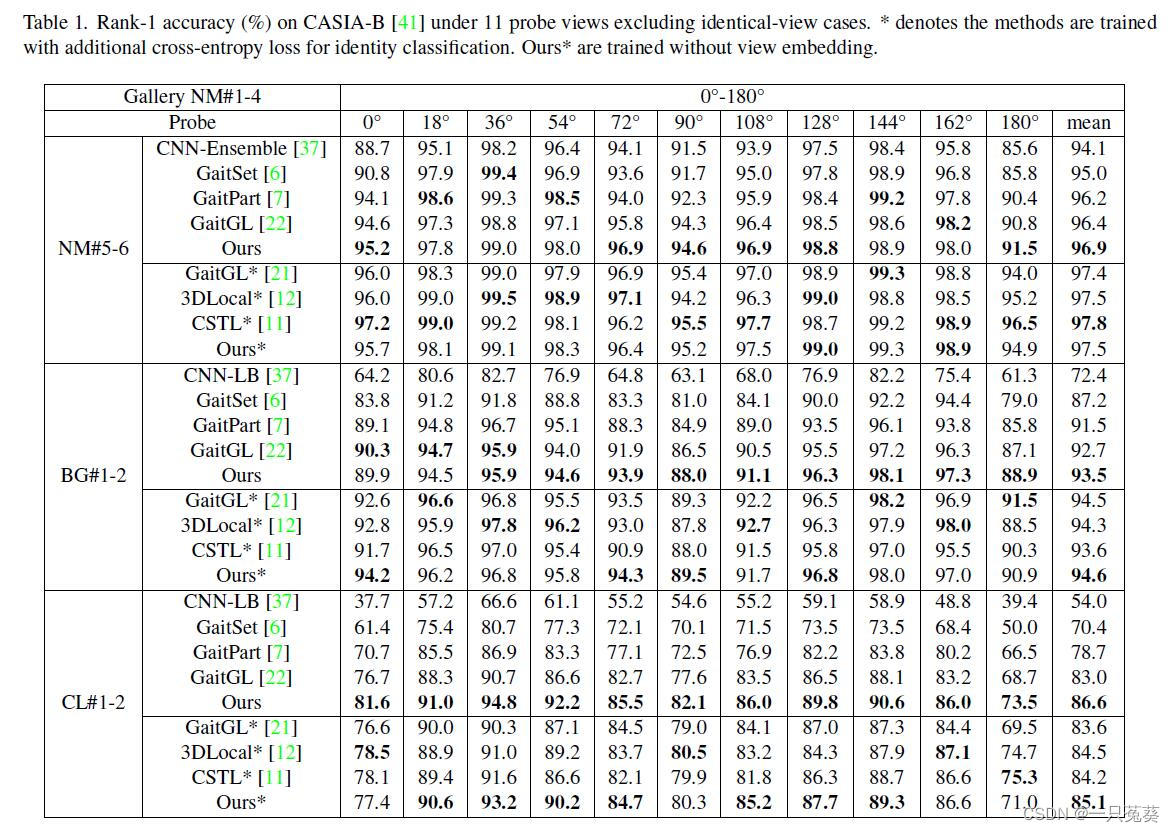
4.2 OU-MVLP
4.3 消融实验
4.4 结果可视化
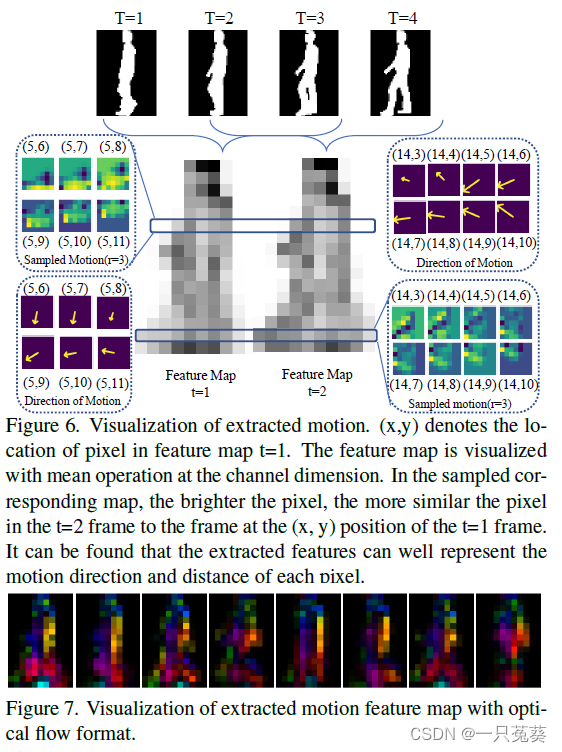
5.总结
本文首先用拉格朗日方程对人类的行走过程进行建模，并说明了二阶运动信息对于区分相似步态外观是十分必要的。基于这一结论，作者解释了为什么使用3D CNN能够取得更好地性能，并提出了一个新的二阶运动提取模块。
此外，作者提出了一个轻量级的视角嵌入模块，以减少因视角变化引起的类内误差。
最后作者期望拉格朗日步态识别框架能够为其他领域的运动分析提供新思路。
参考博客：
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
