伽罗华域（有限域）

域

域F由元素和加法、乘法两种运算组成，且每种运算下都有逆运算（减法、除法）存在。域F内同时满足加法和乘法运算的各个元素需要满足以下条件：
（1）对于加法和乘法运算，F是封闭的，即F内任意两个元素之和或之积仍在F内；
（2）对每种运算，域内元素通常满足结合律和交换律；
（3）满足通常的分配律；
（4）F内的任何元素u都有一个唯一的加法恒元0和乘法恒元1，满足以下关系：u+0=u，u x1=u。
（5）域内的每个元素u都有一个唯一的加法逆元-u，且：u+（-u）=0。当u！=0时，有一个唯一的乘法逆元u^-1，且u x （u^-1）=1.。
域内元素的个数称为域的阶，可以是有限的，也可以是无限的。

有限域

有限域以 GF（q） 表示， q 是域内的 元素个数。对任何的 q^m ，都存在一个有限域 GF（q^m） ,其中 q 是素数， m 是整数。 GF（2） 是最简单的素域，他只含有 0 和 1 表示的 0 元和 1 元。
有限域在编码理论中具有重要的地位，包括有限个元素的域成为有限域或伽罗华域，通常把有 q 个元素的有限域几位 GF（q） 。每个域中必须包含一个零元 0 和一个单位元 e ，若 q 为素数，则可构成一个由元素 {0，1，…，q-1} 组成的 q 元域 GF（q） 。对任何正整数m，都可以将 GF（q） 扩展成 GF（q^m），称之为 GF（q） 的 m 次扩域。
在有限域 GF（q）中，加法和乘法运算定义为模 q 运算，记为 mod q 。在域 GF（q） 中，满足 ne=0 的最小正整数 n 称为域的特征。域中一切非零元素的特征都等于域的特征，域的特征一定为素数。非零元素构成的乘法群的阶定义为域中该元素的级。若 a 为域 GF（q） 中的 n 级元素，则称 a 为 n 次单位原根。若某一元素 a 的级为 q-1 ，则称 a 为本院域元素合伙本原元。域的特征表明了域中加法运算的循环性，域的级表明了域中乘法运算的循环性。
二元域 GF（2）是扩域 GF（2^m） 的一个子域，类似于实数域的一个子域。有限元素的集合 GF（2^m） 只能含有 2^m 个元素，可以全部有本原元 a 的幂次和零元 0 表示，并且对乘法封闭，其约束条件为
b= 2^m-1
a^b+1=0
根据这个限制条件，任何幂次等于或超于 b 的域元素都可将为下述幂次小于 b 的元素。
A=2^m+n, B=2^m-1, C=2ⁿ+1
a^A=a^Ba^C=a^C
因此 GF（2^m） 的全部元素就可以表示为
GF（2^m） ={0， a⁰, a¹, …, a^b-1}

有限域上的运算

有限域的一个重要的性质是每个有限域 GF（q） 至少包括一个本原 a 。该元素的 q-1 次幂就是这个域的 q-1 个非零元素，也即 q-1 个非零元素可表示为 {a, a², … , a^q-2} 且互不相等，所以 aⁱa^j 的 q-1中乘积也互不相等。域中所有非零元素都可以用本原元 a 的前 q-1 个秘书来表示，即也可用他们各自的指数表示各个域元素。
在实际使用中，需要将域元素表示为便于计算机计算的形式。如下：
首先， GF（q）内各个元素可以构成 m 重的总数为 q^m 个元素，并且组成了一个 GF（q） 上的 m 维矢量空间。
其次，可以使用 GF（q） 中矢量的加减法进行矢量的相加和相减运算，并得到这个适量空间内的另一个矢量。
然后，为了进行矢量的乘法与除法，需要将矢量表示为多项式，其各项的系数于是两中的各元素相对应。与矢量相加相同，可以对所想是进行诸位相加。
最后，每个系数取自有限域 GF（q）的 m 次不可约多项式，最少有一个元素个数为 q^m 的有限域 GF（q）与其对应存在。
在运算过程中，元素的基本形式是十进制，运算过程如下：
（1）加法：将两个十进制数先转换为两个二进制数表示，然后将对应位进行异或运算，再将运算结果转换成十进制存储；
（2）乘法：把两个元素的十进制表示转换成指数形式，将指数直接相加，取模后得到乘积的指数形式，然后在转换称十进制形式存储。

有限域多项式

（1）域上多项式：系数取自域 GF（q）的多项式 f(x)。
（2）既约多项式：设 f(x) 是次数大于零的多项式，若出了常数和常数与本身的乘积以外再不能被 GF（q）上其他多项式除尽，则称 f(x) 为域 GF（q） 上的既约多项式。
（3）最小多项式：系数取自有限域 GF（q） ，且以 a 为根的所有首一多项式（即最高次数的系数为1的多项式）中，必有一个次数最低的，称之为 a 的最小多项式。
（4）本原多项式：系数取自有限域 GF（q） ，且以域 GF（q^m） 上本原域元素为根的最小多项式成为本原多项式。一个多项式是本原多项式的充要条件是：如果一个 m 阶既约多项式 f(x) 整除 xⁿ+1 的最小正整数 n 满足 n=2^m-1 ， 则该多项式是本原的。如下例所示：给定两个多项式 p1(x)=x⁴+x+1 和 p2(x)=x⁴+x³+x²+x+1， 判断多项式是否为本原多项式。
通过验证这个幂次为 m=4 的多项式是否能够整除 xⁿ+1， 但不能整除 1<=n<15 范围内的 xⁿ+1 ，就可以确定他是否为本原多项式。经反复计算， p1(x) 是本原多项式， p2(x) 不是，因为他能整除 x⁵+1。
不同 m 之对应的部分本原多项式如下所示：

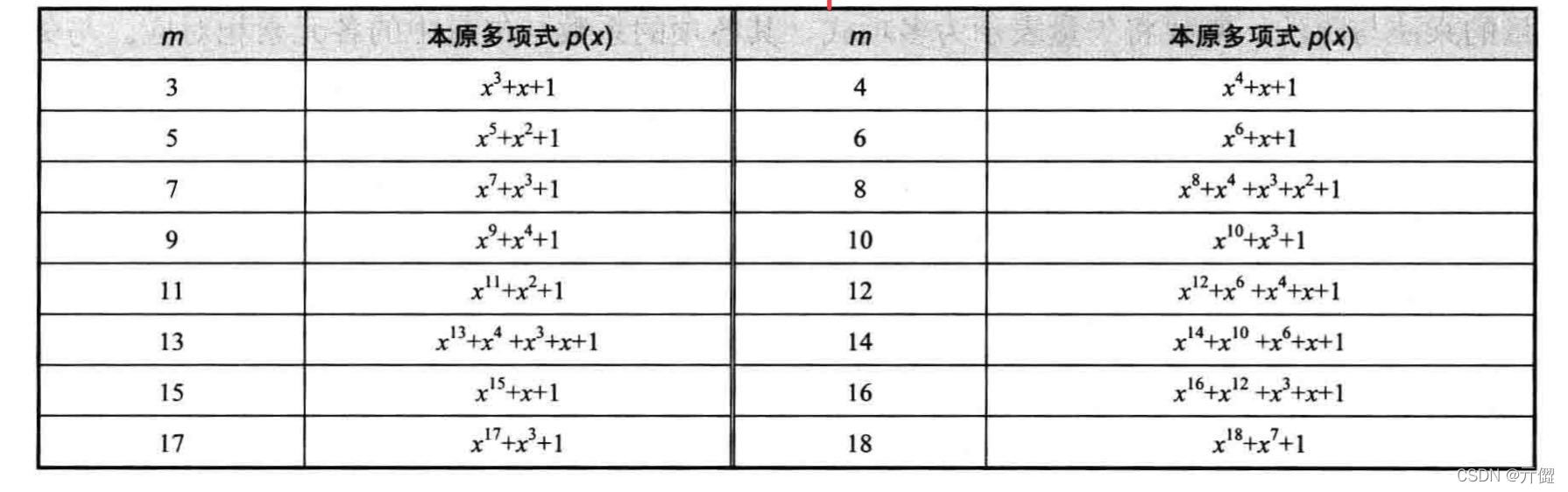
例如，假设 a 是 GF(2^m) 的本原多项式 p(x) 的根，也即 GF(2^m) 的本原元，则可以由零元和本原元 a 得到 GF(2^m) 的全部元素， m=3 时 GF(2³) 的元素如下表所示：

幂次表示	②进制表示	⑩进制表示
0	000	0
a0=1	001	1
a1=a	010	2
a2=a2	011	3
a3=a+1	100	4
a4=a2+a	101	5
a5=a2+a+1	110	6
a6=a2+1	111	7

对上述例子进行详细说明如下：
当 m=3 是，其本原多项式可从上上表中获知为 p(x)=x³+x+1，所以由 p(x) 所定义的有限域中包含了 2^m=2³=8 个元素。求解 p(x) 的根，即找到使 p(x)=0 的 x 。因为 p(0)=p(1)=1 （运用模2运算），所以二进制数 0 和 1 都不是 p(x) 的根。由基本代数学理论可知，次数为 m 的多项式必然有 m 个根。对于 m=3，p(x)=0 有3个根，这3个根不可能位于与 p(x) 系数相同的有限域中，而是位于扩展域 GF(2³) 中。用扩域的元素 a 来定义多项式 p(x) 的根，可写成 p(a)=0 ，即
a³+a+1=0 ——> a³=a+1
这意味着 a³ 可以表示更低阶的 a 项的加权和（模2加法运算等价于模2减法运算）。类似的，有：
a⁴=a x a³=a x (a+1) =a²+a
a⁵=a x a⁴=a x (a²+a)=a³+a²=a²+a+1
…
从而有限域 GF(2³) 的全部元素为
GF(2³) ={0，1，a， a²， a³ ， a⁴， a⁵， a⁶}
我们可以通过穷举来确定本原多项式的根，由于仅有 p(a)=p(a²)=p(a⁴)=0 ，因此， p(x) 的根为 a、a²、a⁴。
另外， GF(2^m) 的每个元素的最小多项式 m(x) 可以通过多项式分解得到。仍以 GF(2³) 为例进行说明。对于 GF(2³) ，p=2，m=3， 因此，对 x⁷+1 进行分解，我们可以得到
x⁷+1 =(x+1)(x³+x+1)(x³+x²+1)
而 GF(2³) 的所有非0元素为
{1，a， a²， a³ ， a⁴， a⁵， a⁶}={1，a，a²，a+1，a²+a，a²+a+1，a²+1}
在 GF(2³) 上，有
x³+x+1=(x+a)(x+a²)(x+a²+a)
x³+x²+1=(x+a+1)(x+a²+1)(x+a²+a+1)
可以将上述分解式写为：
x⁷+1=(x+1)(x+a)(x+a²)(x+a²+a)(x+a+1)(x+a²+1)(x+a²+a+1)
=(x+1)[(x+a)(x+a²)(x+a²+a)][(x+a+1)(x+a²+1)(x+a²+a+1)]*
由此，可得到每个根的最小多项式，如下表所示。