Efficient Fully Homomorphic Encryption from (Standard) LWE 论文理解

Introduction

    第一段简介了Gentry的论文贡献。

    第二段说明Gentry的方案是未经测试的新假设，本论文旨在将完全同态加密置于标准、经过充分研究的假设之上。

    Gentry的结构（所谓的“somewhat”的同态加密方案）的主要组成部分是基于理想格的困难问题（最坏情况，量子）。尽管晶格已成为密码学的标准内容，并且对晶格问题的研究相对较深入，但是理想晶格是我们相对了解甚少的特殊品种。 理想是用于构建完全同态加密的自然数学对象，因为它们本身支持加法和乘法（而晶格仅在加法下闭合）。实际上，所有后序的全同态加密思想的构造都以明确的方式依赖于各种环。我们的第一个贡献是构建“somewhat“全同态加密方案，其安全性完全取决于任意格上标准问题（最坏情况，经典）的硬度。

    其次，为了实现全同态，Gentry必须经历一个所谓的“挤压步骤”，这迫使他做出了另一个非常强的困难假设，即（平均情况）的稀疏子和的困难问题。仿佛是凭一种奇怪的自然法则，所有后续解决方案都遇到了与Gentry从“某种”加密到完全同态加密一样的困难，并且它们都依靠相同的稀疏子集和假设来克服这一困难。该附加假设被认为是主要警告Gentry解决方案的取消和删除可能是完全同态加密方案设计中的主要开放问题。 我们的第二个贡献是消除了这样做的必要性附加假设。简而言之，我们构建了一个完全同态的加密方案，其安全性完全基于在最坏情况下解决标准格问题的经典难度。解决方案基于错误学习（LWE）假设，已知该假设至少与解决一般格中的难题一样困难。 因此，我们的解决方案不直接依赖于格并且很自然地理解和实施。

    为了实现我们的目标，我们偏离了两个范式，该范式统治了（少数）候选完全同态加密方案的设计

    1.我们介绍了双线性化技术，并展示了如何使用它来获得某种同态加密，而无需对理想情况下的硬度进行假设。

    2.提出了一种降模技术，该技术将我们“somewhat”同态方案变成了完全同态的方案，而无需人工挤压步骤和稀疏子集和困难假设。

 

1.1 双线性：不需要理想化的Somewhat 全同态加密

    Gentry的构建起点是“某种”同态加密方案。 对于C类电路，C同态方案是一种允许评估C类中任何电路的方案。Gentry工作中简单但引人注目的观察结果是，如果C（同态）解密电路（略有增强） 方案驻留在C中，则可以将方案进行转换（或“自举”）为完全同态的加密方案。

    事实证明，可以评估加法和乘法运算3的非平凡数量的加密方案已经相当困难了（即使不需要自举）。Gentry针对此问题的解决方案基于环中理想的代数概念。在非常高的层次上，该消息被认为是环元素，密文是被某些“噪声”掩盖的消息。这种想法的新颖之处在于，噪声本身属于理想。因此，密文的形式为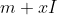（对于环中的某些x）。立即观察到该方案是相加同态的；实际上，我们在本文中考虑的所有方案都是如此。理想I具有两个主要属性：首先，假定理想中的随机元素会“掩盖”消息；第二，可能会产生一个秘密陷门，“消灭”理想，即实施变换。
第一个属性保证安全性，而第二个属性则允许倍增密文。假设和分别是和的加密，

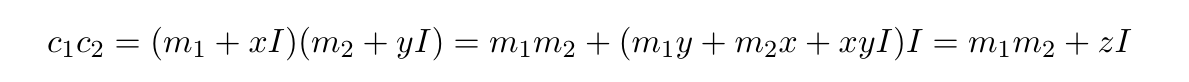
     解密时，理想被消灭，乘积得以生存。 因此，根据需要，实际上是对的加密。 根据第一个特性，这种精美的解决方案需要困难对某些环的理想的假设。 Gentry的原始工作依赖于理想格上的困难假设，而van Dijk，Gentry，Halevi和Vaikuntanathan [DGHV10]提出了一种不同的实例，该实例考虑了关于整数的理想情况。

    我们有些同态的方案是基于Regev [Reg05]首先提出的“错误学习”（LWE）问题的难度。 LWE假设指出，如果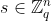是n维的“秘密”向量，则s的系数的任何“有噪声”随机线性组合的多项式都无法与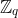中的均匀随机元素在计算上区分开。 数学上

    

其中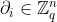，和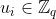都是随机数。而“噪声” 是从噪声分布中采样的，该噪声分布输出的数字远小于q（例如，离散高斯分布
超过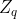且标准偏差较小）。 

     LWE假设与理想无关，实际上，LWE问题至少与在任何格中找到短向量一样困难，从Regev [Reg05]和Peikert [Pei09]的最坏情况到平均情况的减少如下 。 如前所述，与理想格上的相应问题相比，我们对晶格问题的复杂性有了更好的理解（由于[LLL82，Ajt98，Mic00]和许多其他问题）。 尤其是，尽管付出了巨大的努力，但解决LWE问题的最著名算法的时间却在维度n上几乎成指数增长。 5个事实证明，LWE假设特别适合于构建简单，高效和高表达的加密方案（例如[Reg05，GPV08，AGV09，ACPS09，CHKP10，ABB10]等）。 我们从LWE构建的完全同态加密方案可能证明了其强大和优雅。

    构建安全性基于LWE假设的（秘密密钥）加密方案非常简单。 为了使用密钥s∈Z加密比特m∈{0,1}，我们选择一个随机向量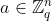和一个“噪声” e并输出密文。

    

    解密中的主要观察结果是两个“掩码”（即秘密掩码<a，s>和“偶数掩码” 2e）互不干扰。 也就是说，一个人可以通过消灭两个掩码来依次解密该密文：首先是解密算法重新计算掩码<a，s>并从b中减去它，得到2e + m（mod q）。 由于e << q，则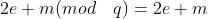。 现在，去除偶数掩码很容易，只需计算。

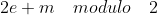    正如我们将在下面看到的那样，该方案是加法同态的，但是乘法提出了一个棘手的问题。 实际上，Gentry，Halevi和Vaikuntanathan [GHV10b]的最新工作表明，该方案（该方案的一个微小变体）仅支持单个同态乘法，但以对密文的巨大破坏为代价，这使得进一步发展变得不可能

    为了更好地理解该方案的同态性质，让我们将焦点从加密算法中移开，转移至解密算法。给定密文，考虑到符号线性函数定义为：