人工智能知识分享第十天-机器学习_朴素贝叶斯

朴素贝叶斯

朴素贝叶斯介绍

常见的概率公式

条件概率： 表示事件A在另外一个事件B已经发生条件下的发生概率，P(A|B)

在女神喜欢的条件下，职业是程序员的概率？

1. 女神喜欢条件下，有 2、3、4、7 共 4 个样本
2. 4 个样本中，有程序员 3、4 共 2 个样本
3. 则 P(程序员|喜欢) = 2/4 = 0.5

联合概率： 表示多个条件同时成立的概率，P(AB) = P(A) P(B|A)
特征条件独立性假设：P(AB) = P(A) P(B)

职业是程序员并且体型匀称的概率？

在女神喜欢的条件下，职业是程序员的概率？

1. 女神喜欢条件下，有 2、3、4、7 共 4 个样本
2. 4 个样本中，有程序员 3、4 共 2 个样本
3. 则 P(程序员|喜欢) = 2/4 = 0.5
4. 联合概率： 表示多个条件同时成立的概率，P(AB) = P(A) P(B|A)
   特征条件独立性假设：P(AB) = P(A) P(B)

职业是程序员并且体型匀称的概率？

1. 数据集中，共有 7 个样本
2. 职业是程序员有 1、3、4 共 3 个样本，则其概率为：3/7
3. 在职业是程序员，体型是匀称有 3 共 1 个样本，则其概率为：1/3
4. 则即是程序员又体型匀称的概率为：3/7 * 1/3 = 1/7

联合概率 + 条件概率：

在女神喜欢的条件下，职业是程序员、体重超重的概率？ P(AB|C) = P(A|C) P(B|AC)

1. 在女神喜欢的条件下，有 2、3、4、7 共 4 个样本
2. 在这 4 个样本中，职业是程序员有 3、4 共 2 个样本，则其概率为：2/4=0.5
3. 在在 2 个样本中，体型超重的有 4 共 1 个样本，则其概率为：1/2 = 0.5
4. 则 P(程序员, 超重|喜欢) = 0.5 * 0.5 = 0.25

简言之：
条件概率：在去掉部分样本的情况下，计算某些样本的出现的概率，表示为：P(B|A)
联合概率：多个事件同时发生的概率是多少，表示为：P(AB) = P(B)*P(A|B)

贝叶斯公式

1. P( C) 表示 C 出现的概率
2. P(W|C) 表示 C 条件 W 出现的概率
3. P(W) 表示 W 出现的概率
   
   -1. P(C|W) = P(喜欢|程序员，超重)
   -2. P(W|C) = P(程序员，超重|喜欢)
   -3. P© = P(喜欢)
   -4. P(W) = P(程序员，超重)

1. 根据训练样本估计先验概率P©：P(喜欢) = 4/7
2. 根据条件概率P(W|C)调整先验概率：P(程序员,超重|喜欢) = 1/4
3. 此时我们的后验概率P(C|W)为：P(程序员,超重|喜欢) * P(喜欢) = 4/7 * 1/4 = 1/7
4. 那么该部分数据占所有既为程序员，又超重的人中的比例是多少呢？
   1. P(程序员,超重) = P(程序员) * P(超重|程序员) = 3/7 * 2/3 = 2/7
   2. P(喜欢|程序员, 超重) = 1/7 ➗ 2/7 = 0.5

朴素贝叶斯

我们发现，在前面的贝叶斯概率计算过程中，需要计算 P(程序员,超重|喜欢) 和 P(程序员, 超重) 等联合概率，为了简化联合概率的计算，朴素贝叶斯在贝叶斯基础上增加：特征条件独立假设，即：特征之间是互为独立的。
此时，联合概率的计算即可简化为：

1. P(程序员,超重|喜欢) = P(程序员|喜欢) * P(超重|喜欢)
2. P(程序员,超重) = P(程序员) * P(超重)

拉普拉斯平滑系数

由于训练样本的不足，导致概率计算时出现 0 的情况。为了解决这个问题，我们引入了拉普拉斯平滑系数。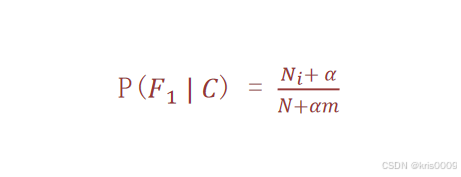

1. α 是拉普拉斯平滑系数，一般指定为 1
2. N_i 是 F1 中符合条件 C 的样本数量
3. N 是在条件 C 下所有样本