数据结构导论之拓扑排序

武梓龙_Wzill

已于 2023-07-28 21:49:45 修改

阅读量638

点赞数

分类专栏：自考文章标签：数据结构算法

于 2021-08-28 09:52:56 首次发布

本文链接：https://blog.csdn.net/weixin_45490198/article/details/119964023

版权

自考专栏收录该内容

4 篇文章

订阅专栏

概念说明

拓扑排序是基于有向无环图的排序算法。有向无环图是一个图，其中的边都是有方向的，并且不存在环路，即没有从一个节点出发经过若干条边后又回到该节点的路径。

算法思想

拓扑排序的基本思想是通过不断删除入度为 0 的节点来确定节点的排序顺序。入度表示指向该节点的边的数量。在拓扑排序过程中，每次选择入度为 0 的节点，并将其从图中删除，同时更新其他节点的入度。重复这个过程直到所有节点都被处理。

操作步骤

问题说明

设G=（V,E）是一个具有n个顶点的有向图，V中顶点的序列v1，v2，……，vn称为一个拓扑序列，且当仅当该顶点序列满足下列条件：在有向图G中，从顶点vi到vj有一条路径，则在拓扑序列中顶点vi必须排在顶点vj之前，找一个有向图的一个拓扑序列的过程称为拓扑序列。

问题分析

1.从图中选择一个入度为0的顶点，输出该顶点。

2.从图中删除该顶点以及相关联的弧，调整被删弧的弧头节点的入度。

3.重复执行1和2步骤直到所有入度为0的顶点都被输出，拓扑排序完成，或者图中没有入度为0的顶点。

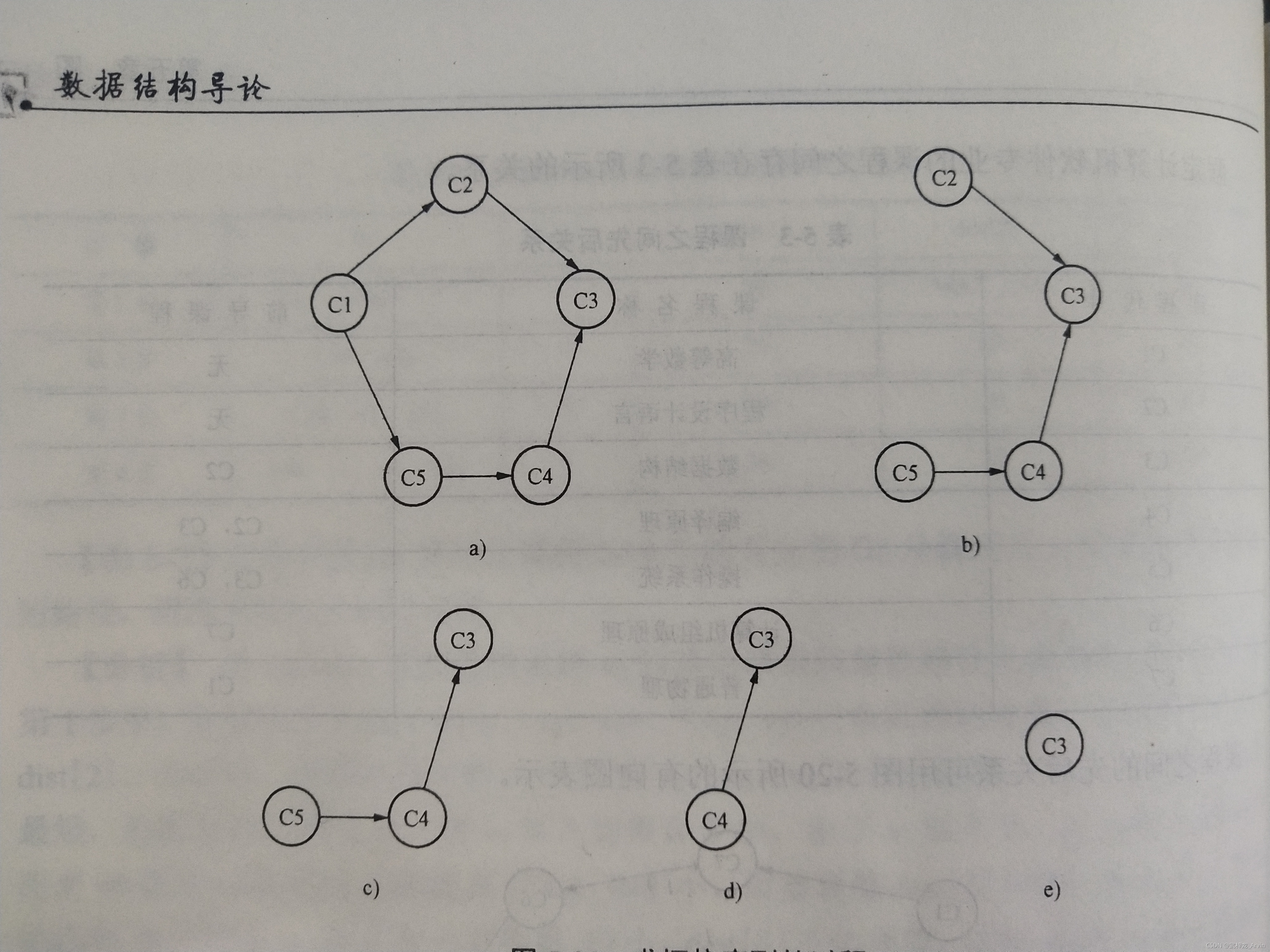
图中的拓扑排序的步骤为：C1，C2，C5，C4，C3

时间复杂度

拓扑排序算法的时间复杂度为 O(V + E)，其中 V 表示节点的数量，E 表示边的数量。

算法步骤

初始化：创建一个队列，用于存储入度为 0 的节点。
计算入度：遍历图中的所有节点，计算每个节点的入度。
入度为 0 的节点入队：将入度为 0 的节点加入队列。
循环处理节点：从队列中取出一个节点，将其输出，并将其所有邻接节点的入度减 1。如果邻接节点的入度变为 0，则将其加入队列。
重复上述步骤直到队列为空。

代码实现

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class TopologicalSort {
    public List<Integer> topologicalSort(int numCourses, int[][] prerequisites) {
        // 构建邻接表
        List<List<Integer>> adjacencyList = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            adjacencyList.add(new ArrayList<>());
        }
        int[] indegree = new int[numCourses];

        for (int[] prerequisite : prerequisites) {
            int course = prerequisite[0];
            int prerequisiteCourse = prerequisite[1];
            adjacencyList.get(prerequisiteCourse).add(course);
            indegree[course]++;
        }

        // 初始化队列，将入度为 0 的节点入队
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0) {
                queue.offer(i);
            }
        }

        List<Integer> result = new ArrayList<>();
        // 循环处理节点
        while (!queue.isEmpty()) {
            int course = queue.poll();
            result.add(course);

            // 将邻接节点的入度减 1，如果入度变为 0，则加入队列
            for (int neighbor : adjacencyList.get(course)) {
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    queue.offer(neighbor);
                }
            }
        }

        // 如果有环，即存在入度不为 0 的节点，则无法完成拓扑排序
        if (result.size() != numCourses) {
            return new ArrayList<>();
        }

        return result;
    }

    public static void main(String[] args) {
        int numCourses = 4;
        int[][] prerequisites = {{1, 0}, {2, 0}, {3, 1}, {3, 2}};
        TopologicalSort topologicalSort = new TopologicalSort();
        List<Integer> result = topologicalSort.topologicalSort(numCourses, prerequisites);
        System.out.println(result); // 输出 [0, 1, 2, 3]
    }
}

我们首先构建了一个邻接表 adjacencyList 来表示有向图的边关系，同时使用数组 indegree 来记录每个节点的入度。然后，我们初始化一个队列 queue，将入度为 0 的节点入队。接着，我们循环处理队列中的节点，将其输出，并将其邻接节点的入度减 1。如果邻接节点的入度变为 0，则将其加入队列。最后，如果结果集中的节点数量与总节点数量不一致，则说明图中存在环，无法完成拓扑排序，返回空列表。否则，返回结果集。