【嵌入式八股15】：控制算法-CSDN博客

本文链接：https://blog.csdn.net/weixin_45498383/article/details/147407660

在嵌入式系统中，控制算法是确保系统精确、稳定运行的核心技术之一。它们用于处理和调整系统状态，保证输出达到预定目标。本文将深入探讨几种常见的控制算法，包括 PID控制、串级PID控制，以及 卡尔曼滤波（KF、EKF、UKF），并详细分析其应用和实现细节。

1. PID 控制算法

PID 控制（Proportional-Integral-Derivative Control）是工业控制系统中最基础、最常用的控制算法之一。PID控制通过计算误差的比例、积分和微分部分来调节系统的输出，使系统能够快速、准确地达到预定目标。

PID 控制的三大核心部分

比例控制（P）：根据当前的误差值进行调节。误差越大，输出值也越大。其计算方式为：

其中，是比例增益，error 为目标值与当前值的差异。
积分控制（I）：对误差进行积分，累计过去的误差，通常用于消除长期的稳态误差。其计算公式为：

是积分增益，积分过程可以使系统保持较小的长期误差。
微分控制（D）：依据误差变化的速率进行调节，用于防止系统过冲和抑制震荡。公式为：

其中，是微分增益，反映误差变化的速度。

PID 控制器的实现

以下是一个典型的 PID 控制器结构的实现代码：

typedef struct {
    uint8_t mode;              // 控制模式
    float Kp, Ki, Kd;         // PID 参数
    float max_out, max_iout;   // 输出限幅
    float set, fdb;            // 目标值与反馈值
    float out, Pout, Iout, Dout;
    float Dbuf[3];             // 微分项
    float error[3];            // 误差项
} PID_t;

float PID_Calc(PID_t *pid, float fdb, float set) {
    if (pid == NULL) {
        return 0.0f;
    }

    // 更新误差历史数据
    pid->error[2] = pid->error[1];
    pid->error[1] = pid->error[0];
    pid->set = set;
    pid->fdb = fdb;
    pid->error[0] = set - fdb;

    // 计算位置环 PID
    if (pid->mode == PID_POSITION) {
        pid->Pout = pid->Kp * pid->error[0];
        pid->Iout += pid->Ki * pid->error[0];
        pid->Dbuf[2] = pid->Dbuf[1];
        pid->Dbuf[1] = pid->Dbuf[0];
        pid->Dbuf[0] = pid->error[0] - pid->error[1];
        pid->Dout = pid->Kd * pid->Dbuf[0];

        // 限制积分输出
        LimitMax(pid->Iout, pid->max_iout);

        pid->out = pid->Pout + pid->Iout + pid->Dout;
        LimitMax(pid->out, pid->max_out);
    }
    // 计算变化量环 PID
    else if (pid->mode == PID_DELTA) {
        pid->Pout = pid->Kp * (pid->error[0] - pid->error[1]);
        pid->Iout = pid->Ki * pid->error[0];
        pid->Dbuf[2] = pid->Dbuf[1];
        pid->Dbuf[1] = pid->Dbuf[0];
        pid->Dbuf[0] = pid->error[0] - 2.0f * pid->error[1] + pid->error[2];
        pid->Dout = pid->Kd * pid->Dbuf[0];

        pid->out += pid->Pout + pid->Iout + pid->Dout;
        LimitMax(pid->out, pid->max_out);
    }

    return pid->out;
}

2. 串级 PID 控制

在复杂的控制系统中，特别是电机控制领域，常常使用 串级 PID 控制，它通过将控制系统分为多个环路（如电流环、速度环、位置环）来提高系统的响应速度和控制精度。通常，电流环由电机控制器实现，而用户仅需要设计速度环和位置环。

串级 PID 的优势

适应不同工况：电机负载的变化会影响控制效果，尤其是当负载发生变化时，传统的单一位置环 PID 难以保持稳定。串级 PID 控制通过内环（速度环）快速响应，减少了外环（位置环）参数对负载变化的敏感性。
稳定性提升：如果仅使用位置环 PID，可能会在接近目标位置时出现震荡现象。引入内环速度 PID 可以使得在稳态时，速度趋近于零，从而避免震荡。
速度限制：在串级 PID 控制中，内环的输出可以进行限幅处理，避免了单独使用位置环 PID 时出现过大的电机速度。

串级 PID 调参方法

通常情况下，串级 PID 的参数调节遵循“从内到外”的顺序：首先调整内环（速度环）的 PID 参数，然后再调整外环（位置环）的 PID 参数。

3. 卡尔曼滤波（KF、EKF、UKF）

卡尔曼滤波（Kalman Filter，简称 KF）是一种用于动态系统状态估计的最优滤波器，广泛应用于含噪声的系统中。根据系统的不同特性，卡尔曼滤波有多个变种，包括扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）。

卡尔曼滤波（KF）

卡尔曼滤波最早是为了解决线性系统中的状态估计问题。它通过预测和更新步骤来实现最优状态估计，且能够有效地过滤掉系统中的高斯噪声。

卡尔曼滤波的基本方程如下：

状态预测：
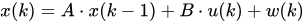
观测更新：

其中，是系统状态，是控制输入，是过程噪声，是观测值，是测量噪声。

扩展卡尔曼滤波（EKF）

EKF 用于处理非线性系统。它通过线性化非线性系统，使用标准的卡尔曼滤波器进行状态估计。虽然 EKF 在处理轻度非线性问题时表现良好，但在非线性较强时，其性能可能会大打折扣。

无迹卡尔曼滤波（UKF）

UKF 是为了解决强非线性系统中的状态估计问题。与 EKF 不同，UKF 采用了一种基于“Sigma 点”的采样方法，避免了对系统进行线性化，从而能够更精确地处理非线性问题。

卡尔曼滤波器实现示例

以下是卡尔曼滤波器的简单实现，用于对输入数据进行噪声过滤：

float Kalman_Filter(float data) {
    static float prevData = 0;
    static float p = 1;  // 估计协方差
    static float q = 1;  // 过程噪声协方差
    static float r = 5;  // 观测噪声协方差
    static float kGain = 0;

    p += q;
    kGain = p / (p + r);  // 计算卡尔曼增益
    data = prevData + (kGain * (data - prevData));  // 计算滤波后的数据
    p =

 (1 - kGain) * p;  // 更新协方差
    prevData = data;
    return data;
}

卡尔曼滤波器结构体实现

typedef struct {
    float LastP;  // 上次估算协方差
    float Now_P;  // 当前估算协方差
    float out;    // 滤波器输出
    float Kg;     // 卡尔曼增益
    float Q;      // 过程噪声协方差
    float R;      // 观测噪声协方差
} KFP;  // 卡尔曼滤波器参数

float kalmanFilter(KFP *kfp, float input) {
    kfp->Now_P = kfp->LastP + kfp->Q;
    kfp->Kg = kfp->Now_P / (kfp->Now_P + kfp->R);
    kfp->out = kfp->out + kfp->Kg * (input - kfp->out);
    kfp->LastP = (1 - kfp->Kg) * kfp->Now_P;
    return kfp->out;
}

总结

控制算法在嵌入式系统中的应用无处不在，特别是在精密控制和数据处理领域。PID控制是最基本也是最常用的控制方法，适用于大多数应用场景。串级PID控制则能够进一步提升复杂系统的精度和响应速度。而卡尔曼滤波（包括KF、EKF和UKF）则为动态系统状态估计和噪声抑制提供了强有力的支持，尤其在高噪声环境下的应用尤为重要。