数据库——关系模型介绍

一、【关系数据结构】

1、关系

1）域(Domain)

定义1–域是一组具有相同数据类型的值的集合。
例如，整数、正整数、实数、大于等于0且小于等于100的正整数、{0,1,2,3,4}等都可以是域。

2）笛卡尔积(Cartesian Product)

定义2–设定一组域D1, D2, …, Dn，在这组域中可以是相同的域。定义D1, D2, …, Dn，的笛卡 尔积为D1×D2×…×Dn={(d1, d2, …, dn) | di∈Di, i=1, 2, …, n}

其中每一个元素(d1, d2, …, dn)叫做一个n元组(n-tuple)或简称元组(Tuple)，元素中的每个 值di(i=1, 2,…, n)叫做一个分量(Component)。 如果Di(i=1, 2,…, n)为有限集，其基数(Cardinal number)为mi (i=1, 2,…, n)，则 D1×D2×…×Dn的基数为：

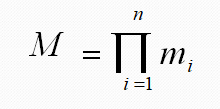
笛卡尔积可以表示为一个二维表，
表中

【例1】 笛卡尔积举例。

给出3个域：
D1=学号集合stno={121001, 121002 }
D2=姓名集合stname={李贤友, 周映雪}
D3=性别集合 stsex={男, 女}
则D1, D2, D3，的笛卡尔积为：
D1×D2×D3={(121001, 李贤友, 男), (121001, 李贤友, 女), (121001, 周映雪, 男), (121001, 周映雪, 女), (121002, 李贤友, 男), (121002, 李贤友, 女), (121002, 周映雪, 男), (121002, 周映雪, 女)} 其中(121001, 李贤友, 男), (121001, 李贤友, 女), (121002, 周映雪, 男)等都是元组， 121001, 121002, 李贤友, 周映雪

男, 女等都是分量，这个笛卡尔积的基数是2×2×2=8，即共有8个元组， 可列成一张二维表，如表1-所示。

↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑表1–D1, D2, D3的笛卡尔积

3）关系(Relation)

定义3–笛卡尔积D1×D2×…×Dn的子集称为D1，D2，…，Dn上的关系，表示为 R(D1，D2，…，Dn) 这里的R 表示关系的名称，n是关系的目或度(Degree)。

• 当n=1时，称该关系为单元关 系或一元关系。
• 当n=2时，称该关系为二元关系。
• 当n=m 时，称该关系为m 元关系。

关系中的每个元素是关系中的元组，通常用t 表示。 在一般情况下，D1，D2，…，Dn的笛卡尔积是没有实际意义的，只有它的某个子集才 有实际意义，举例如下。

【例2】 关系举例

在例1–的笛卡尔积中，许多元组是没有意义的，因为一个学号只标识一个学生的姓名，一个 学生只有一个性别，表1–的一个子集才有意义，才可以表示学生关系，将学生关系取名为S， 表示为S(stno, stname, stsex)，列成二维表如表2–所示。

↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓