培训第一天——快速幂入门

1.从简单的幂运算说起

对于一个接触过一门编程语言的人来说，幂运算是一个最基础的知识了，例如求2的20次方，我们只需要通过如下的代码即可完成

int res = 1;
for (int i=0; i<20; i++)
{
	res *= 2;
}

现在考虑一下这个问题，如果20再大点呢？ 200，20000，甚至2000000……
当然，用循环可以解决，但是花费的时间却是以n的速度线性增长，n很大的时候，花的时间也是相当“可观”。 这里先插一句题外话 ，unsigned long long的最大值也就是2的64次方-1， 也就是说比这个数再大，基础类型就已经存放不下了，如果要求2的200次方，肯定会溢出，所以这里采取一个取模的运算，把最终的结果对1000取模，然后再输出。
模运算
%就是取模的运算符，但如果像上面说的那样，运算完之后再取模，这是很不现实的，当你中间算到某个值的时候，就overflow了，后面算的就都成了错的，为了避免这个问题，我们可以采用一个数学公式（对证明感兴趣的朋友可以百度）

(A*B)%M = (A%M * B%M) % M (%一般是写成mod，懂意思就行)

有了这个公式，我们可以在求幂的每一步都取模，这样就不会有溢出了

接下来我们看一个例子：

	int ans = 1, num=2;
	for (int i=0; i<2000000000; i++)
	{
		ans = ans%1000 * num%1000;//求2的二十亿次方
	}
	printf("%d\n", ans);

运行结果如下：

可以看出来，这花费的是时间还是相当长的，这对大型项目的影响还是很大的，很有必要提升效率！

2.快速幂

那么，为什么会花这么长的时间？肯定是由于循环的次数太多导致的。
有没有什么办法减少循环的次数呢？
二十亿太大了，但我们就得想办法只循环一半次数，这样做的代价就是要将2平方，也就是底数变成了4；
啊！ 我们成功地把循环次数减少了一半，但十亿也还大，我们可以接着把4接着平方，变成16，循环次数又减少了一半……直到经过不断地平方求出了结果！

这就是快速幂核心的思想：二分法

当然，前面说的都是感性上的认识，接着我们用一个简单的例子严谨地考虑一下
比如：求2的10次方，
首先，把指数10折半，也就是要求4的5次方， 到这一步，发现5没办法再折半了，虽然2.5次方在数学上有意义，但是在编程上确是讲不通的。这时怎么办呢？我们可以提出来一个4，变成4*4的四次方，保留左边的4，右边就可以接着折半；那，4的4次方又可以变成16的平方；接着16的平方变成256，别忘了之前提出来的4，结果就是1024.我们总共做了

2 * 2=4，4 * 4=16，16 * 16=256，256*4=1024

四次乘法，更严格的来说是logn次，这里n=10，那上面的2的二十亿次方，也取一下对数，大概是30次吧，这真的是太神奇了，Amazing！

好了，扯了这么多，该看看代码了，根据上面一步步地计算，我们不难发现一个规律，指数为奇数时，那个底数要提出来一个跟最后的结果相乘，然后进行折半偶数的时候直接进行折半。折半的最终结果是指数变成1，
换一种说法，我们需要一个变量来保存最后的结果，在快速幂的过程中，如果指数是偶数，我们就先不用管，让它继续去折半(递归)，反正要的是最后的得数；如果是奇数的话，我们就需要去乘以这个底数（即提出一项），相当于一个保存的功能，因为这些提出的项，最后肯定也还要乘以到结果中的。

根据上面的分析，我们来写一下代码

int quickPow(int x, int n, int mod)//O(logn)
{
	int ans = 1;//初始化
	while (n>0)
	{
		if (1==n%2)
			ans = ans%mod * x%mod;//取模
		n /= 2;
		x = x%mod * x%mod;
	}
	return ans;
}

代码里值得说明的地方：
1.除以是向下取整，无论n的奇偶性，直接除以二就行，这里合并了两种情况；
2.整个过程中不断对n折半，也需要不断对x平方，这点别忘
3.n=1的时候，就是折半结果了，刚好1也是奇数，所以循环条件是n>=1即n>0；

来测试一下这个程序， Amazing！！

3.另一种角度

理解了上面的，快速幂可以说已经学的比较到位了。为了理解更透彻，下面就结合位运算再深入地探讨一下。
分析一下上面的代码，每一轮while循环，x都在不断平方，x的变化过程如下：

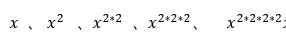
这还看的不够清楚，我们以3的13次方为例，整个变化过程为

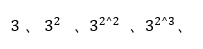
然后模拟运行一下快速幂的程序，会发现最后ans的值为

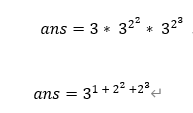
是不是想到了某种东西，别急，把指数补全看看

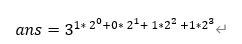
噢（恍然大悟），这不就是13的二进制展开形式吗，就是这么神奇！
这也就是说，我们可以用指数的二进制逐位进行判断，1的话就跟ans相乘，0的话就接着往后走，可以想象成一个选择过滤器，x在不断地平方，每平方一次，都要根据指数二进制上对应的位（0或1）进行选择性相乘，x只管走自己的，判断让指数来决定！
对应到代码上改动比较小，一是把n%2 改成n&1, 二是把n%=2改成n>>=1,即移位运算符，虽然代码差异不大，但理解确实两个角度，直呼过瘾！

int quickPow(int x, int n, int mod)
{
	int ans = 1;//初始化
	while (n>0)
	{
		if (n&1)
			ans = ans%mod * x%mod;//取模
		n>>=1;
		x = x%mod * x%mod;
	}
	return ans;

4.矩阵快速幂

最后谈一下快速幂的拓展应用，幂运算也不是数字独有的，定义了乘法的其他结构也可以，最典型的就是矩阵求幂，当然，根据线代的知识，方阵才能求幂，但这也不妨碍矩阵幂有很多的应用
先来说一下咋实现的：
问题的关键在于定义一个矩阵类型，然后定义它的乘法，取模等运算，到时候只需要把底数换成矩阵就行，没有更多的要求，来看代码：
1.矩阵类的实现

struct Matri{
    int a[15][15];
    int n;
    Matri (int N)
    {
        n = N;
        for (int i=0; i<n; i++)
            for (int j=0; j<n; j++)
                if (i==j)
                    a[i][j] = 1;
                else
                    a[i][j] = 0;
                
    }
    
    Matri operator*(Matri x)
    {
        Matri c(n);
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<n; j++)
                c.a[i][j] = 0;
        }
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<n; j++)
            {
                for (int k=0; k<n; k++)
                {
                    c.a[i][j] += a[i][k] * x.a[k][j];
                }
            }
        }
        return c;
    }
    Matri operator%(int x)
    {
        Matri c(n);
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<n; j++)
            {
                c.a[i][j] = a[i][j]%x;
            }
        }
        return c;
    }
};

用了很多C++语言的特性，构造函数，重载运算符等，这些语言的细节就不再多说了，构造函数是在定义一个单位矩阵。
2.矩阵快速幂

Matri quickPow(Matri x, int n, int m)
{
    
    Matri res(x.n);
    while (n>0)
    {
        if (n&1)
        {
            res = res%m * x%m;
            res  = res%m;
        }
        x = x%m * x%m;
        x = x%m;
        n >>=1;
    }
    return res;
}

值得注意的一点是，在数字的快速幂中，我们的res定义的是1，是乘法的单位元，对于矩阵来说，单位矩阵便是“1”，因此，要通过构造函数建立一个单位矩阵。这点最容易出错。

矩阵快速幂，最典型的应用就是求斐波那契数列，使复杂度降低到了logn，有些求斐波那契数列的题目会卡时间，到时候可以用矩阵快速幂进行优化。

今天的总结就先到这里吧！