B树及插入操作介绍

B树及其相关操作

可能是我理解不到位，B树这个东西嗯。。。可能稍微有点水，总结复习可以参考一下
之前我们已经了解了二叉平衡树中的“AVL树”和“红黑树”，那么接下来看看其他的吧
红黑树及其相关操作
AVL树及其相关操作

B树的诞生

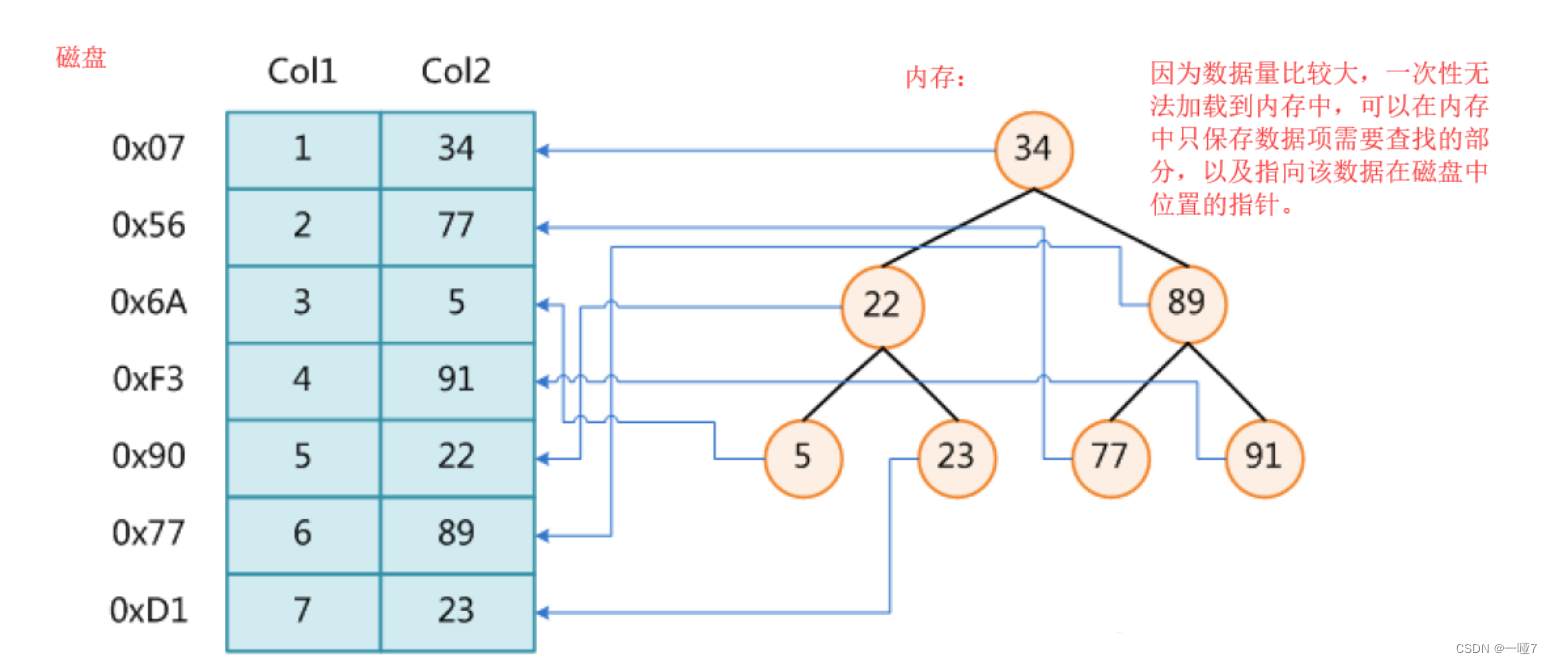
开局一张图，内容慢慢编：

红黑树等数据结构要把数据一次性加载到内存，但是嗯。。。如果数据足够大呐？于是，我们想到用地址链接，只在内存中保存了每一项数据信息中需要查找的字段以及数据在磁盘中的位置，整体的数据实际还在磁盘中如上图所示。但是又带来了两个新的为题：

1. 树的高度比较高，查找时最差情况下要比较树的高度次
2. 数据量如果特别大时，树中的节点可能无法一次性加载到内存中，需要多次IO

聪明的程序员们就像裁缝一样哪里破了补哪里，有问题？对症下药呗，于是提了两个新的解决方案：

1. 提高IO的速度(嗯。。。花钱嘛，买贵的速度快)
2. 降低树的高度（嗯。。。多叉树平衡树诞生了）

B树的一般性质

一棵M阶(M>2)的B树，是一棵平衡的M路平衡搜索树，可以是空树或者满足以下性质：

1. 根节点至少有2个孩子
2. 每个非根节点至少有M/2-1(上取整)个关键字,至多有M-1个关键字，并且以升序排列
   例如：当M=3的时候，至少有3/2=1.5，向上取整等于2，2-1=1个关键字，最多 是2个关键字
3. 每个非根节点至少有M/2(上取整)个孩子,至多有M个孩子
   例如：当M=3的时候，至少有3/2=1.5，向上取整等于2个孩子。最多有3个孩 子。
4. key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间
5. 所有的叶子节点都在同一层

B树的操作理解

首先看一下下面这个图感受一下

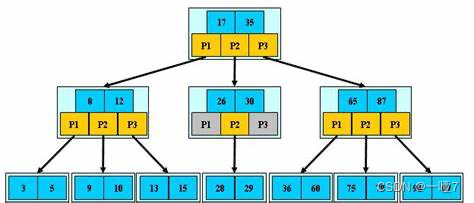
下面我们以插入「53, 139, 75, 49, 145, 36, 101」为例构建B树的过程如下：

好了插入过程的图看完了那我们总结一下就开始正式操作吧：

1. 如果树为空，直接插入新节点中，该节点为树的根节点
2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)
3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
4. 按照插入排序的思想将该元素插入到找到的节点中
5. 检测该节点是否满足B-树的性质：即该节点中的元素个数是否等于M，如果小于则满足
6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：

• 申请新节点
• 找到该节点的中间位置
• 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
• 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续4

7. 如果向上已经分裂到根节点的位置，插入结束

---

B树插入操作

package 树.B树;

import javafx.util.Pair;

public class BTree {
    class BTNode {
        int size;
        int[] key;
        BTNode[] sub;
        BTNode parent;

        BTNode(int m) {
            key = new int[m];
            sub = new BTNode[m + 1];
            size = 0;
        }
    }

    BTNode root;
    int M = 3;

    // 返回值的含义：
// 键值对中的key：表示元素所在的节点
// 键值对中的value：表示元素在该节点中的位置
// 当value为-1时，表示该元素在节点中不存在
    public Pair<BTNode, Integer> find(int key) {
        BTNode cur = root;
        BTNode parent = null;
        while (cur != null) {
            int index = 0;
            while (index < cur.size) {
                if (key == cur.key[index])
                    return new Pair<BTNode, Integer>(cur, index);
                else if (key < cur.key[index]) // 在该节点的第index个孩子中查找
                    break;
                else
                    index++; // 在该节点中继续查找
            }

// 在cur节点的第index的孩子节点中找key
            parent = cur;
            cur = cur.sub[index];
        }
// 未找到key，索引返回-1
        return new Pair<BTNode, Integer>(parent, -1);
    }


    // 采用插入排序的思想插入在cur节点中插入key以及分列出的sub孩子
    void insertKey(BTNode cur, int key, BTNode sub) {
        int end = cur.size - 1;
        while (end >= 0 && key < cur.key[end]) {
// 将该位置元素以及其右侧孩子往右搬移一个位置

            cur.key[end + 1] = cur.key[end];
            cur.sub[end + 2] = cur.sub[end + 1];
            end--;
        }
// 插入元素和孩子节点，更size
        cur.key[end + 1] = key;
        cur.sub[end + 2] = sub;
        cur.size++;
        if (sub != null) sub.parent = cur;
    }


    boolean insert(int key) {
        if (null == root) {
            root = new BTNode(M);
            root.key[0] = key;
            root.size = 1;
            return true;
        }

// 查找当前元素的插入位置
// 如果返回的键值对的value不等于-1，说明该元素已经存在，则不插入
        Pair<BTNode, Integer> ret = find(key);
        if (-1 != ret.getValue()) {
            return false;
        }
// 注意：在B-Tree中找到的待插入的节点都是叶子节点
        BTNode cur = ret.getKey();
        int k = key;
        BTNode sub = null; // 主要在分列节点时起作用
        while (true) {
            insertKey(cur, k, sub);

// 元素插入后，当前节点可以放的下，不需要分列
            if (cur.size < M) break;

// 新节点插入后，cur节点不满足B-Tree的性质，需要对节点进行分列
// 具体分列的方式
// 1. 找到节点的中间位置
// 2. 将中间位置右侧的元素以及孩子插入到分列的新节点中
// 3. 将中间位置的元素以及分列出的新节点向当前分列节点的双亲中继续插入
            int mid = (cur.size >> 1);

            BTNode newNode = new BTNode(M);
// 将中间位置右侧的所有元素以及孩子搬移到新节点中
            int i = 0;
            int index = mid + 1; // 中间位置的右侧
            for (; index < cur.size; ++index) {
// 搬移元素
                newNode.key[i] = cur.key[index];

// 搬移元素对应的孩子
                newNode.sub[i++] = cur.sub[index];

// 孩子被搬移走了，需要重新更新孩子双亲
                if (cur.sub[index] != null) cur.sub[index].parent = newNode;
            }

// 注意：孩子要比双亲多搬移一个newNode.subs[i] = cur.subs[index]; if(cur.subs[index] != null)
            cur.sub[index].parent = newNode;

// 更新newNode以及cur节点中剩余元素的个数
// cur中的i个元素搬移到了newNode中
// cur节点的中间位置元素还要继续向其双亲中插入newNode.size = i;
            cur.size = cur.size - i - 1;

            k = cur.key[mid];

// 说明分列的cur节点刚好是根节点
            if (cur == root) {
                root = new BTNode(M);

                root.key[0] = k;


                root.sub[0] = cur;
                root.sub[1] = newNode;
                root.size = 1;
                cur.parent = root;
                newNode.parent = root;
                break;
            } else {
// 继续向双亲中插入
            sub = newNode; cur = cur.parent;
            }
        }

        return true;
    }
}

---

本来是打算B树一次讲完的，这个还是鸽一下吧，后续会重新补详细过程
下面先来看一下B树的两个变种

B+树

B+树的特性：

1. 所有关键字都出现在叶子节点的链表中(稠密索引)，且链表中的节点都是有序的。
2. 不可能在非叶子节点中命中。
3. 非叶子节点相当于是叶子节点的索引(稀疏索引)，叶子节点相当于是存储数据的数据层。
4. 更适合文件索引系统

B*树

给B+树的非根和非叶子节点再增加指向兄弟节点的指针。

简单总结