2018ACM四川省赛G.Grisaia（超棒的杜教筛好题）

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

---

G. Grisaia（灰色的果实好耶《灰色的果实(The Fruit of Grisaia)》）

Weblink

https://www.oj.swust.edu.cn/problem/show/2810

Problem

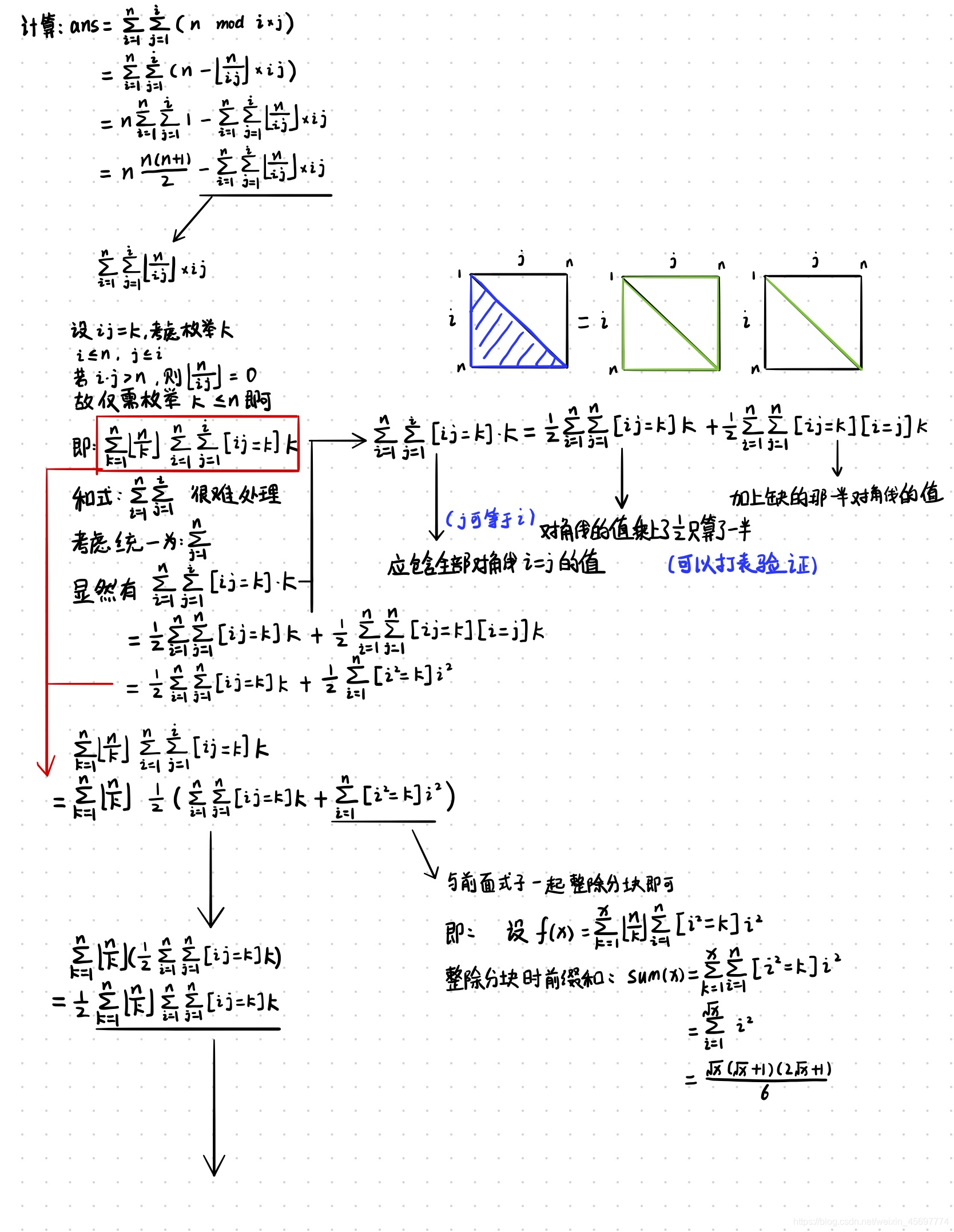
计算：

$$ans=\sum _{i=1}^n\sum _{j=1}^i(nmod(i\times j))$$

其中 $T\le 5,n\le 10^{11}$

Solution

使用模的展开式将上述和式展开后，显然套路枚举 $k=i\times j$，由于 $n\le 10^{11}$，杜教筛即可。

筛出：

$$\begin{gathered} f(x)=x\times d(x) \\ g(x)=x\times \mu (x) \end{gathered}$$

然后整除分块即可。

Hint

注意 $n\le 10^{11}$，中间多处会爆 long long，强转成 __int128 即可。

（因为这个wa了8发hhh，五颜六色的）

Code

#include <bits/stdc++.h>
   
using namespace std;
#define int long long
#define ll __int128