逆向设计相关算法学习（一）——梯度下降（Gradient Descent）

以下主要翻译这一篇：Gradient Descent: All You Need to Know

梯度下降是机器学习中最常用的学习算法，这篇文章将向您展示您需要了解的几乎所有内容。

几乎所有机器学习模型中都使用的一种算法是什么？ 这是梯度下降。 该算法有一些变体，但这本质上是任何 ML 模型的学习方式。 没有这个，机器学习就不会是现在的样子。

在这篇文章中，我将用一点数学来解释梯度下降。 老实说，GD（梯度下降）本身并不涉及很多数学（我稍后会解释）。 我将用类比来替换底层数学的大部分复杂性，有些是我自己的，有些来自互联网。

以下是我将要讨论的内容：

$\bullet$GD的观点：解释整个算法是什么。
$\bullet$不同类型的 GD 算法：了解 GD 的不同变化。
$\bullet$代码实现：用 Python 编写代码来演示 GD。

1.GD的观点

梯度下降需要一个成本函数，cost function（成本函数有很多种）。 我们需要这个成本函数，因为我们想最小化它。 最小化任何函数意味着找到该函数中最深的山谷。 请记住，成本函数用于监控 ML 模型的预测误差。 因此，最小化这一点，基本上意味着尽可能降低误差值或提高模型的准确性。 简而言之，我们通过在调整模型的参数（权重weights和偏差weights）的同时迭代训练数据集来提高准确性。

因此，GD 的重点是最小化成本函数。

该算法的核心是获得最低误差值的过程。类似地，这可以看作是走进一个山谷，试图找到金子（最低误差值）。当我们在这里的时候，我相信你想知道如果你只能看到你周围的山谷，我们如何在一个有很多山谷的函数中找到最深的山谷？我不会讨论解决这个问题的方法，因为这超出了这篇文章的范围（适用于初学者）。但是，只要知道有办法解决这个问题。

展望未来，为了找到成本函数（相对于一个权重）中的最低误差（最深谷），我们需要调整模型的参数。我们对它们进行了多少调整？输入微积分。使用微积分，我们知道函数的斜率是函数对值的导数。这个斜坡总是指向最近的山谷！

在这里（在图片中），我们可以看到成本函数（名为“Error”，符号“J”）与一个权重的关系图。现在，如果我们计算成本函数相对于这个权重的斜率（我们称之为 dJ/dw），我们会得到我们需要移动的方向，以达到局部最小值（最近的最深谷）。现在，让我们想象一下我们的模型只有一个权重。

成本函数“J”针对一个权重绘制。

注意：当我们遍历所有训练数据时，我们会不断为每个权重添加 dJ/dw。 由于成本会根据训练示例不断变化，因此 dJ/dw 也会不断变化。 然后我们将累积值除以训练示例的数量以获得平均值。 然后我们使用（每个权重的）平均值来调整每个权重。

另请注意：本质上，成本函数仅用于监控每个训练示例的误差，而成本函数相对于一个权重的导数是我们需要移动该权重以最小化该训练示例的误差的地方 . 您甚至可以在不使用成本函数的情况下创建模型。 但是您必须使用每个权重的导数 (dJ/dw)。

现在我们已经找到了微调权重的方向，我们需要找到微调权重的幅度。在这里，我们使用学习率（Learning Rate.）。学习率称为超参数（Learning Rate.）。超参数是您的模型所需的值，我们对此知之甚少。这些值主要可以通过反复试验来学习。超参数没有万能的。这个学习率可以被认为是“朝着正确方向迈出的一步”，其中方向来自 dJ/dw。

这是仅针对一个权重绘制的成本函数。在真实模型中，我们对所有权重执行上述所有操作，同时迭代所有训练示例。即使在相对较小的 ML 模型中，您也将拥有不止 1 或 2 个权重。这让事情变得更难可视化，因为现在，您的图表将具有我们大脑甚至无法想象的维度。

回到我之前说的那一点，“老实说，GD（梯度下降）本质上并不涉及很多数学（我稍后会解释）。”嗯，是时候了。

1.1 更多关于梯度

对于成本函数，GD 还需要一个 dJ/dw 的梯度（成本函数相对于单个权重的导数，对所有权重进行）。 这个 dJ/dw 取决于您选择的成本函数。 成本函数有很多种， 最常见的是均方误差成本函数。

这个关于任何权重的导数是（这个公式显示了线性回归的梯度计算）：

这就是GD中的所有数学。看这个，你可以看出，GD本质上并不涉及很多数学。它涉及的唯一数学是我们将要进行的乘法和除法。这意味着，您选择的成本函数将影响您对每个权重梯度的计算。

1.2.学习率

我们上面谈到的一切，都是教科书。你可以打开任何关于 GD 的书，它会解释类似于我上面写的内容。甚至每个成本函数的梯度公式都可以在网上找到，而不知道如何自己推导出来。

然而，大多数模型的问题在于学习率。让我们看一下每个权重的更新表达式（j 的范围从 0 到权重的数量，Theta-j 是权重向量中的第 j 个权重，k 的范围从 0 到偏差量，其中 Bk 是偏差向量中的第 k 个偏置）。这里，alpha 是学习率。由此，我们可以看出，我们正在计算 dJ/dTheta-j（权重 Theta-j 的梯度），然后我们在该方向上迈出了一个大小为 alpha 的步长。因此，我们正在向下移动梯度。要更新偏差，请将 Theta-j 替换为 B-k。

如果这个步长 alpha 太大，我们会超过最小值，也就是说，我们甚至无法到达最小值。 如果 alpha 太小，我们将需要太多的迭代才能达到最小值。 所以，alpha需要恰到好处。 这让很多人感到困惑，老实说，它也让我困惑了一段时间。

1.3. 概括

嗯，就是这样。 这就是GD的全部。 让我们用伪代码总结一下：

注意：这里的权重是向量。在较大的模型中，它们可能是矩阵。这个例子只有一个偏差，但在更大的模型中，这些可能是向量。

$\bullet$对于 i = 0 到训练示例的数量：

1.计算第 i 个训练示例的成本函数相对于每个权重和偏差的梯度。现在你有一个包含每个权重梯度的向量和一个包含偏差梯度的变量。
2.将计算出的权重梯度添加到一个单独的累加器向量中，在您完成对每个训练示例的迭代之后，该向量应该包含多次迭代中每个权重的梯度总和。
3.像权重一样，将偏差的梯度添加到累加器变量中。

$\bullet$现在，在遍历所有训练示例之后执行以下操作：

1.将权重和偏差的累加器变量除以训练示例的数量。这将为我们提供所有权重的平均梯度和偏差的平均梯度。我们将这些称为更新的累加器（UAs）
2.然后，使用下面显示的公式，更新所有权重和偏差。代替 dJ/dTheta-j，您将使用 UA（更新的累加器）作为权重，使用 UA 作为偏差。对偏差做同样的事情。

这只是一次 GD 迭代。

从头到尾重复这个过程进行一些迭代。 这意味着对于 GD 的 1 次迭代，您迭代所有训练示例，计算梯度，然后更新权重和偏差。 然后，您对一些 GD 迭代执行此操作。

2. 不同类型的GD

GD有3种变体：

1.Mini — Batch — GD：这里不是迭代所有训练样例和每次迭代只对单个训练样例进行计算，而是一次处理 n 个训练样例。 对于非常大的数据集，这是一个不错的选择。

2.Stochastic — GD：在这里，我们使用 JUST USE ONE，而不是使用和循环每个训练示例。 对此有几点需要注意：

$\cdot$在每次 GD 迭代中，您需要对训练集进行洗牌并从中选择一个随机训练示例。
$\cdot$由于您只使用了一个训练示例，因此您通往局部最小值的路径会像喝了太多酒后的醉汉一样嘈杂。

3.Batch — GD：这就是我们刚刚在上面讨论的内容。 循环遍历每个训练示例，即 vanilla(basic) GD。

这是一张将 3 与局部最小值进行比较的图片：

3.代码实现

本质上，使用 Batch GD，这就是您的训练代码块的样子（在 Python 中）。

def train(X, y, W, B, alpha, max_iters):
    '''
    Performs GD on all training examples,

    X: Training data set,训练数据集
    y: Labels for training data,训练数据的标签
    W: Weights vector,权重向量
    B: Bias variable,偏差向量
    alpha: The learning rate,学习率
    max_iters: Maximum GD iterations.最大梯度下降迭代次数
    '''
    dW = 0 # Weights gradient accumulator权重梯度累加器
    dB = 0 # Bias gradient accumulator偏差梯度累加器
    m = X.shape[0] # No. of training examples训练样本的个数


    for i in range(max_iters):
        dW = 0 # Reseting the accumulators重置累加器
        dB = 0
        for j in range(m):
            # 1. Iterate over all examples,迭代每个样本
            # 2. Compute gradients of the weights and biases in w_grad and b_grad,计算权重和偏差的梯度
            # 3. Update dW by adding w_grad and dB by adding b_grad,更新梯度
         W = W - alpha * (dW / m) # Update the weights
         B = B - alpha * (dB / m) # Update the bias
    
    return W, B # Return the updated weights and bias.返回已更新的权重和偏差

如果这看起来仍然有点令人困惑，这是我制作的一个小神经网络，它学习预测对 2 个输入执行 XOR 的结果。

以下主要翻译这一篇：

Intro to optimization in deep learning: Gradient Descent
深度学习优化简介：梯度下降

梯度下降的深入解释，以及如何避免局部最小值和鞍点的问题。

在很大程度上，深度学习实际上是解决大量令人讨厌的优化问题。 神经网络只是一个非常复杂的函数，由数百万个参数组成，代表问题的数学解决方案。 考虑图像分类的任务。 AlexNet 是一个数学函数，它接受一个表示图像 RGB 值的数组，并将输出生成为一堆类分数。

通过训练神经网络，我们基本上意味着我们正在最小化损失函数。 这个损失函数的值让我们可以衡量我们的网络在给定数据集上的性能有多远。

一、损失函数

为简单起见，让我们假设我们的网络只有两个参数。 在实践中，这个数字大约是 10 亿，但我们仍然会在整个帖子中坚持使用两个参数示例，以免在尝试可视化事物时让自己发疯。 现在，一个非常好的损失函数的计数可能看起来像这样。

损失函数的轮廓

为什么我说一个非常好的损失函数？因为具有上述轮廓的损失函数就像圣诞老人一样，所以它不存在。然而，它仍然是一个不错的教学工具，可以全面了解梯度下降的一些最重要的想法。所以，让我们开始吧！

x 和 y 轴代表两个权重的值。 z 轴表示两个权重的特定值的损失函数值。我们的目标是找到损失最小的特定权重值。这样的点称为损失函数的最小值（minima）。

一开始你随机初始化了权重，所以你的神经网络可能表现得像喝醉了的自己，将猫的图像分类为人类。这种情况对应于轮廓上的点 A，该点网络表现不佳，因此损失很高。

我们需要找到一种方法以某种方式导航到“谷”的底部到 B 点，那里的损失函数有一个最小值？那么我们该怎么做呢？

梯度下降

二、梯度下降

当我们初始化权重时，我们处于损失图景中的 A 点。我们要做的第一件事是检查，在 x-y 平面上所有可能的方向中，沿着哪个方向移动会导致损失函数值的下降幅度最大。这是我们必须移动的方向。这个方向由与梯度方向完全相反的方向给出。梯度是导数的高维表亲，为我们提供了上升最快的方向。

要绕开它，请考虑下图。在曲线的任何一点，我们都可以定义一个与该点相切的平面。在更高维度，我们总是可以定义一个超平面，但现在让我们坚持 3-D。然后，我们可以在这个平面上有无限的方向。其中，恰好一个方向将为我们提供函数具有最陡峭上升的方向。这个方向由梯度给出。与它相反的方向是最陡下降的方向。这就是算法得名的方式。我们沿着梯度的方向进行下降，因此，它被称为梯度下降。

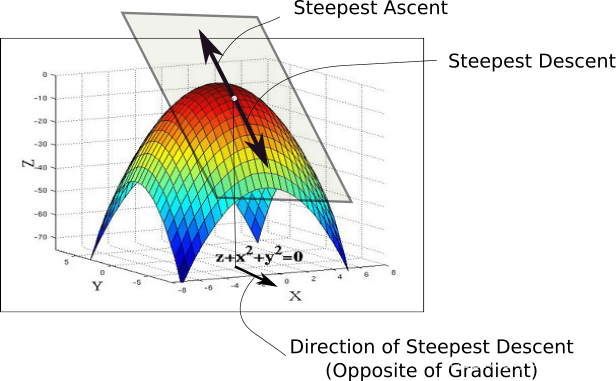
现在，一旦我们有了想要前进的方向，我们就必须决定我们必须采取的步骤的大小。这一步的大小称为学习率（learning rate）。我们必须仔细选择它，以确保我们能够达到最小值。

如果我们走得太快，我们可能会超过最小值，并继续沿着“山谷”的山脊弹跳，而永远不会达到最低标准。走得太慢，训练可能会变得太长而根本不可行。即使不是这样，非常慢的学习率也会使算法更容易陷入最小值，我们将在本文后面介绍。

一旦我们有了梯度和学习率，我们就迈出一步，在我们最终到达的任何位置重新计算梯度，然后重复这个过程。

虽然梯度的方向告诉我们哪个方向的上升最陡峭，但它的幅度告诉我们最陡峭的上升/下降有多陡。因此，在轮廓几乎平坦的最小值处，您会期望梯度几乎为零。事实上，最小值正好为零。

梯度下降动态图

使用过大的学习率

在实践中，我们可能永远不会准确地达到最小值，但我们会一直在靠近最小值的平坦区域中振荡。 当我们在这个区域振荡时，损失几乎是我们可以达到的最小值，并且没有太大变化，因为我们只是在实际最小值附近不断反弹。 通常，当损失值没有以预先确定的次数（例如 10 或 20 次迭代）改善时，我们会停止迭代。 当这种情况发生时，我们说我们的训练已经收敛，或者说已经收敛。

三、一个常见的错误

让我暂时离题。 如果你在谷歌上搜索梯度下降的可视化，你可能会看到一条从一点开始到最小值的轨迹，就像上面展示的动画一样。 然而，这给你一个关于梯度下降真正是什么的非常不准确的画面。 我们采用的轨迹完全局限于 x-y 平面，该平面包含权重。

如上面的动画所示，梯度下降根本不涉及沿 z 方向移动。 这是因为只有权重是自由参数，由 x 和 y 方向描述。 我们采用的实际轨迹在 x-y 平面中定义如下。

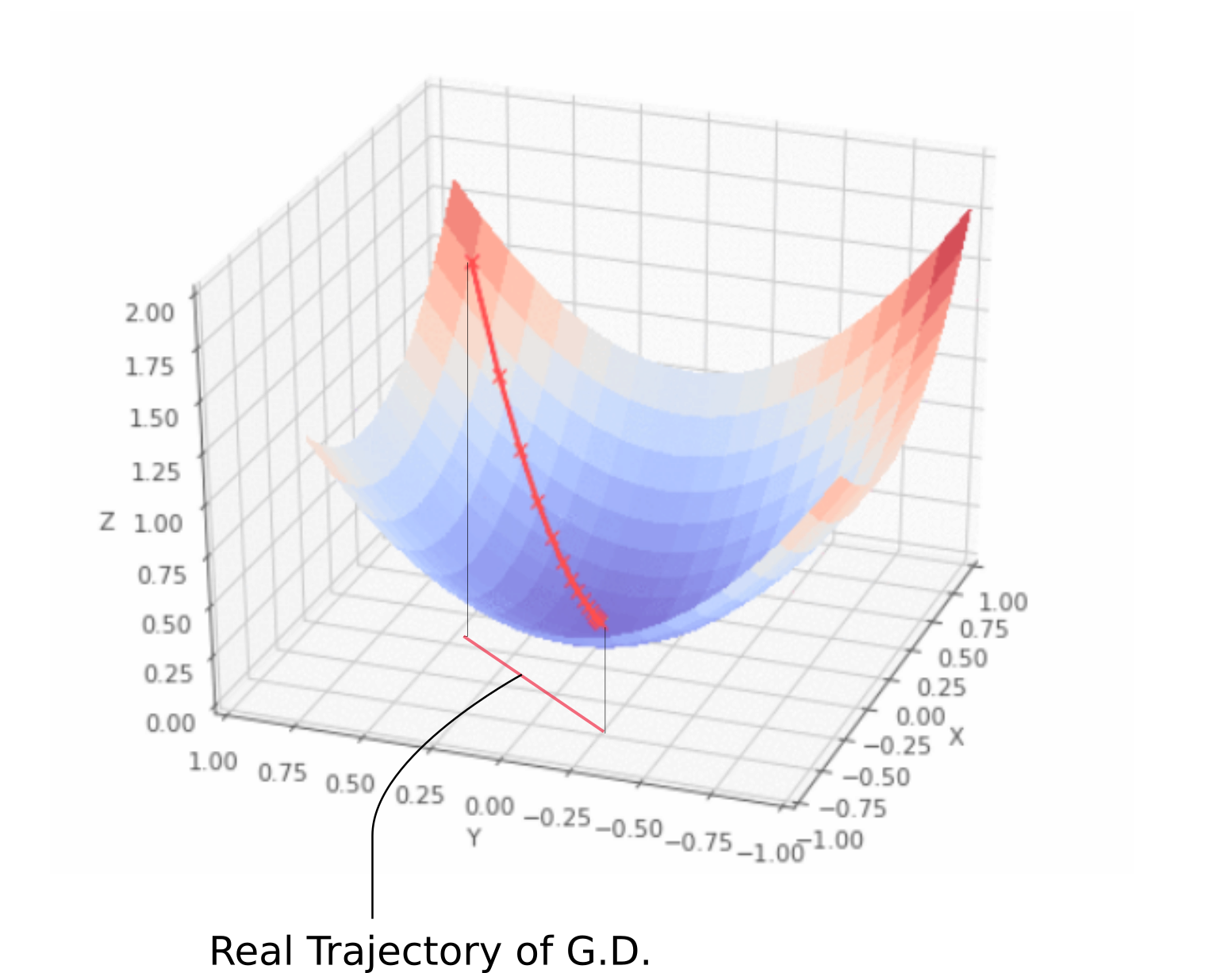
真实梯度下降轨迹

x-y 平面中的每个点都代表一个独特的权重组合，我们想要一组由最小值描述的权重。

四、基本方程

描述梯度下降更新规则的基本方程是

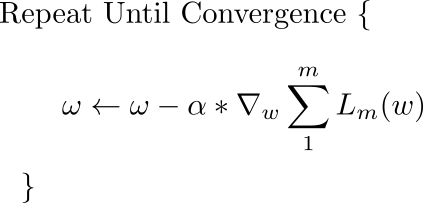
此更新在每次迭代期间执行。 这里，w 是权重向量，位于 x-y 平面上。 从这个向量中，我们减去损失函数相对于权重乘以 alpha （即学习率）的梯度。 梯度是一个向量，它为我们提供了损失函数上升最快的方向。 最快速下降的方向是与梯度完全相反的方向，这就是我们从权重向量中减去梯度向量的原因。

如果想象向量对您来说有点困难，那么几乎相同的更新规则会同时应用于网络的每个权重。 唯一的变化是，由于我们现在对每个权重单独执行更新，所以上面等式中的梯度被替换为梯度向量沿特定权重表示的方向的投影。

对所有权重同时进行此更新。

在减去之前，我们将梯度向量乘以学习率。这代表了我们之前谈到的步骤。意识到即使我们保持学习率不变，步长的大小也会随着梯度大小的变化而变化，而不是损失轮廓的陡度。当我们接近最小值时，梯度接近零，我们朝着最小值迈出越来越小的步幅。

从理论上讲，这很好，因为我们希望算法在接近最小值时采取更小的步骤。步长太大可能会导致它超出最小值并在最小值的脊之间反弹。

梯度下降中广泛使用的技术是具有可变的学习率，而不是固定的学习率。最初，我们可以承受很大的学习率。但稍后，当我们接近最小值时，我们希望放慢速度。实现此策略的一种方法称为**模拟退火（Simulated annealing）**或衰减学习率。在这种情况下，学习率每固定迭代次数衰减一次。

五、梯度下降的挑战 #1：局部最小值

好吧，到目前为止，梯度下降的故事似乎是一个非常快乐的故事。 好吧。 让我为你破坏它。 还记得我说过我们的损失函数非常好，而这样的损失函数并不存在吗？ 他们没有。

首先，神经网络是复杂的函数，我们的假设函数中有很多非线性变换。 由此产生的损失函数看起来不是一个漂亮的碗，我们只能收敛到一个最小值。 事实上，这种漂亮的圣诞老人损失函数被称为凸函数（ convex functions）（总是向上弯曲的函数），而深度网络的损失函数几乎不是凸函数。 事实上，它们可能看起来像这样。

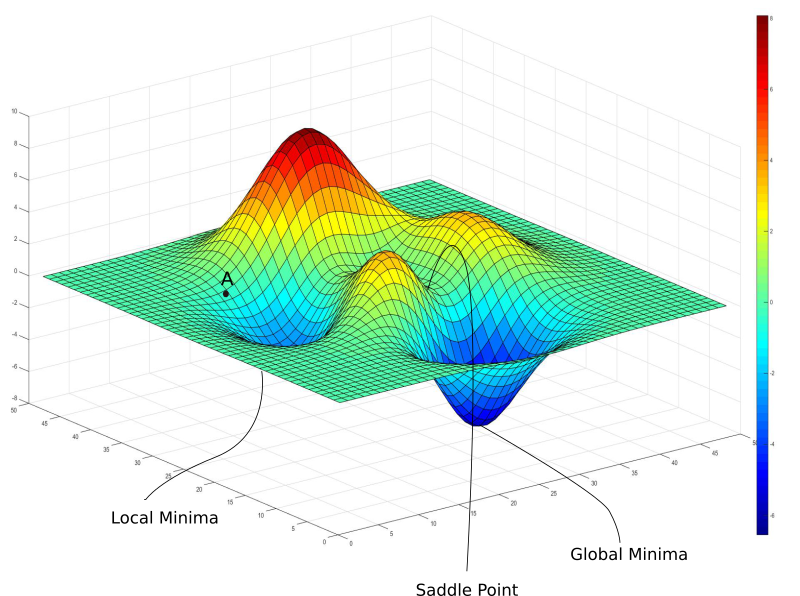
在上图中，存在梯度为零的局部最小值。但是，我们知道它们并不是我们能达到的最低损失，即对应于全局最小值的点。现在，如果你在 A 点初始化你的权重，那么你将收敛到局部最小值，一旦你收敛到局部最小值，梯度下降就不可能让你离开那里。

梯度下降是由梯度驱动的，在任何最小值的底部都将为零。之所以调用局部最小值，是因为损失函数的值在局部区域中的该点处是最小值。然而，由于损失函数的值在那里最小，全局最小值被称为全局最小值，在整个域中全局损失函数。

更糟糕的是，考虑到像我们正在考虑的 3-d 轮廓在实践中从未真正发生过的事实，损失轮廓甚至可能更复杂。在实践中，我们的神经网络可能有大约 10 亿个权重，给我们一个大约 (10 亿 + 1) 个维度的函数。我什至不知道该图中零的数量。

事实上，甚至很难想象如此高维的函数是什么。然而，鉴于这些天在深度学习领域的天赋，人们已经想出了在 3-D 中可视化损失函数轮廓的方法。最近的一篇论文开创了一种称为**过滤器标准化（ Filter Normalization）**的技术，解释了这超出了本文的范围。然而，它确实让我们了解了我们处理的损失函数的潜在复杂性。例如，以下轮廓是 CIFAR-10 数据集上 VGG-56 深度网络损失函数的损失轮廓的构造 3-D 表示。

复杂的损失景观图片来源：https://www.cs.umd.edu/~tomg/projects/landscapes/

正如你所看到的，损失景观图片是局部最小值。

六、梯度下降的挑战 #2：鞍点

我们学到的关于梯度下降限制的基本教训是，一旦它到达梯度为零的区域，无论最小值的质量如何，它几乎不可能逃脱它。 我们面临的另一种问题是鞍点（景观图片）问题，看起来像这样。

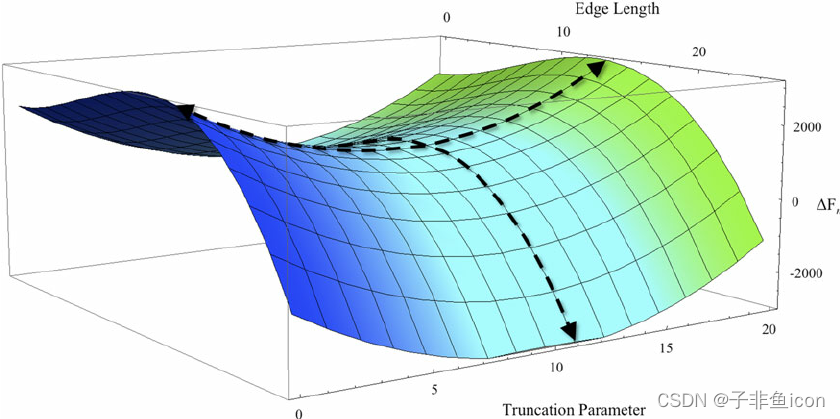
鞍点

您还可以在前面的图片中看到两个“山”相遇的鞍点。

鞍点得名于与其相似的马鞍。 虽然它是一个方向 (x) 上的最小值，但它是另一个方向上的局部最大值，如果轮廓朝向 x 方向更平坦，GD 将继续在 y 方向上来回振荡，并给我们一种错觉，即我们 已经收敛到一个最小值。

七、随机应变

那么，我们如何避开局部最小值和鞍点，同时尝试收敛到全局最小值。 答案是随机性。

到目前为止，我们正在使用通过对训练集的所有可能示例的损失求和而创建的损失函数进行梯度下降。 如果我们进入局部最小值或鞍点，我们就会陷入困境。 帮助 GD 摆脱这些问题的一种方法是使用所谓的随机梯度下降。

在随机梯度下降中，我们不是通过计算通过对所有损失函数求和创建的损失函数的梯度来采取步骤，而是通过仅计算一个随机采样（无替换）示例的损失梯度来采取步骤。 与随机选择每个示例的随机梯度下降相比，我们早期的方法在一个批次中处理所有示例，因此被称为批量梯度下降。

更新规则相应修改。

随机梯度下降的更新规则

这意味着，在每一步，我们都在获取损失函数的梯度，这与我们的实际损失函数（这是每个示例损失的总和）不同。这个“one-example-loss”在某个特定点的梯度实际上可能指向与“all-example-loss”梯度略有不同的方向。

这也意味着，虽然“all-example-loss”的梯度可能会将我们推到局部最小值，或者让我们陷入鞍点，但“one-example-loss”的梯度可能指向不同的方向，并可能帮助我们避开这些。

人们还可以考虑一个点，它是“所有示例损失”的局部最小值。如果我们在做批量梯度下降，我们会卡在这里，因为梯度总是指向局部最小值。然而，如果我们使用随机梯度下降，这个点可能不在“one-example-loss”的损失轮廓中的局部最小值附近，允许我们远离它。

即使我们陷入“单例损失”的最小值，下一个随机采样数据点的“单例损失”的损失情况可能会有所不同，从而使我们能够继续前进。

当它确实收敛时，它会收敛到几乎所有“单例损失”的最小值。经验也表明，鞍点非常不稳定，轻轻一推就足以逃脱。

那么，这是否意味着在实践中，应该总是执行这个单例随机梯度下降？

八、批量大小

答案是不。尽管从理论的角度来看，随机梯度下降可能会给我们最好的结果，但从计算的角度来看，它并不是一个非常可行的选择。当我们使用通过对所有单个损失求和创建的损失函数执行梯度下降时，可以并行计算单个损失的梯度，而在随机梯度下降的情况下必须逐步计算。

因此，我们所做的是一种平衡行为。我们不使用整个数据集或仅使用单个示例来构建我们的损失函数，而是使用固定数量的示例，例如 16、32 或 128 来形成所谓的小批量（mini-batch）。该词用于与一次处理所有示例形成对比，通常称为批量梯度下降（Batch Gradient Descent）。选择小批量的大小是为了确保我们获得足够的随机性来避免局部最小值，同时利用并行处理的足够计算能力。

九、重新审视局部最小值：它们并没有你想象的那么糟糕

在对抗局部最小值之前，最近的研究表明局部最小值并不一定很糟糕。在神经网络的损失情况下，最小值太多了，“好的”局部最小值可能与全局最小值一样好。

为什么我说“好”？因为您仍然可能陷入由于训练示例不稳定而创建的“坏”局部最小值。考虑到神经网络的高维损失函数，“好的”局部最小值，或者在文献中经常被称为最优局部最小值，可以大量存在。

还可能注意到许多神经网络执行分类。如果局部最小值对应于它为正确标签产生 0.7-0.8 之间的分数，而全局最小值对应于它为相同示例的正确标签产生 0.95-0.98 之间的分数，则输出类预测对于两者都是相同的。

**最小值的理想属性应该是它应该位于更平坦的一侧。**为什么？因为平坦的最小值很容易收敛到，所以越过最小值的机会更少，并且在最小值的脊之间弹跳。

更重要的是，我们期望测试集的损失表面与我们进行训练的训练集的损失表面略有不同。对于平坦且宽的最小值，损失不会因为这种变化而发生太大变化，但对于窄最小值则不是这样。我们试图提出的观点是更平坦的最小值可以更好地概括，因此是可取的。

十、重新审视学习率

最近，关于学习率调度的研究激增，以解释损失情况下的次优最小值。即使学习率下降，人们也可能陷入局部最小值。传统上，训练要么进行固定次数的迭代，要么可以在损失没有改善后的 10 次迭代后停止。这在书面上被称为早期停止（early stopping）。

拥有快速的学习率也有助于我们在训练的早期越过局部最小值。

人们还将提前停止与学习率衰减结合起来，每次在 10 次迭代后损失没有改善时，学习率就会衰减，最终在速率低于某个确定的阈值后停止。

近年来，循环学习率很流行，学习率是慢慢增加，然后减少，并以循环方式继续。

Leslie N. Smith 提出的用于循环学习率的“Triangular”和“Triangular2”方法。 在左边的情节 min 和 max lr 保持不变。 在右侧，每个循环后差值减半。 图片来源：Hafidz Zulkifli

带有热重启（warm restarts）的随机梯度下降基本上将学习率退火到下限，然后将学习率恢复到其原始值。
（退火就是下降，余弦退火就是学习率类似余弦函数慢慢下降。热重启就是在学习的过程中，学习率慢慢下降然后突然回弹，然后继续慢慢下降）

对于学习率如何下降，我们也有不同的时间表，从指数衰减到余弦衰减

余弦退火结合重启

最近的一篇论文介绍了一种称为随机权重平均（tochastic Weight Averaging）的技术。 作者开发了一种方法，他们首先收敛到最小值，缓存权重，然后将学习率恢复到更高的值。 然后，这种更高的学习率将算法从最小值推动到损失表面中的随机点。 然后使算法再次收敛到另一个最小值。 重复几次。 最后，他们对所有缓存权重集所做的预测进行平均，以产生最终预测。

一种称为随机权重平均的技术

十一、结论

所以，这是关于梯度下降的介绍性文章，自从关于反向传播的开创性论文表明你可以通过计算梯度来训练神经网络以来，它一直是深度学习优化的工作之马。 然而，关于梯度下降还有一个我们没有在这篇文章中讨论过的缺失块，那就是解决病态曲率问题。 普通随机梯度下降的扩展，如 Momentum、RMSProp 和 Adam 用于克服这个重要问题。