堆(一)——删除堆顶元素、插入元素、堆排序_堆排序删除堆顶元素怎么排-CSDN博客

本文链接：https://blog.csdn.net/weixin_45728685/article/details/105115912

堆的结构特点

堆排序是一个可以高效实现排序的算法，复杂度是O(nlogn)和之前的快速排序与归并排序的复杂度相同，而它高效的排序依赖于它的结构特点

堆是一个完全二叉树
堆中每一个节点的值都必须大于等于(或者小于等于)其子树中每个结点的值

第二点是说明每个节点都必须大于等于(或者小于等于)其左右子结点的值。

其中大于等于其左右节点的堆叫大顶堆，小于等于其左右节点的堆叫小顶堆

堆的存储结构分析

由于堆是一个完全二叉树，所以它可以用非常简便的数组来进行存储。

数组存储的元素就是节点的值，而数组下标位置就代表着该结点在堆中的位置

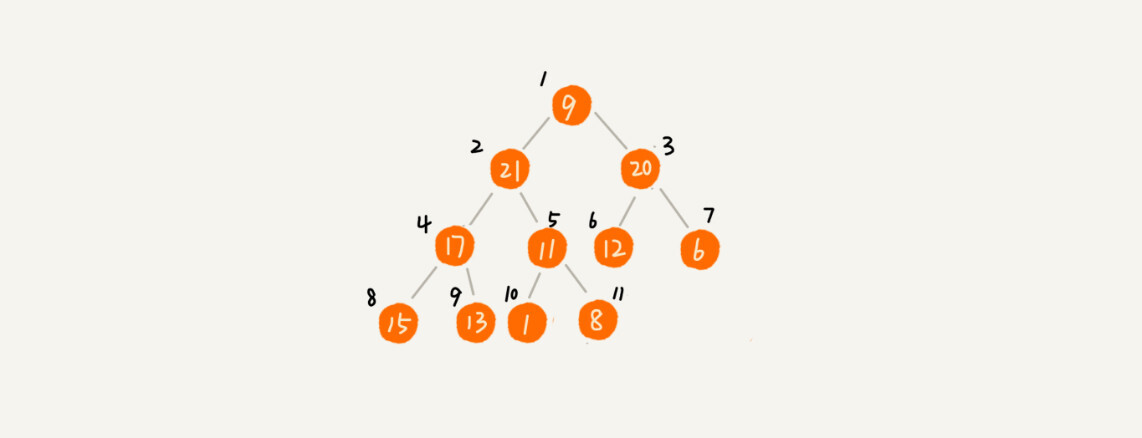
由此我们可以得出一个与下面算法实现息息相关的结论

如果某一个结点存储时在数组中下标为i

它的父节点位置在i/2
它的左子结点位置在2i
它的右子结点位置在2i+1

堆的相关算法

插入元素

过程思路

在数组末尾插入元素，再判断是否符合堆的特点，即是否小于父节点，如果不小于，跟父节点交换，交换直到小于父节点。这个过程称为堆化，且是过程是自下而上的

代码实现

void insert_node(int a[],int val,int cnt)
{
    int i=(cnt+1)/2;	//也可以只用一个变量i
    int j = cnt+1;
    a[j] = val;			//a[cnt+1]=val
    while(a[i]<a[j] && i>0)	//    while(a[i/2]<a[i] && i/2>0)
    {
        swap(a,j,i);			//swap(a,i,i/2)
        i = i / 2;
        j = j / 2;
    }
}
void swap(int a[], int m, int i)
{
    int temp = a[i];
    a[i] = a[m];
    a[m] = temp;

}

删除堆顶元素

过程思路

删除一个元素，由于堆的完全二叉树的特点限制，要提防出现最后一层断层，即不连续。

所以采用的方法是把最末的元素替换堆顶再进行堆化，这样得到的新堆肯定是符合其自身特点的。很明显，这里是从上往下的堆化过程。

代码实现

void heaping_(int a[],int cnt,int i)    //一次该函数调用,可以把堆从i结点开始到堆底的全部堆化
{
    while (true)
    {
        int maxpos = i;              
        if(a[2 * i] > a[maxpos]&& 2 * i <= cnt)maxpos = 2 * i;  //是否左节点会大于该节点
        if (a[2 * i + 1] > a[maxpos] && 2 * i <= cnt)maxpos = 2 * i + 1;    //是否右节点会大于该节点/左节点,注意这里是maxpos不是i因为右节点可能会大于左节点,
        if(i==maxpos)break;         //如果该节点大于左节点又大于右节点,说明不需要交换堆化跳出循环,
        swap(a,maxpos,i);          //把三个结点中最大的那个,换到结点位置
        i = maxpos;                
    }
}
void delete_node(int a[],int cnt)
{
    if(cnt==0)
    {
        return;
    }
    a[1] = a[cnt + 1];
    cnt--;
    heaping_(a, cnt, 1);

}

堆排序

过程思路

堆排序分为两个步骤

建堆
排序

为什么会需要建堆呢，因为排序的时候的算法利用了堆的特点，建堆是通过对已经有的数组进行堆化，使数组满足堆的特点。这里采用的是：从最后一个非叶子结点——>也就是数组有效元素/2位置开始堆化(叶子节点不需要堆化，)

排序的思想是每次都将大顶堆堆顶元素放在数组末尾，再对数组里n-2个元素进行堆化，多次进行直到把倒数第二个元素进行交换，堆化。

代码实现

void build_heap(int a[],int cnt)    //采用的方法是从下往上依次堆化
{
    int i;
    int maxpos;
    for (i = cnt / 2; i>0;i--)
    {
        heaping_(a,cnt,i);
    }
}
void sort_heap(int a[], int cnt)
{
    int i = cnt;
    while (i > 1)
    {
        swap(a, 1, i);
        i--;
        heaping_(a, i, 1);
    }
}

完整代码

#include <stdio.h>
#include <stdbool.h>
#include <windows.h>
#include <malloc.h>
int cnt;
void heaping_(int a[], int cnt, int i);
void build_heap(int a[],int cnt);       //大顶堆
void sort_heap(int a[],int );             //堆排序
void insert_node(int a[],int val,int cnt);  //插入一个元素
void delete_node(int a[],int cnt); //删除堆顶元素
void swap(int a[], int m, int n);
void print_node(int a[],int cnt)
{
    int i;
    for (i = 1; i <=cnt; i++)
    {
        printf("%d  ", a[i]);
    }
}

int main()
{
    int cnt = 8;
    int heap[10] ={0,7,5,19,8,4,1,20,13};
    build_heap(heap,cnt);
    print_node(heap,cnt);
    printf("\n");
    //插入
    printf("after inserting:");
    printf("\n");
    insert_node(heap, 27, cnt);
    print_node(heap, cnt);
    //删除
    printf("\n");
    printf("after deleting");
    delete_node(heap, cnt);
    cnt--;
    printf("\n");
    print_node(heap, cnt);
   //堆排序
    printf("\n");
    printf("after sorting");
    printf("\n");
    sort_heap(heap, cnt);
    print_node(heap, cnt);

}

void heaping_(int a[],int cnt,int i)    //一次该函数调用,可以把堆从i结点开始到堆底的全部堆化
{
    while (true)
    {
        int maxpos = i;
        if (2 * i <= cnt && a[2 * i] > a[i])
            maxpos = 2 * i;                                                 //是否左节点会大于该节点
        if (2 * i +1<= cnt && a[2 * i + 1] > a[maxpos])
            maxpos = 2 * i + 1;     //是否右节点会大于该节点/左节点,注意这里是maxpos不是i因为右节点可能会大于左节点,
        if(i==maxpos)break;         //如果该节X点大于左节点又大于右节点,说明不需要交换堆化跳出循环,
        swap(a,maxpos,i);          //把三个结点中最大的那个,换到结点位置
        i = maxpos;                
    }
}
void build_heap(int a[],int cnt)    //采用的方法是从下往上依次堆化
{
    int i;
    int maxpos;
    for (i = cnt / 2; i>0;i--)
    {
        heaping_(a,cnt,i);
    }
}
void sort_heap(int a[], int cnt)
{
    int i = cnt;
    while (i > 1)
    {
        swap(a, 1, i);
        i--;
        heaping_(a, i, 1);
    }
}

void swap(int a[], int m, int i)
{
    int temp = a[i];
    a[i] = a[m];
    a[m] = temp;

}
void insert_node(int a[],int val,int cnt)
{
    int i=cnt+1;
    a[i] = val;
    while(a[i]>a[i/2] && i/2>0)
    {
        swap(a,i,i/2);
        i = i / 2;
    }
}
void delete_node(int a[],int cnt)
{
    if(cnt==0)
    {
        return;
    }
    a[1] = a[cnt];
    cnt--;
    heaping_(a, cnt, 1);
}

运行结果如下
在这里插入图片描述