质数相关问题（判定、分解、筛选）

质数定义

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。

---

质数的判定——试除法

模板代码

bool is_prime(int x)       //判断x是不是质数
{
    if(x<2)     //如果x小于2，那x肯定不是质数
        return false;
    for(int i=2;i<=x/i;i++)    //从2遍历到x/i的所有数
        if(x%i==0)  //如果能找到x将它整除的
            return false;   //那肯定也不是质数
    return true;  //过程中一直没找到，则返回true
}

原理

如果存在$d$整除$n$，那么必然存在$\frac{n}{d}$整除$n$
$d$和$\frac{n}{d}$是成对出现的，所以没必要从$2$到$n$将它们都遍历一遍
所以只要遍历$d\le \frac{n}{d}$的部分就行了，化简得$d\le \sqrt{n}$
所以写成

for(int i=2;i<=x/i;i++)

为什么不写成下面的形式？

• for(int i=2;i<=sqrt(n);i++)
  $sqrt(n)$的执行速度比较慢，而且这么写的话，循环每次执行都会执行一遍，速度更慢了
• for(int i=2;i*i<=n;i++)
  当n接近int型数据的上限时，很可能因此i的溢出，不建议用

时间复杂度

$O(\sqrt{n})$

---

分解质因数——试除法

定义解释

把一个合数分解成若干个质因数的乘积的形式，即求质因数的过程叫做分解质因数。
分解质因数只针对合数。（分解质因数也称分解素因数）求一个数分解质因数，要从最小的质数除起，一直除到结果为质数为止。

任何正整数皆有独一无二的质因子分解式 。只有一个质因子的正整数为质数。

每个合数都可以写成几个质数（也可称为素数）相乘的形式，这几个质数就都叫做这个合数的质因数。如果一个质数是某个数的因数，那么就说这个质数是这个数的质因数；而这个因数一定是一个质数。

举例：

1没有质因子。
5只有1个质因子，5本身。（5是质数）
6的质因子是2和3。(6 = 2 × 3)
2、4、8、16等只有1个质因子：2。（2是质数，4 =2²，8 = 2³，如此类推）
10有2个质因子：2和5。(10 = 2 × 5)

质因数的底数和指数：

在一个数的质因子分解式中，出现的质数本身的值为底数，它出现的次数称为指数

原理

算数基本定理：任何一个大于 1 的自然数 n，如果 n 不为质数，那么 n 可以唯一分解成有限个质数的乘积：

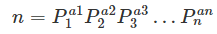
这里 $P1<P2<P3<\cdots <Pn$均为质数，其中指数 $a_i$是正整数。
特别要注意——分解质因数与质因数不一样，分解质因数是一个过程，而质因数是一个数。
一个合数分解而成的质因数最多只包含一个大于$\sqrt{n}$的质因数。
（反证法，若 n可以被分解成两个大于$\sqrt{n}$ 的质因数，则这两个质因数相乘的结果大于 n，与事实矛盾）
当枚举到某一个数 $i$ 的时候，$n$ 的因子里面已经不包含 $[2,i-1]$里面的数（已经被除干净了），如果 $i|n$，则 i 的因子里面也已经不包含 $[2,i-1]$ 里面的数，因此每次枚举的数都是质数。
质因子（质因数）在数论里是指能整除给定正整数的质数。根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。
两个没有共同质因子的正整数称为互质。因为 1没有质因子，1与任何正整数（包括 1本身）都是互质。
只有一个质因子的正整数为质数。

模板代码

//题目背景：AcWing 867 分解质因数
void divide(int x)
{
    for(int i=2;i<=x/i;i++) //数x的质因数中比根号x大的最多只可能有一个
    {                         //所以这里先遍历到根号x
        if(x%i==0)   //看上去是遍历了数x的所有因子，其实不然，原理见上面
        {
            int s=0;   //s记录指数
            while(x%i==0)
            {
                x/=i;
                s++;
            }
            printf("%d %d\n",i,s);
        }
    }
    if(x>1) printf("%d %d\n",x,1);   //对可能出现且仅有一个的大于根号x的质因子进行特判，如果存在，一定是最后一个，看它是等于1还是大于1，大于1就肯定是
    printf("\n");
}

时间复杂度

$O(logn)$~$O(\sqrt{n})$之间
平均为$O(\sqrt{n})$

---

筛质数

问题背景

给定一个正整数 n，请你求出 1∼n 中质数的个数。
我们首先考虑这样一个事，一个数如果是质数，那他的倍数一定是合数，我们根据这一结论筛掉不必要的判断。

朴素筛法

• 步骤：把 $[2,n-1]$ 中的所有的数的倍数都标记上，最后没有被标记的数就是质数
• 原理：假定有一个数 $p$ 未被 $[2,p-1]$中的数标记过，那么说明，不存在 $[2,p-1]$中的任何一个数的倍数是 $p$，也就是说$[2,p-1]$中不存在 $p$ 的约数，因此，根据质数的定义可知：$p$是质数
• 调和级数:当$n$趋近于正无穷的时候，$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{n}=lnn+c$（c 是欧拉常数，约等于0.577左右）
• 时间复杂度：约为 $O(nlogn)$（注：此处的$log$特指以$2$为底）

void get_primes2(){
    for(int i=2;i<=n;i++){

        if(!st[i]) primes[cnt++]=i;//把质数存起来
        for(int j=i;j<=n;j+=i){//不管是合数还是质数，都用来筛掉后面它的倍数
            st[j]=true;
        }
    }
}

埃式筛法（对朴素筛法进行了优化）

埃式筛法的思路非常简单，就是用已经筛选出来的素数去过滤所有能够被它整除的数。这些素数就像是筛子一样去过滤自然数，最后被筛剩下的数自然就是不能被前面素数整除的数，根据素数的定义，这些剩下的数也是素数。

• 质数定理：$1～n$中有$\frac{n}{lnn}$个质数

• 步骤：在朴素筛法的过程中只用质数项去筛

• 时间复杂度：$O(nlog(logn))$

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉
                    //0表示没被筛掉，1表示被筛掉了
void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;  //如果为真，说明被筛掉了
        primes[cnt ++ ] = i;  //记录下质数
        for (int j = i + i; j <= n; j += i)   //把它的倍数都给筛掉
            st[j] = true;
    }
}

线性筛法

• 若$n\approx 10^6$，线性筛和埃氏筛的时间效率差不多，若$n\approx 10^7$，线性筛会比埃氏筛快了大概一倍。
• 核心：$1～n$内的合数 $p$只会被其最小质因子筛掉。（算数基本定理）
• 原理：$1～n$之内的任何一个合数一定会被筛掉，而且筛的时候只用最小质因子来筛，然后每一个数都只有一个最小质因子，因此每个数都只会被筛一次，因此线性筛法是线性的.
• 枚举到 i 的最小质因子的时候就会停下来，即if (i % primes[j] == 0) break;
• 当 i % primes[j] != 0时，primes[j] 一定小于 i 的最小质因子，而primes[j]又一定小于 i 且 primes[j] 是 primes[j] 的最小质因子，primes[j] 一定是 primes[j]*i 的最小质因子.
• 当 i % primes[j] == 0 时，primes[j] 一定是 i 的最小质因子，而 primes[j] 又是 primes[j] 的最小质因子，因此 primes[j] 是 primes[j]*i的最小质因子.

  int primes[N], cnt; // primes[]存储所有素数
  bool st[N];         // st[x]存储x是否被筛掉

  void get_primes(int n)
  {
      for (int i = 2; i <= n; i ++ )
      {
          if (!st[i]) primes[cnt ++ ] = i;
          // j < cnt 不必要，因为 primes[cnt - 1] = 当前最大质数
          // 如果 i 不是质数，肯定会在中间就 break 掉
          // 如果 i 是质数，那么 primes[cnt - 1] = i，也保证了 j < cnt
          for (int j = 0; primes[j] <= n / i; j ++ )
          {
              st[primes[j] * i] = true;
              if (i % primes[j] == 0) break;  //跳出来是为了保证prime[j]≤i的最小质因子
          }     //因为j是从头开始遍历的，所以会遍历2到（i的最小质因子）等的这些质数
      }
  }

附加小知识

只有形如$6n-1$和$6n+1$的自然数可能是素数，这里的n是大于等于1的整数。
这个定理乍一看好像很高级，但其实很简单，因为所有自然数都可以写成$6n,6n+1,6n+2,6n+3,6n+4,6n+5$这6种，其中$6n,6n+2,6n+4$是偶数，一定不是素数。$6n+3$可以写成$3(2n+1)$，显然也不是素数，所以只有可能$6n+1$和$6n+5$可能是素数。$6n+5$等价于$6n-1$，所以我们一般写成$6n-1$和$6n+1$。