重点考察知识点汇总
- 协方差矩阵

- 协方差矩阵为对称矩阵
- 协方差矩阵的对角线为各分量的方差,其余位置 ( i , j ) (i,j) (i,j)表示的是分量 i i i和分量 j j j的协方差
-
多元正态分布的线性组合仍然服从多元正态分布
设 X ∼ N p ( μ , Σ ) X\sim N_{p}(\mu,Σ) X∼Np(μ,Σ), B B B为 s × p s\times p s×p常数矩阵, d d d为 s s s维常向量,令 Z = B X + d Z=BX+d Z=BX+d,则 Z ∼ N s ( B μ + d , B Σ B T ) Z\sim N_{s}(B\mu+d,BΣB^{T}) Z∼Ns(Bμ+d,BΣBT) -
多元条件正态分布

学会分块 -
两个随机向量相互独立的充分必要条件
协方差为0 -
协方差的性质

-
正交矩阵的性质:该矩阵的转置 等于 该矩阵的逆矩阵
-
转置的性质:

-
多元正态分布 μ μ μ, Σ Σ Σ的最大似然估计公式
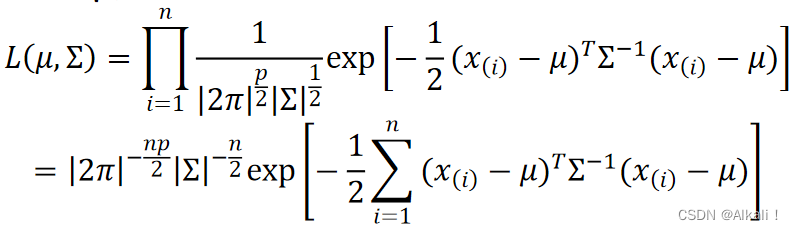

-
常用矩阵微分

-
极大似然估计函数 取对数后 再分别对 μ μ μ和 Σ Σ Σ求微分的结论
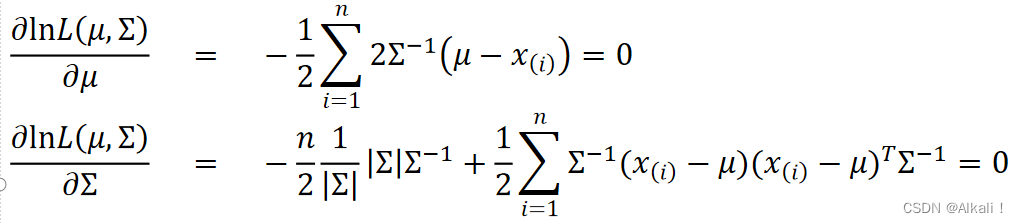
2-1
题目

理论基础
设 X ∼ N p ( μ , Σ ) X\sim N_{p}(\mu,Σ) X∼Np(μ,Σ), B B B为 s × p s\times p s×p常数矩阵, d d d为 s s s维常向量,令 Z = B X + d Z=BX+d Z=BX+d,则 Z ∼ N s ( B μ + d , B Σ B T ) Z\sim N_{s}(B\mu+d,BΣB^{T}) Z∼Ns(Bμ+d,BΣBT)
具体解题
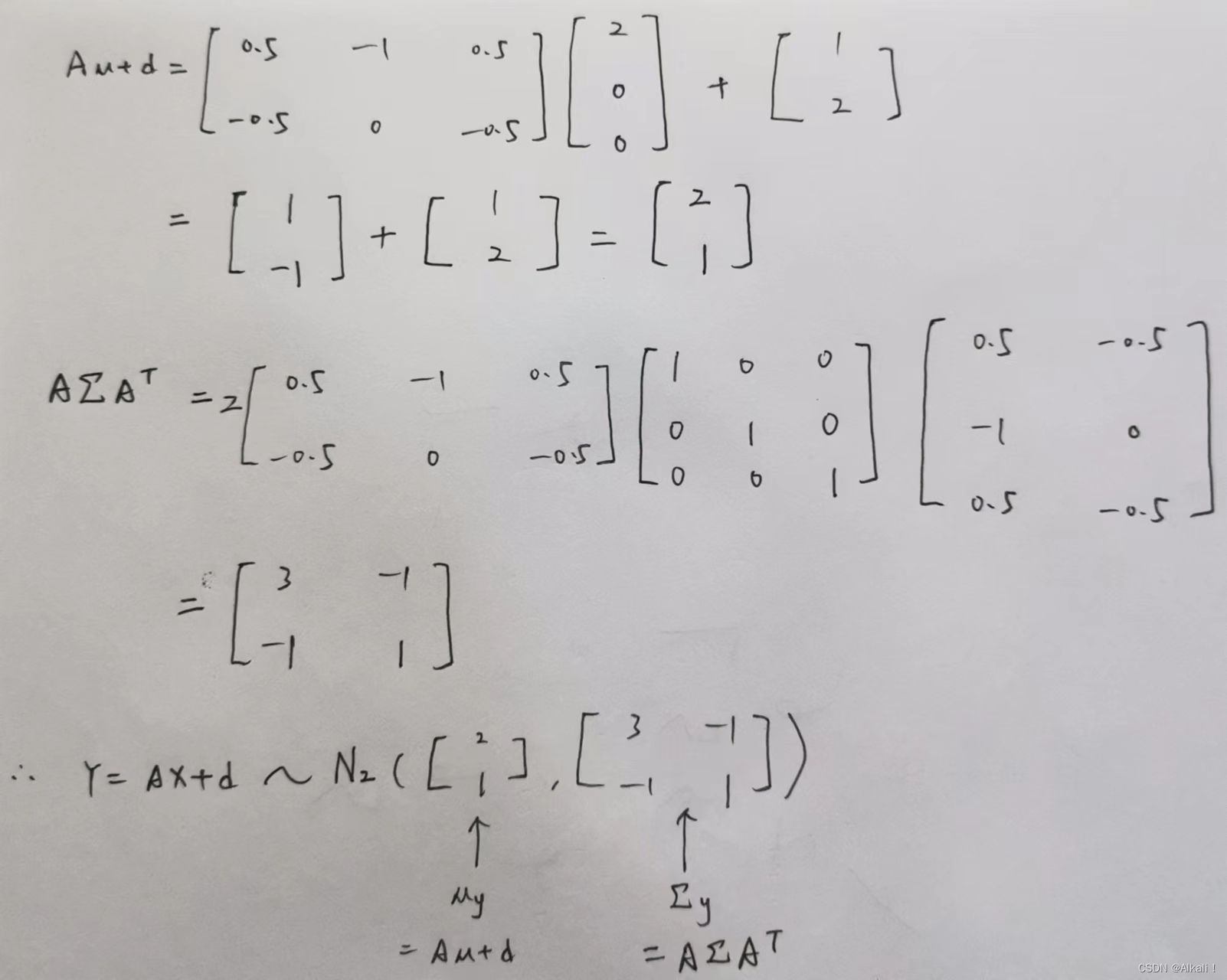
2-4
题目

理论基础

协方差矩阵的性质:

- 协方差矩阵为对称矩阵
- 协方差矩阵的对角线为各分量的方差
具体解题
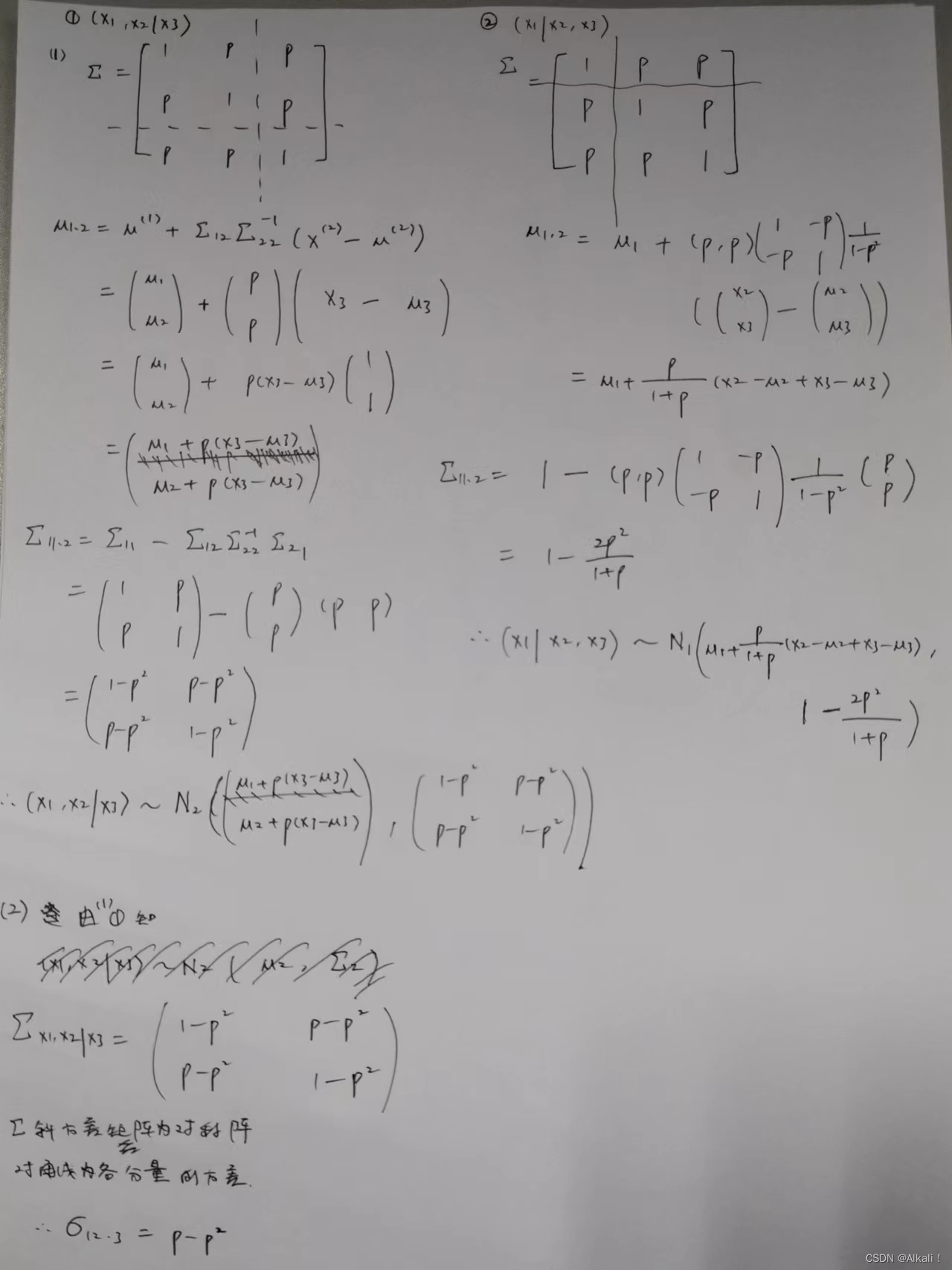
2-6
题目

理论基础
- 设 X ∼ N p ( μ , Σ ) X\sim N_{p}(\mu,Σ) X∼Np(μ,Σ), B B B为 s × p s\times p s×p常数矩阵, d d d为 s s s维常向量,令 Z = B X + d Z=BX+d Z=BX+d,则 Z ∼ N s ( B μ + d , B Σ B T ) Z\sim N_{s}(B\mu+d,BΣB^{T}) Z∼Ns(Bμ+d,BΣBT)
- 两个随机向量相互独立 ⟺ \Longleftrightarrow ⟺ 他们的协方差(矩阵)为 0 0 0矩阵
- 协方差的性质

具体解题
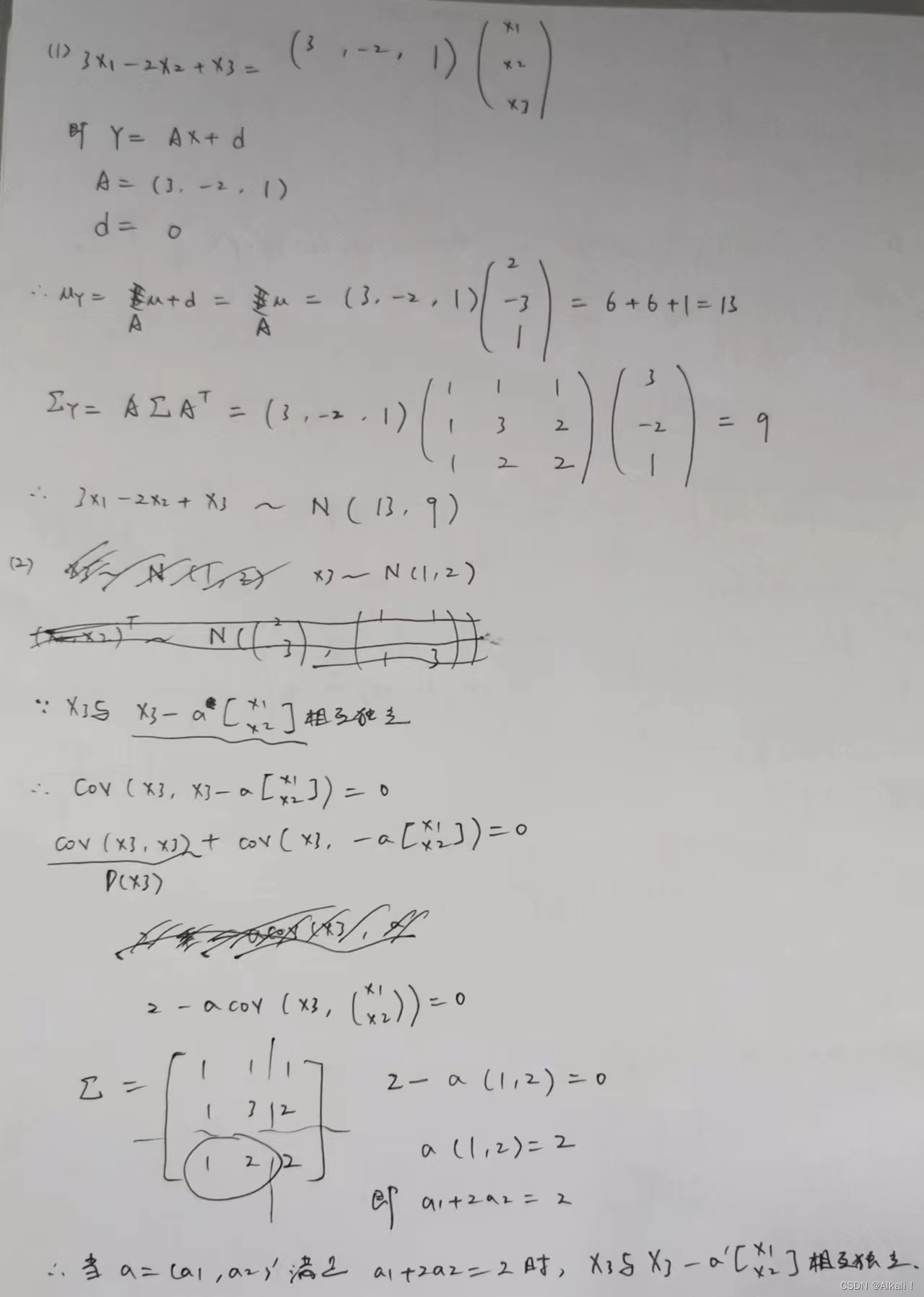
2-9
题目

理论基础
- 正交矩阵的性质:该矩阵的转置 等于 该矩阵的逆矩阵
- 设 X ∼ N p ( μ , Σ ) X\sim N_{p}(\mu,Σ) X∼Np(μ,Σ), B B B为 s × p s\times p s×p常数矩阵, d d d为 s s s维常向量,令 Z = B X + d Z=BX+d Z=BX+d,则 Z ∼ N s ( B μ + d , B Σ B T ) Z\sim N_{s}(B\mu+d,BΣB^{T}) Z∼Ns(Bμ+d,BΣBT)
- 转置的性质:

- 两个随机向量相互独立 ⟺ \Longleftrightarrow ⟺ 他们的协方差(矩阵)为 0 0 0矩阵
- 协方差矩阵的性质

- 协方差矩阵为对称矩阵
- 协方差矩阵的对角线为各分量的方差
具体解题
第一小问略 算一下即可
第二小问:
证明一:

证明二:
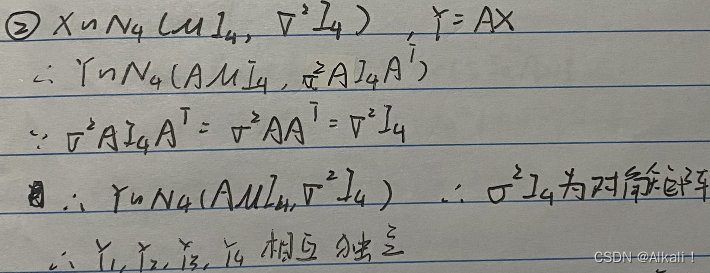
证明三:

2-15
题目
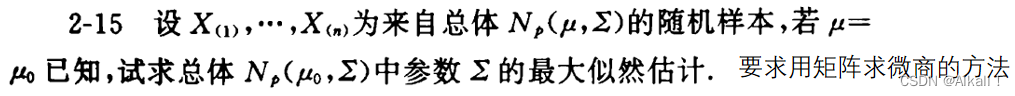
理论基础
- 多元正态分布
μ
μ
μ,
Σ
Σ
Σ的最大似然估计公式
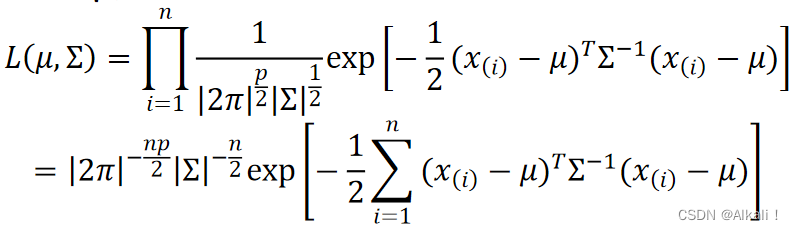

- 常用矩阵微分

- 极大似然估计函数 取对数后 再分别对
μ
μ
μ和
Σ
Σ
Σ求微分的结论
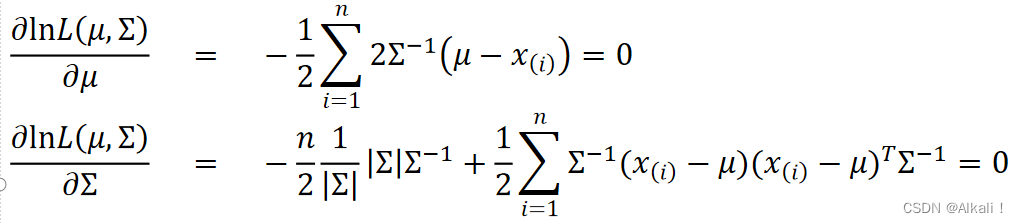
具体解题
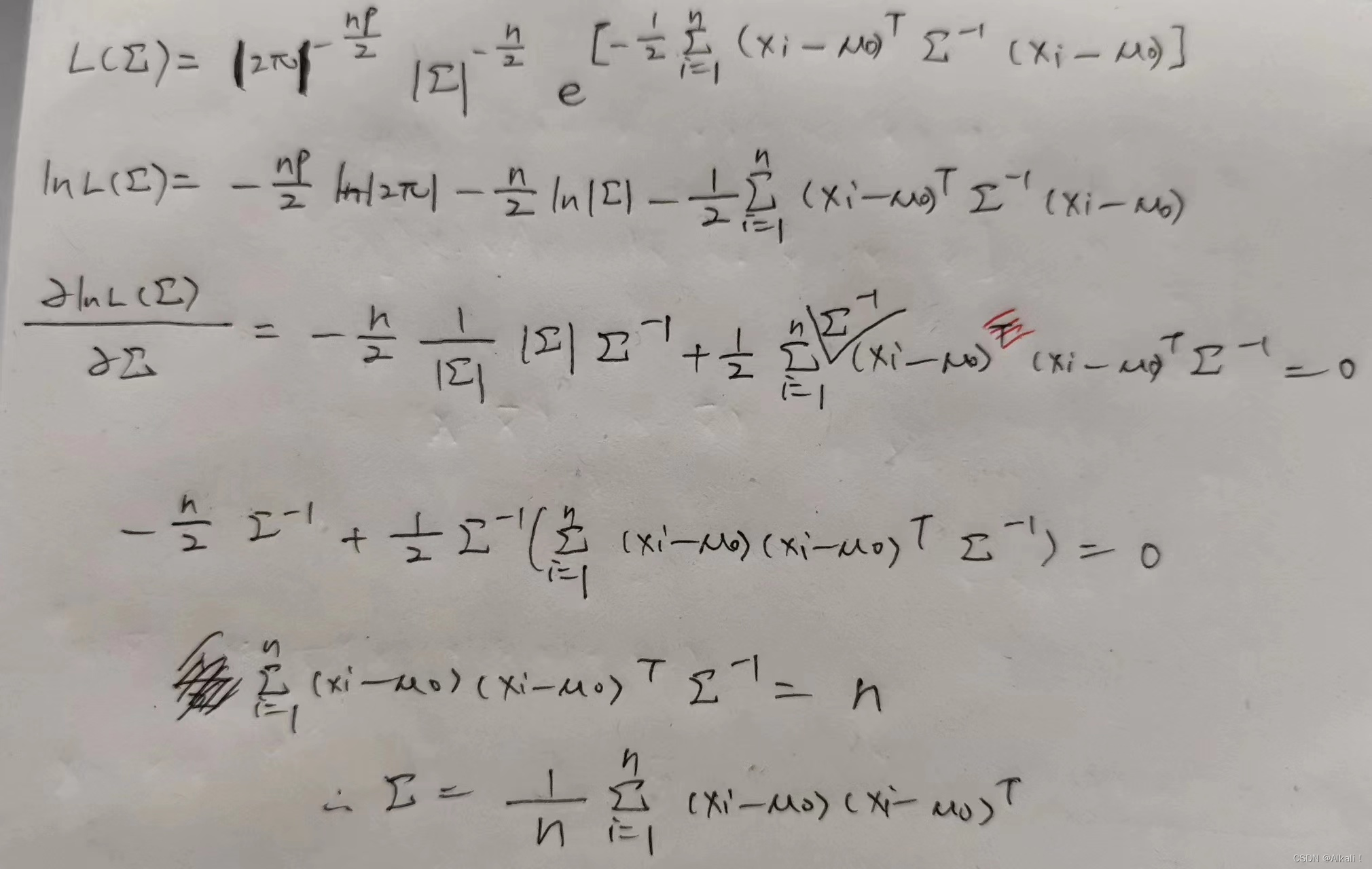








 本文探讨了多元正态分布的基本理论及其线性变换特性,重点介绍了协方差矩阵的性质,包括其对称性及对角线元素含义,并讨论了随机向量独立性的充分必要条件。此外,还讲解了正交矩阵的性质及其应用。
本文探讨了多元正态分布的基本理论及其线性变换特性,重点介绍了协方差矩阵的性质,包括其对称性及对角线元素含义,并讨论了随机向量独立性的充分必要条件。此外,还讲解了正交矩阵的性质及其应用。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










