一篇看懂归并排序MergeSort算法与代码

原理

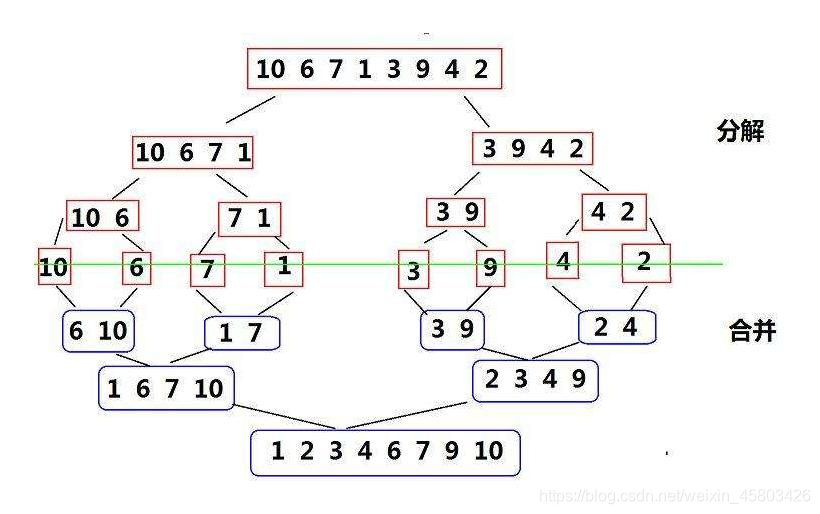
归并排序（MergeSort）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序是稳定的排序算法。

作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法组合实现：
自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
自下而上的迭代；

算法步骤：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

4. 重复步骤 3 直到某一指针达到序列尾；

5. 将另一序列剩下的所有元素直接复制到合并序列尾。
   

代码实现

    public static void mergeSort(int[] array) {
        mergeRangeSort(array, 0, array.length);
    }

    private static void mergeRangeSort(int[] array, int from, int to) {
        int size = to - from;
        if (size <= 1) {
            return;
        }

        int mid = from + (to - from) / 2;

        mergeRangeSort(array, from, mid);
        mergeRangeSort(array, mid, to);

        merge(array, from, mid, to);
    }

    private static void merge(int[] array, int from, int mid, int to) {
        int size = to - from;
        int[] newArray = new int[size];

        int idx1 = from;
        int idx2 = mid;
        int index = 0;

        while (idx1 < mid && idx2 < to) {
            if (array[idx1] <= array[idx2]) {
                newArray[index++] = array[idx1++];
            } else {
                newArray[index++] = array[idx2++];
            }
        }
        if (idx1 < mid) {
            while (idx1 < mid) {
                newArray[index++] = array[idx1++];
            }
        } else {
            while (idx2 < to) {
                newArray[index++] = array[idx2++];
            }
        }

        for (int i = 0; i < size; i++) {
            array[from + i] = newArray[i];
        }
    }

代码分析

性能分析

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。

时间复杂度：
因为快速排序一直在利用中间下标将区间递归分为左右两个小区间，图解像一个二叉树，所以二叉树的深度可以形象的比作快速排序要执行的次数。一直从中间下标递归分割固定的区间长度为完全二叉树时，深度最低时，时间复杂度最小为O(log(n))。再从开始到结束下标将其中的所有元素覆盖到旧组中时间复杂度为O(n)，合起来就是O(nlog(n))。
空间复杂度：
归并排序归并过程需要创建新数组，新数组的长度和传入的数组长度一样，所以其需要占用n个额外空间。
归并排序和快速排序是唯二的空间复杂度不是O(1)的排序算法。

稳定性

归并排序是稳定的排序算法。